Оптимизация машинного парка

Имеются m типов машин в количествах d ₁ ,…, d_m и видов работ, подлежащих выполнению в объёмах 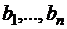. Задана матрица 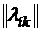, где 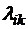– производительность i -й машины на k -й работе, матрица 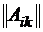, где 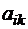– себестоимость выполнения единицы k -й работы машиной i -го типа и стоимость 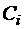одной машины i -го типа.

Составить математическую модель задачи по определению оптимального машинного парка (т.е. количество машин каждого типа) и оптимального его распределения по указанным работам из условия минимизации суммарной стоимости (машинного парка и произведенных работ).

Задача оптимального планирования

Имеется фирма в составе двух предприятий, производящих соответственно два и четыре различных вида продукции. Каждое предприятие для производства продукции использует свои внутренние, локальные ресурсы (рабочую силу и оборудование). Предприятия совместно потребляют некоторый лимитированный ресурс (сырьё). Пусть b − количество общего ресурса, b ₁, b ₂ – ресурсы первого предприятия, b ₃, b ₄ − ресурсы второго предприятия, a _ij − количество i -го ресурса, необходимое для производства j -го вида продукции, С _i − прибыль фирмы от реализации единицы i -й продукции.

Определить план производства продукции, дающий максимальную прибыль.

Задача распределения удобрений

Имеется ограниченное количество удобрений К, которое необходимо распределить между посевами n различных с/х культур. Суммарная площадь посева фиксирована S. Известны: 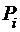– цена реализации единицы продукта, 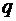– цена единицы удобрений. Урожайность 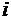-ой культуры зависит от количества внесенных на единицу площади удобрений. Продукция должна быть получена во вполне определенном ассортименте .

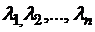Найти способ распределения земель и удобрений, при котором суммарный доход от продажи продукта будет максимален.

Задача загрузки станков

Ткацкая фабрика располагает N ₁станками первого типа и 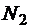станками второго типа. Станки могут производить три вида тканей: 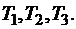Каждый вид станка может производить любой из видов ткани, но в неодинаковом количестве. Станок первого типа производит в единицу времени 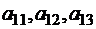метров ткани 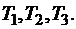соответственно, станок второго типа 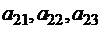метров ткани. Каждый метр ткани 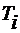– приносит прибыль 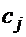, 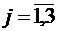. Согласно плану производства фабрика должна произвести в единицу времени не менее 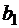метров ткани 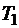, не менее 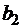метров ткани 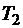и не менее 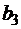метров ткани .

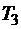Требуется распределить загрузку станков производством тканей различного вида так, чтобы план был выполнен и при этом прибыль в единицу времени была максимальна.