Фабрика может производить n различных продуктов, располагая для этого m видами ресурсов в количестве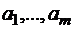 
. Для производства продуктов могут быть использованы S технологических способов. Заданы величины 
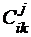, характеризующие нормы расхода i -го ресурса на единицу k -го продукта при изготовлении его j -м способом. Известна цена P k единицы k -го продукта. Составить модель задачи по определению оптимального набора продуктов и способов их производства из условия максимизации товарной продукции при дополнительном условии, согласно которому любой k -й продует либо должен производиться в количестве, не меньшем d k, либо совсем не производиться.
Задача о распределении устройств
Предприятие планирует ремонт технических устройств в количестве n штук в трех мастерских. Затраты на ремонт технических устройств в различных мастерских различны, время ремонта различно. Средства на ремонт огра-ничены.
Составить план распределения технических устройств по мастерским так, чтобы суммарное время на ремонт было минимально.
Производственная программа и план перевозок
Четыре предприятия могут производить продукцию в урочное время в количествах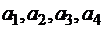 
и дополнительно в сверхурочное время в количествах 
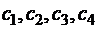. При этом затраты на производство единицы продукции по предприятиям составляют 
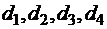при работе в урочное время и соответственно на 50 % выше при работе в неурочное время. Продукция должна быть доставлена четырём потребителям в количествах 
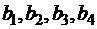. Транспортные расходы за перевозку единицы продукции от i -го предприятия k -му потребителю заданы матрицей 
.
Определить оптимальную производственную программу предприятий и оптимальный план перевозок.
Задача размещения модулей на плате
Пусть размещению на плате подлежат n модулей. По известной принципиальной схеме определяется матрица связей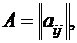 
где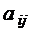 
– число связей между i- м и j -м модулями. Все n модулей должны быть размещены на плате, разбитой на m > n позиций. Задана матрица 
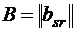стоимостей "прокладки" одной линии связи между любыми модулями, размещёнными в позициях S и r.
Составить модель размещения модулей на плате, минимизирующую суммарную стоимость связей.
Распределение задач между узлами АСУ
АСУ, состоящая из m узлов, решает задачи n типов. Пусть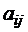 
– затраты на решение i – задачи в j -м узле, 
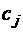– допустимые затраты в j -м узле, 
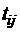– время, необходимое для решения i -й задачи в j – узле, p i – допустимое время решения i -й задачи.
Оптимизировать распределение задач (поставить две оптимизационные задачи).
