Кодтық қашықтық - бұл кез-келген кодтық комбинация басқасынан ажыратылатын элементтердің минималды саны. Мысалы, код мынандай комбинациялардан тұрады: 1011, 1101, 1000 және 1100. Бірінші екі комбинацияны салыстыра отырып d=2 табамыз. Ең үлкен шама d=3 бірінші және төртінші комбинацияларын салыстырғанда табылады, ал ең кішісі d=1 екінші және төртінші, үшінші және төртінші комбинацияларды салыстырғанда табылады. Үш өлшемді кубта бір-бірінен d=3-ке ажыратылатын кодтық белгілері бар шыңдарды таңдайық. Бұндай шыңдар кубтың кеңістік диагоналдарының ұштарында орналасады. Олар тек төрт жұпты болады: 000 және 111, 001 және 110, 100 және 011, 010 және 101. Осындай ережемен жасалған код дара қатені түзете алады немесе екі дара қатені таба алады.
Кодтың түзету қабілеті кодтық қашықтыққа байланысты: а) d=1 кезінде қате табылмайды; б) d=2 кезінде дара қателер табылады; в) d=3 кезінде дара қателер түзетіледі немесе екілік қателер табылады. Жалпы жағдайда
, (1)
мұндағы d - минималды кодтық қашықтық, r - табылған қателер саны,
s - түзетілген қателер саны. Сонымен r≥s қажетті шарт болып табылады.
Түзетуші кодтар қатені табуға және оны жөндеуге мүмкіндік береді, сондықтан бұл кодтарды қолдану – ақпаратты бөгетпен дискретті каналдар бойынша жіберудің сапасын жоғарлату тәсілінің бірі. Шеннон теоремасына сәйкес аз өткізгішті қабілетке ие, ақпаратты жіберу жылдамдығы кезінде, ақпаратты қателіксіз жіберуді қамтамасыз ететін, код бар болады. Қазіргі уақытта табатын және барлық емес тек жарты қатені жөндейтін, кодтар қолданылуда.
Егер бастапқы алфавит көлемі 
құрса, онда барлық мүмкін кодтық комбинацияның n ұзындықты жалпы санынан 
дискретті ақпаратты жіберу үшін барлығы емес, тек қана қажет саны ғана қолданылады. Қабылдауда қатені табу (жөндеу) үшін келесі шартты орындау керек:
| (4.15) |
Егер 
онда барлық n-ші элеметтік кодтың мүмкін тізбегі жіберу үшін қолданылады және рұқсат етілген болып табылады. Бұндай тәсілмен табылған код қарапайым деп аталады, ол қатені табуға және жөндеуге қабілетті емес. Қателікті табу және оны жөндей алуы үшін, теңсіздігін орындау керек. Сонымен қоса саны(
) тең, қолданылмаған n-ші элеметті код комбинациясы рұқсат етілмеген деп аталады, яғни олар байланыс каналы бойынша жіберіле алмайды және олардың қабылдаушы жақта пайда болуы қателікке алып келеді.
Рұқсат етілмеген кодтық комбинациялар кодтың артықшылығын анықтайды. Кодтық комбинацияда қателік табылады, егер жіберілген рұқсат етілген комбинация рұқсат етілмегендердің біреуінен өтсе. Рұқсат етілген кодтық комбинация 
ретінде, бір бірінен максималды ерекшеленетіндерін таңдау керек. Кез келген түзетуші код артықшылықты (артық, қажет емес комбинацияға ие) код болып табылады.
Түзетуші кодты бейнелеу үшін келесі параметрлер енгізіледі:
1) Хэмминг қашықтығы d кодтық комбинация арасындағы айырым дәрежесін көрсетеді. Кез келген екілік кодтық комбинация үшін бұл қашықтық оларда сәйкес келмейтін разряд санына тең. Хэмминг қашықтығы математикалық осы кодтық комбинацияның бірлік санының екілік модуль бойынша суммасы ретінде есептелінеді.
2) Кодтық комбинация салмағы W оған кіретін нөлдік символдың санына тең. Сондықтан Хэмминг қашықтығы – бұл модуль бойынша салмақ суммасы
3) Кодтық қашықтық do– бұл берілген код үшін минималды Хэмминг қашықтығы. Барлық мүмкін кодты комбинация жұбын таңдап алып және олар үшін d есептеп, олардың ішінен минималдыны табу керек, бұл кодтық қашықтық болады. Рұқсат етілген кодтық комбинация ретінде бір бірінен максималды ерекшеленетіндерін, таңдау керек.
4) Кодтың түзетушілік қабілеттігі табылған және жөнделген қателіктің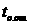 
қысқалығымен анықталады, ол дегеніміз кодтық комбинацияда табылған немесе артқы кодпен жөнделген қателік санына кепілдемемен түсіндіріледі. Қысқашалық үлкен болған сайын жетілдірілген код болып табылады. 
кодты қашықтықты кодтар үшін және әрі қарай қысқаша 
Кодтық арақашықтықпен түзетуші қателіктің қысқалығы арасындағы байланыс теңдеумен анықталады:
 жұп үшін 
 тақ үшін 
| (4.16) |
Сонымен берілген түзетуші қабілетті кодты алу тапсырмасы кодтық комбинациянын минималды кодтық қашықтықты алуды қажет ететін, кодтық комбинацияны таңдау тапсырмасына сәйкес келеді. Үлкен n кезінде бұндай таңдау қиын, сондықтан да тәжірибеде берілген 
код алу мақсатымен жинақтауды қажет етпейтін және жүзеге асырудың қабылдауға болатын қиындықтарымен ерекшеленетін, код құрудың кең тараған әдісін алды.
5) Rкқатынасты жылдамдық коды кодтағы рұқсат етілген кодтық комбинацияның қатынасты саның көрсетеді және формуламен есептелінеді:
| (4.17) |
өлшемі кодтың артықшылық коэффициенті деп аталады.
