В результате соответствующих упражнений учащиеся должны понять, что любой квадрат есть прямоугольник, но не любой прямоугольник является квадратом.
Для того чтобы определить, является ли предъявленная фигура прямоугольником, надо проверить два условия:
1) является ли она четырехугольником;
2) все ли углы прямые.
Если данная фигура не является четырехугольником, то второе условие проверять не нужно, можно сразу сделать вывод.
Для того чтобы определить, является ли данная фигура квадратом, надо проверить также два условия: 1) является ли она прямоугольником, 2) все ли стороны равны по длине.
* * *
1. Работа по учебнику.
Задание 1 (с. 80).
Определения прямоугольника и квадрата вводятся после сравнения этих фигур между собой. Дети рассматривают изображения розовой и зеленой фигур (на с. 80 учебника). На вопрос о том, что общего у этих фигур, дети могут ответить так: обе фигуры – многоугольники (это верно); это четырехугольники (тоже верно). Вероятно, учащиеся обратят внимание на углы этих четырехугольников и даже по виду смогут определить, что в каждом четырехугольнике все углы прямые. Если этого не произойдет, учитель должен предложить второклассникам сравнить углы четырехугольников и определить с помощью модели прямого угла, что все углы в обоих многоугольниках – прямые.
Далее выясняются различия четырехугольников. Возможно, дети назовут некоторые несущественные, непринципиальные различия, например, что фигуры различаются цветом: одна – розовая, а другая – зеленая, что розовая фигура больше по размерам, чем зеленая. Реакция учителя: «Все то, что вы назвали, – правильно, но не это главное». Подведите учащихся к мысли о том, что нужно сравнить в каждой фигуре длины сторон. (Предупреждаем: в данном издании учебника длины сторон не выражаются целым числом сантиметров, поэтому советуем производить сравнение с помощью циркуля.) Итак, в результате сравнения учащиеся выяснят, что в розовом четырехугольнике стороны разной длины, а в зеленом все стороны имеют одну и ту же длину (можно сказать по-другому: длины всех сторон равны).
Подведите итоги: «На рисунке изображены два четырехугольника. У каждого из них все углы прямые. Но у зеленого четырехугольника еще и все стороны имеют одну и ту же длину. Этим он отличается от розового четырехугольника».
Далее прочитайте определение прямоугольника, приведенное в учебнике (на с. 80): «Прямоугольником называется такой четырехугольник, у которого все углы прямые».
– Является ли розовая фигура прямоугольником? (Да, так как это четырехугольник и у него все углы прямые.)
– Является ли зеленая фигура прямоугольником? (Да, так как это четырехугольник и у него все углы прямые.)
– Внимательно посмотрите на зеленый прямоугольник. Вам хорошо знакома эта фигура. Как мы ее назвали?
– Значит, квадрат – это прямоугольник, но особый: у него все стороны равны по длине. Прочитайте в учебнике, какая фигура называется квадратом.
Учащиеся читают определение квадрата (на с. 80).
– Итак, знакомимся: квадрат – это прямоугольник.
2. фронтальная работа с классом по демонстрационным таблицам и индивидуальным карточкам.
Задание 1 (по демонстрационной таблице).
– Рассмотрите таблицу на доске.
– Какие фигуры можно назвать прямоугольниками? Почему?
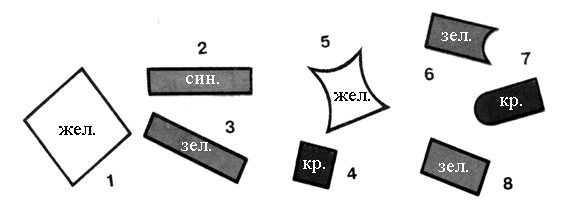
Задание 2 (по карточкам).
– Измерьте длины сторон прямоугольников:

– Назовите прямоугольники, у которых все стороны одинаковой длины. (Фигуры 2, 4.)
– Как называются эти прямоугольники? (Квадраты.)
Задание 2 (по демонстрационной таблице).
– Рассмотрите фигуры на таблице.
– Как называются эти фигуры? (Многоугольники.)
– Посчитайте, сколько углов у каждой фигуры.
– Есть ли среди этих многоугольников прямоугольники?