Адиабатический процесс – это процесс, протекающий в системе, которая не обменивается теплотой с окружающей средой (δ Q = = 0.) Следовательно, 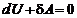 , или
, или  .
.
Уравнения Пуассона:
 ;
;  ;
;  ;
; 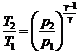 .
.
Работа газа при изопроцессах:
1) изобарический процесс (р = const)
 ;
;
2) изотермический процесс (Т =const)
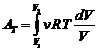 ,
, 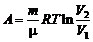 ,
, 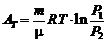 ;
;
3) адиабатический процесс
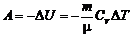
или
 ,
,
где  – показатель адиабаты.
– показатель адиабаты.
Энтропия. Второе начало термодинамики.
Круговой процесс. Цикл Карно
Термический коэффициент полезного действия цикла
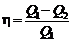 ,
,
где Q 1 – теплота, полученная рабочим теломот нагревателя; Q 2 – теплота, переданная рабочим телом охладителю.
Термический коэффициент полезного действия цикла Карно
 ,
,
где T 1 и T 2 – термодинамические температурынагревателя иохладителя соответственно.
Энтропия термодинамической системы может быть вычислена по формуле Больцмана:
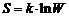 ,
,
где S – энтропия; W – термодинамическая вероятность состояния системы; k – постоянная Больцмана.
Приращение энтропии в процессах идеального газа
 ,
, 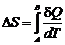 ,
,
где А и В – пределы интегрирования, соответствующие начальному и конечному состояниям системы.
М еханика жидкостей
Коэффициент поверхностного натяжения жидкости равен
 или
или 
где F – сила поверхностного натяжения, действующая на контур, ограничивающий поверхность жидкости; D E – изменение свободной поверхностной энергии пленки жидкости, связанное с изменением площади Δ S поверхности этой пленки.
Формула Лапласа (выражает давление p, создаваемое сферической поверхностью жидкости)
 ,
,
где R – радиус сферической поверхности.
Высота подъема жидкости в капиллярной трубке
 ,
,
где J – краевой угол (J = 0 при полном смачивании стенок трубки жидкостью; J = p при полном несмачивании); R – радиус канала трубки; r – плотность жидкости; g – ускорение свободного падения.
Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями равна
 ,
,
где d – расстояние между плоскостями.
Примеры решения задач
Задача 2.1. Найти импульс m u молекулы водорода при температуре Т = 300 К. Скорость молекулы считать равной средней квадратичной скорости.
| Дано: m = 0,002 кг/моль N A = 6,02×1023 моль -1 Т = 300 К υ = < υ кв> | СИ |
| mυ =? |
Решение.
Масса молекулы водорода

где m– молярная масса, для водорода m = 0,002 кг/моль; N A– постоянная Авогадро, N A = 6,02×1023 моль -1.
Средняя квадратичная скорость молекулы
 .
.
Импульс молекулы равен:

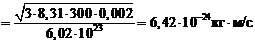 .
.
Ответ:  .
.
Задача 2.2. Определить наиболее вероятную скорость молекул газа, плотность которого при давлении 45кПа составляет 0,38 кг/м3.
| Дано: р = 45 к Па r = 0,38 кг/м3 | СИ 4,5×104 Па
|
| υ в =? |
Решение.
1. Наиболее вероятная скорость молекул газа равна
 , (1)
, (1)
где m– молярная масса, R – молярная газовая постоянная.
2. Плотность газа равна
 , (2)
, (2)
3. Запишем уравнение Менделеева–Клапейрона
 ,
,
откуда с учетом (2) получим
 . (3)
. (3)
4. Подставим (3) в (1), получим
 . (4)
. (4)
5. Подставим в (4) числовые значения:
 .
.
Ответ: υ в = 486,67 м/с.
Задача 2.3. Азот массой m = 7 г при температуре Т 1 = 290 К находится под давлением р 1 = 0,1 МПа. Вследствие изобарного нагревания азот занял объем V 2= 10 л. Найти: 1) объем V 1 газа до расширения; 2) температуру t 2 газа после расширения; 3) плотности газа до и после расширения.
| Дано: µ = 2,8·10-2 кг/моль m = 7·10-3 кг р 1 = 105 Па = const T 1 = 290 К V 2 = 10 л р 2 = р 1 | СИ
10-2 м3 |
| V 1 =?; t 2 =?; ρ1 =?; ρ2 =? |
Решение.
1. Найдем объем газа до расширения, используя уравнение Менделеева–Клапейрона:
 ,
,
отсюда
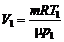 .
.  (1)
(1)
2. Записав уравнение Менделеева–Клапейрона для конечного состояния, найдем температуру Т 2:
 ,
,  ,
,
тогда
 (2)
(2)
3. Подставим в (1), (2) числовые значения
 ;
;
 .
.
4. Плотности газа до и после расширения равны, соответственно:
 ,
,  . (3)
. (3)
5. Подставим в (3) числовые значения:
 ,
,  .
.
Ответ: V 1 = 6,02 л; t 2 = 208 °С; ρ1 = 1,16 кг/м3; ρ2 = 0,7 кг/м3.
Задача 2.4. В баллоне объемом V = 15 л находится аргон под давлением р 1= 600 кПа и температуре Т 1= 300 К. Когда из баллона было взято некоторое количество аргона, давление в баллоне понизилось до р 2 = 400 кПа. Температура в баллоне понизилась до Т 2= = 270 К. Определить массу D m аргона, взятого из баллона.
| Дано: m = 40 г/моль V = 15 л р 1= 600 кПа Т 1= 300 К р 2 = 400 кПа Т 2= 270 К | СИ 40×10-3 кг/моль 15 м3 6∙105 Па
4∙105 Па
|
| D m =? |
Решение:
1.Запишем уравнением Менделеева–Клапейрона для начального и конечного состояния газа:
 (1)
(1)

 (2)
(2)
где m– молярная масса аргона, R – молярная газовая постоянная, R = 8,31 Дж/К×моль.
2. Выразим из (1) и (2) массу аргона в начальном и конечном состояниях, учитывая, что V 1 = V 2 = V:
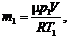
 .
.
3. Найдем искомую массу D m:


Ответ: D m = 37,5 г.
Задача 2.5. В сосуде вместимостью V = 0,3 л при температуре Т = 290 К находится некоторый газ. Считая температуру газа постоянной, Найти, на сколько понизится давление газа в сосуде, если из него из-за утечки выйдет Δ N = 1019 молекул?
| Дано: T = 290 К V = 0,3 л Δ N = 1019 | СИ
3·10-4 м3
|
| Δ р =? |
Решение:
1. Запишем уравнения Менделеева–Клапейрона для начального (до утечки) и конечного (после утечки) состояний газа:
 , (1)
, (1)

 , (2)
, (2)
2. Выразим из уравнений (1) и (2) давления р 1 и р 2 и изменение давления Δ р:
 . (3)
. (3)
3.Так как  , то число молей газа, вытекших из сосуда:
, то число молей газа, вытекших из сосуда:
 . (4)
. (4)
4. С учетом (4) получим из уравнения (3)
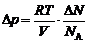 . (5)
. (5)
5. Учитывая, что R = kN A, получим из (5) окончательно
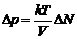 . (6)
. (6)
6. Подставим в (6) числовые значения:

Ответ: ΔР = 133,4 Па.
Задача 2.6. Пылинки массой m = 10-21 кг взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается на 1 % ( ). Считать, что температура во всех слоях воздуха одинаковая и равна Т = 300 К.
). Считать, что температура во всех слоях воздуха одинаковая и равна Т = 300 К.
Дано:
m = 10-21 кг  Т = 300 К
Т = 300 К
| СИ
0,2 м
|
| ∆h =? |
Решение:
1. Поскольку концентрация пылинок равномерно изменяется с высотой h, применим формулу Больцмана
 ,
,
где U – потенциальная энергия частиц, U = = mgh; k – постоянная Больцмана, k = = 1,38×10-23 Дж/К. В итоге получим
 . (1)
. (1)
2. По условию задачи D n << n ( ), поэтому заменим изменение концентрации D n на дифференциал dn. Продифференцируем (1) по h:
), поэтому заменим изменение концентрации D n на дифференциал dn. Продифференцируем (1) по h:
 .
.
3. Так как  , то получим
, то получим
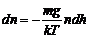 . (2)
. (2)
4. Выразим из (2) искомую толщину слоя:
 . (3)
. (3)
5. Знак минус в (3) показывает, что с увеличением высоты (dh > 0), концентрация молекул падает, поэтому D n < 0. Опустим знак минус (в данной задаче он не существенен) и заменим дифференциалы конечными приращениями:
 . (4)
. (4)
6. Подставим в (4) числовые значения:

Ответ: 
Задача 2.7. В сосуде объемом V = 2 л находятся масса m 1 = 6 г углекислого газа (СО2) и масса m 2 = 5 г закиси азота (N2О) при температуре t = 127 °С. Найти давление смеси в сосуде.
| Дано: V = 2 л m 1 = 6 г µ1 = 4,4·10-2 кг/моль m 2 = 5 г µ2 = 4,4·10-2 кг/моль t = 127 °С | СИ 2 м3 6∙10-3 кг
5∙10-3 кг
400 К
|
| р см =? |
Решение.
1. Согласно закону Дальтона давление смеси газов р см в сосуде равно сумме парциальных давлений:
 . (1)
. (1)
2. Из уравнения Менделеева–Клапейрона вычислим парциальные давления каждого газа:
 ,
,  , (2)
, (2)
 ,
, 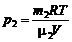 (3)
(3)
3. Подставим (2) и (3) в (1):
 (4)
(4)
4. Подставим в (4) числовые значения:

Ответ: р см = 415 кПа.
Задача 2.8. Кислород массой 320 г нагревают при постоянном давлении от 300 до 310 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа.
| Дано: m= 320 г T 1 = 300 К T 2 = 310 К | СИ 0,32 кг
|
| Q =? ΔU =? A =? |
Решение.
1. Количество теплоты, необходимое для нагревания газа при постоянном давлении, определим из первого начала термодинамики:
 , (1)
, (1)
где Ср – молярная изобарная теплоемкость,  , где i = 5 для кислорода как двухатомного газа; m– молярная масса газа, m= 32 г/моль =
, где i = 5 для кислорода как двухатомного газа; m– молярная масса газа, m= 32 г/моль =  .
.
2. Подставляя в (1) числовые значения, получим
 .
.
3. Изменение внутренней энергии газа
 . (2)
. (2)
4. Подставляя числовые значения и учтя, что  , получим
, получим

5. Работа расширения газа при изобарном процессе:
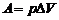 , (3)
, (3)
где  .
.
6. Изменение объема газа при расширении можно найти из уравнения Менделеева–Клапейрона. Для двух состояний газа при изобарном процессе имеем:
 (4)
(4)
 . (5)
. (5)
7. Вычитая почленно (5) из (4), получим:
 (6)
(6)
8. Подставляя (6) в (3), находим:
 . (7)
. (7)
9. Подставим в (7) числовые значения:
А = 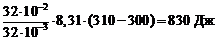 .
.
Ответ: Q = 2908,5Дж, Δ U = 2080Дж, A = 830 Дж.
Задача 2.9. Молярная масса некоторого газа m= 0,03 г/моль, отношение удельных теплоемкостей ср / с V = 1,4. Найти удельные теплоемкости ср и сV.
Дано:
m= 0,03 г/моль

| СИ |
| ср =? сV =? |
Решение.
1. Удельные теплоемкости ср и сV определяются по формулам:
 , (1)
, (1)
 , (2)
, (2)
где m– молярная масса газа; Ср , СV – молярные теплоемкости.
2. Выразим из (1) и (2) молярные теплоемкости:
 , (3)
, (3)
 . (4)
. (4)
3. Связь между молярными теплоемкостями (уравнение Майера)
 , (5)
, (5)
где R – универсальная газовая постоянная.
4. Подставим (3), (4) в (5) и учтем, что  или
или  :
:
 ,
,
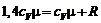 ,
,
 ,
,
 , (6)
, (6)
 . (7)
. (7)
5. Подставим в (6) и (7) числовые значения:

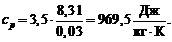
Ответ:  ,
, 
Задача 2.10. Объем V 1= 7,5 л кислорода адиабатически сжимается до объема V 2= 1 л. В конце сжатия устанавливается давление р 2 = 1,6 МПа. Под каким давлением находился газ до сжатия?
| Дано: V 1= 7,5 л V 2= 1 л р 2 = 1,6 МПа | СИ 7,5∙10-3 м3 1,0∙10-3 м3 1,6∙106 Па |
| р 1 =? |
Решение.
1. Согласно уравнению Пуассона
 . (1)
. (1)
гдеg – показатель адиабаты.
Поскольку кислород – двухатомный газ, то для кислородаg = 1, 4.
2. Выразим из (1) давление р 1:
 (2)
(2)
3. Подставим в (2) числовые значения:

Ответ: р 1 = 95,29 кПа.
Задача 2.11. Кислородмассой1 г нагревается от Т 1 = 283 К до Т 2 = 333 К различными способами: а) при р = const; б) при V = = const; в) при Δ Q = 0. Определить изменение внутренней энергии кислорода при его нагревании от Т 1 до Т 2. Газ считать идеальным. Проверить для указанных процессов теоретическое положение о том, что изменение внутренней энергии идеального газа не зависит от процесса перехода, а зависит только от начальной и конечной температуры.
| Дано: Т 1 = 283 К Т 2 = 333 К а) р = const б) V = const в)Δ Q = 0 | СИ |
| Δ U =? |
Решение.
1. Пусть процесс перехода газа из состояния с температурой Т 1 в состояние с температурой Т 2 происходит изобарически (р = const).
2. Согласно первому началу термодинамики
 . (1)
. (1)
3. Количество теплоты, необходимое для нагревания на Δ Т при р = const количества вещества  , равно
, равно
 (2)
(2)
4. Работа газа:
 . (3)
. (3)
5. Используем уравнение Менделеева–Клапейрона для определения изменения объема и температуры:
 (4)
(4)
6. Подставив (4) в (3), а (3) и (2) в (1), а также используя уравнение Майера, получим:
 . (5)
. (5)
7. Рассмотрим случай, когда нагревание газа ведется изохорически (V = const). В этом случае совершаемая газом работа ΔА = 0 и ΔUV = ΔQ. Количество теплоты, необходимое для нагревания на ΔТ (при V = const) количества вещества n = т /m, равно  .
.
Отсюда получим:
 . (6)
. (6)
8. Рассмотрим случай, когда нагревание газа от Т 1 до Т 2 производится адиабатно. В этом случае Δ Q = 0 и Δ U ад = – Δ А. В адиабатном процессе:
 . (7)
. (7)
9. Хотя в адиабатном процессе система тепловой энергии не получает, увеличение температуры газа происходит за счет его сжатия внешними силами. Выражения (5), (6) и (7) идентичны, что подтверждает, что внутренняя энергия идеального газа не зависит от процесса перехода, что и требовалось доказать.
10. Подставим в (5) числовые значения
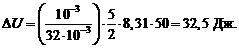
Ответ: Δ U = 32,5 Дж.
Задача 2.12. В четырехтактном двигателе дизеля засосанный атмосферный воздух в объеме 10 л подвергается двенадцатикратному сжатию. Начальное давление – атмосферное, начальная температура 10 °С. Процесс сжатия адиабатный, газ идеальный. Определить конечное давление, конечную температуру и работу сжатия.
| Дано: V 1= 10 л V 1 /V 2 = 12 p 1 = 1 атм t 1 = 10 °С Q = 0 µ = 2, 9 · 10 - 2кг/моль | СИ 10 м3 м/с 105 Па 283 К |
| p 2=? T 2=? А =? |
Решение.
1. Из уравнения адиабаты  определим конечное давление р 2:
определим конечное давление р 2:
 (1)
(1)
2. Из уравнения адиабаты 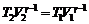 определим Т 2:
определим Т 2:
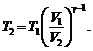 (2)
(2)
3. Допуская, что воздух состоит в основном из кислорода (О2) и азота (N2), можно считать его двухатомным газом с теплоемкостью СV = (5/2) R.
4. Работа при адиабатическом процессе равна
 . (3)
. (3)
5. Подставив (2) в (3), и определив массу воздуха в двигателе из уравнения Менделеева–Клапейрона, получим выражение для работы при адиабатном сжатии:

6. Подставим в (1)–(3) числовые значения и получим:
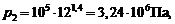


Ответ: р 2 = 3,24·106 Па; Т 2 = 765 К;  .
.
Задача 2.13. Вычислите изменение энтропии одного моля идеального газа при расширении по политропе от объема V 1 до объема V 2. Рассмотрите процессы: а) изотермический; б) адиабатный; в) изобарный.
| Дано: ν = 1 моль V 1, V 2 а) T = const б) Q = 0 в) p = const | СИ |
| Δ S =? |
Решение.
1. Изменение энтропии 1 моля идеального газа при переходе из состояния 1 в состояние 2 можно вычислить по формуле:
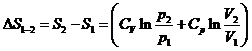 .
.
2. Из уравнения политропического процесса рVn = constможно записать: 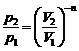 , поэтому
, поэтому
 ,
,
где  .
.
3. При изотермическом процессе n = 1, тогда Ср – пС V = R и  .
.
4. При адиабатном процессе n = γ: Ср – nCV = 0, тогда (Δ S)ад = 0.
5. При изобарном процессе n = 0:  .
.
Ответ: а) 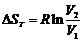 ; б) (Δ S)ад = 0; в)
; б) (Δ S)ад = 0; в)  .
.
Задача 2.14. Как изменится энтропия (Δ S) 2 г водорода, занимающего объем 40 л при температуре 270 К, если давление увеличить вдвое при постоянной температуре, а затем повысить температуру до 320 К при постоянном объеме.
| Дано: m = 2 г V = 40 л T 1 = 270 К p 2 = 2 p 1 T 2 = 320 К V = const | СИ 2∙10-3 кг 40 м3
|
| Δ S =? |
Решение.
1. Изменение энтропии определяется формулой
 ,
,
где dQ – количество теплоты, полученное в данном процессе.
2. Изменение энтропии согласно условию происходит за счет двух процессов: изотермического и изохорического. Тогда
 . (1)
. (1)
3. Количество теплоты dQ 1 и dQ 2найдем из первого начала термодинамики для этих процессов:
 .
.
4. Для изотермического процесса
 . (2)
. (2)
5. Давление р найдем из уравнения Менделеева–Клапейрона  , откуда
, откуда
 . (3)
. (3)
6. Подставим (3) в (2) и получим
 (4)
(4)
(так как dT = 0 для T = const).
7. В результате изменение энтропии составит
 ,
,
так как при T = const, р 1 V 1 = р 2 V 2.
8. Для изохорического процесса имеем:
 ,
,  ,
,
так как dV = 0и dA = 0при V = const. Тогда
 . (5)
. (5)
9. Подставив (5) и (4) в (1), получим
 =
=
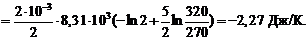
Ответ: D S = – 2, 27 Дж/К.
Задача 2.15. Паровая машина мощностью N = 14,7 кВт потребляет за время t = 1 ч работы массу m = 8,1 кг угля с удельной теплотой сгорания q = 3,3·107 Дж/кг. Температура котла Т 1 = 200 °С, температура холодильника Т 2= 58 °С. Найти фактический КПД машины и сравнить его с КПД идеальной тепловой машины, работающей по циклу Карно между теми же температурами.
| Дано: N = 14,7 кВт Т 1 = 200 °С t 2= 58 °С t = 1 ч m = 8,1 кг q = 3,3·107 Дж/кг | СИ 14,7·103 Вт 473 К 331 К 3600 с
|
| η1 =? η2 =? (η2 – η1) =? |
Решение.
1. При известной мощности N за 1 час машина совершит полезную работу:
 ,
,
2. Полная работа эквивалентна количеству теплоты, потребленному от сгоревшего угля:
 .
.
3. КПД реальной паровой машины вычислим по формуле
 . (1)
. (1)
4. КПД идеальной паровой машины:
 . (2)
. (2)
5. Подставим в (1) и (2) числовые значения:
 ,
,
 .
.
6. Вычислим разницу между КПД реальной и идеальной тепловых машин
 .
.
Ответ: 
 ,
,  .
.
Задача 2.16. Найти критическое давление и критическую температуру неона. Поправки в уравнение Ван-дер-Ваальса для неона имеют значение: а = 0,0213 Н∙м4/моль2, b = 16,97 см3/моль.
| Дано: а = 0,0213 Н∙м4/моль2 b = 16,97 см3/моль | СИ
16,97∙10-6 м3/моль |
|
| T кр =? p кр =? |
Решение. Коэффициенты a и b в уравнении состояния Ван-дер-Ваальса связаны с критическими параметрами газа соотношениями:
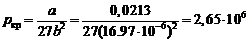 Па,
Па,
 К.
К.
Ответ: p кр(Ne) = 2,65 МПа, T кр(Ne) = 44 К.
Задача 2.17. В стеклянном капилляре вода поднимается на высоту h = 30 см. Определить диаметр капилляра. Смачивание считать полным. Коэффициент поверхностного натяжения воды равен a = 73,6×10-3 Н/м
| Дано: r = 103 кг/м3 a = 73,6×10-3 Н/м h = 30 см | СИ
0,3 м
|
| d =? |
Решение.
1.Высота подъема жидкости в капиллярной трубке
 ,
,
где J – краевой угол, R - радиус канала трубки, R = d/ 2; r – плотность жидкости; a – коэффициент поверхностного натяжения жидкости; g – ускорение свободного падения, g = 9, 8м/с2.
2. При полном смачивании стенок трубки жидкостью J = 0, соsJ = 1 и, следовательно,  откуда
откуда


3. Подставим числовые значения:

Ответ: d =100 мкм.
Задача 2.18. Определить, какую работу следует совершить, чтобы увеличить размер мыльного пузыря с d 1 = 6 мм до d 2 = 60 мм. Процесс считать изотермическим. Поверхностное натяжение мыльного раствора принять равным 40 мН/м.
| Дано: d 1 = 6 мм d 2 = 60 мм a = 40×10-3 Н/м Т = сonst | СИ 6×10-3 м 60×10-3 м
|
| A =? |
Решение.
1. Коэффициент поверхностного натяжения жидкости равен

где D E – изменение свободной поверхностной энергии пленки жидкости, связанное с изменением площади Δ S поверхности этой пленки. Откуда
D E = αD S. (1)
2. Величина D E связана с работой по выдуванию мыльного пузыря соотношением
D E = А. (2)
3. Изменение площади Δ S поверхности пленки равно
Δ S = 2 S 2 – 2 S 1 = 2(S 2 – S 1),
где S 2– площадь поверхности пузыря в конечном состоянии, S 1– площадь поверхности пузыря в исходном состоянии. Множитель два учитывает, что у мыльного пузыря две поверхности – внутренняя и внешняя.
4. Поскольку мыльный пузырь имеет сферическую поверхность, то

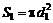 . (3)
. (3)
5. Подставим (3) и (2) в (1) и получим
 (4)
(4)
6. Подставим в (4) числовые значения:

Ответ: А = 895,28 кДж.






