Внутренняя энергия идеального газа равна
, 
или 
,
где i – число степеней свободы молекулы.
Число степеней свободы молекулы определяется как
,
где i пост – число степеней свободы поступательного движения, i пост = 3; i вращ – число степеней свободы вращательного движения; i колеб – число степеней свободы колебательного движения.
Для одноатомных молекул, рассматриваемых как материальные точки: 
.
Для двухатомных молекул, рассматриваемых как совокупность двух материальных точек, жестко связанных недеформируемой связью: 
.
Трехатомные и многоатомные нелинейные молекулы имеют шесть степеней свободы (три поступательных и три вращательных): 
.
В реальных молекулах жесткой связи между атомами не существует, поэтому учитываются также колебательные степени свободы.
Дифференциальная форма записи первого начала термодинамики
d Q =dU + δ A,
интегральная форма записи первого начала термодинамики
Q = Δ U+A,
где Q – количество теплоты, сообщенное системе; Δ U – изменение внутренней энергии системы; А – работа, совершенная системой против внешних сил.
Закон сохранения энергии в развернутом виде
и 
.
Работа расширения газа 
.
Теплоемкость
Теплоемкость C системы (тела, вещества, газа) – физическая величина, численно равная теплоте, которую необходимо сообщить системе, для того чтобы увеличить ее температуру на 1 К:
, [ С ] = Дж/К.
Удельная теплоемкость вещества c –физическая величина, численно равная теплоте, которую необходимо сообщить единице массы вещества, чтобы повысить его температуру на 1 К:
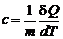, [ c ] = Дж/(кг·К).
Соотношения для расчета теплоты:
,
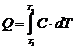в частном случае (С = const): 
;
, 
,
в частном случае (c = const):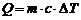 
.
Молярная теплоемкость вещества – физическая величина, численно равная теплоте, которую необходимо сообщить 1 молю вещества, для того чтобы увеличить его температуру на 1 К:
.
Размерность молярной теплоемкости [ С μ] = Дж/(моль·К).
Соотношения для расчета теплоты:
,
,
и в частном случае (С μ = const):
.
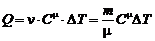Связь между различными видами теплоемкости:
.
Молярная теплоемкость идеального газа в изохорическом процессе
, 
.
где i – число степеней свободы молекулы газа; R – универсальная газовая постоянная.
Для одноатомных молекул (i = 3) 
= 1,5 R;
для двухатомных молекул (i = 5) = 2,5 R,
для многоатомных молекул (i = 6) = 3 R.
Молярная теплоемкость идеального газа в изобарическом процессе
, 
.
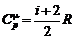Уравнение Майера: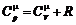 
.
Для одноатомного газа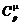 
= 2,5 R,
для двухатомного – 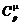= 3,5 R,
для трехатомного – 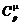= 4 R.
Отношение теплоемкостей 
.
Для газов с различным числом атомов в молекуле получаем:
γ1 = 5/3 = 1,67; γ2 = 7/5 = 1,4,
для трехатомных и многоатомных молекул γ3 = 8/6 = 1,33.
Применение первого начала термодинамики
