Зависимость массы частицы от скорости υ, сравнимой со скоростью света с (релятивистская масса):
или 
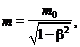
где т 0 – масса покоя частицы; υ – скорость частицы; с – скорость света в вакууме; b – скорость частицы, выраженная в долях скорости света (b = υ/с).
Релятивистское замедление хода часов:
Энергия покоя частицы: Е 0 = т 0 с 2.
Полная энергия частицы, движущейся со скоростью υ, сравнимой со скоростью света с (взаимосвязь массы и энергии релятивистской частицы):
Е = Е 0 + Т,
где Т – кинетическая энергия релятивистской частицы.
Кинетическая энергия релятивистской частицы:
.
Импульс релятивистской частицы равен
или 
Связь между полной энергией и импульсом релятивисткой частицыимеет вид
или 
.
Примеры решения задач
Задача 1.1. Мяч, брошенный с балкона вертикально вверх, через время t = 3 с упал на Землю. Определить начальную скорость мяча, если высота балкона над Землей равна 20 м. Сопротивлением воздуха пренебречь.
| Дано: t = 3 c y = 20 м | СИ |
| υ 0 =? |
Решение.
1. Движение мяча – равнопеременное, с ускорением а = g. Запишем кинематическое уравнение прямолинейного равноускоренного движениявдоль координатной оси Оу (рис. 1.1.):
. (1)
2. Решив уравнение (1) относительно υ 0, найдем
. (2)
3. Подставим числовые значения величин в (2):
.
Ответ: υ 0= 8 м/с.
Задача 1.2. Точка движется по окружности радиуса R = 20 см с постоянным тангенциальным ускорением а t = 5 см/с2. Через какое время t после начала движения нормальное ускорение аn будет равно тангенциальному?
| Дано: R = 20 см а t = 5 см/с2 а t = аn | СИ 0,2 м 5.10-2 м/ с2
|
| t =? |
Решение.
1. По условию задачи вращение является равноускоренным, поэтому справедливы следующие соотношения:
(1)
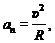(2)
где υ – линейная скорость точки.
2. Из (1) получим:
(3)
3. Из (2) выразим скорость точки:
(4)
4. Подставим (4) в (3) и учтем, что аn = а t:
(5)
5. Подставим в (5) числовые значения, выраженные в системе СИ:
Ответ: t = 2 с.
Задача 1.3. Найти угловое ускорение колеса, если известно, что через 2 с после начала равноускоренного движения вектор полного ускорения точки, лежащей на ободе, составляет угол 60о с направлением линейной скорости этой точки.
| Дано: t = 2 c α = 60о | СИ |
| ε=? |
Решение.
1. Скорость точки направлена по касательной к траектории, т. е. к окружности. По касательной направлено и тангенциальное ускорение. Значит, угол между полным ускорением и тангенциальным ускорением равен углу между ускорением и скоростью. На чертеже видно (рис.1.2), что
| an = a τ tg α. (1) 2. Выражаем an и aτ через угловые параметры движения: an = ω2 R, a τ = ε R, и подставляем в (1) ω2 R = ε R tgα. (2) 3. При нулевой начальной скорости ω = ε t. (3) | 
Рис.1.2
|
4. Подставляем (3) в (2):
ε2 t 2 = εtgα, (4)
5. Подставим числовые значения величин в (4)
ε = 
= 0,43 с-2.
Ответ: ε = 0,43 с-2.
Задача 1.4. Груз массой m = 45 кг вращается на канате длиной l = 5,0 м в горизонтальной плоскости, совершая n = 16,0 об/мин. Какой угол a с вертикалью образует канат и какова сила его натяжения Т?
| Дано: m = 45 кг l = 5,0 м n = 16,0 об/мин | СИ
0,27 об/с |
| a, Т =? |
Решение.
1. На груз действуют сила тяжести mg и сила натяжения Т каната (рис. 1.3). По второму закону Ньютона:
mg + T = ma. (1)
2. Так как движение по окружности происходит с постоянной по модулю скоростью, то полное ускорение тела в данной задаче – это нормальное ускорение, направленное к центру окружности радиуса R:
(2)
|
Рис. 1.3 |
где n – частота вращения груза.
3. Введем систему координат таким образом, чтобы ось Ох была направлена в сторону направления нормального ускорения. Запишем уравнение (1) в проекциях на оси Ох и Оу:
(3)
(4)
4. Из рис. 1.3 видно, что
R = l sina . (5)
5. Решив совместно уравнения (3) и (4) с учетом (5), имеем
(6)
(7)
6. Подставим в (6), (7) числовые значения величин в единицах СИ:
T = 45∙4∙3,142∙0,2672∙5 = 0,63 кН,
.
Ответ: Т = 0,63 кН, a = 45°.
Задача 1.5. По наклонной плоскости, составляющей с горизонтом угол 30°, движется тело массой 5 кг. К этому телу с помощью нерастяжимой нити, перекинутой через блок, привязано тело такой же массы, движущееся вертикально вниз (рис. 1.4). Коэффициент скольжения между телом и наклонной плоскостью 0,05. Определить ускорение тел и силу натяжения нити.
| Дано: m 1 = m 2 = 5кг α = 30° µ = 0,05 | СИ
|
| a =? F н =? |
Рис. 1.4
Решение.
1. Покажем на рисунке силы, действующие на каждое тело (рис. 1.4). Запишем для каждого из тел уравнение движения (второй закон Ньютона):
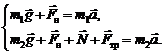
2. В проекциях на выбранные оси координат:
m 1 g – F н = m 1 a (на ось Z),
–F н + m 2 g sinα + F тр = –m 2 a (на ось X),
N – m 2 g cosα = 0 (на ось Y).
3. Учитывая, что F тр = µ N, где N = m 2 g cosα, получим систему уравнений
(1)
4. Вычтем из первого уравнения системы (1) второе:
m 1 g – m 2 g sinα – µ m 2 g cosα = m 1 a + m 2 a. (2)
5. Выразим из (2) искомое ускорение:
. (3)
6. Подставим в (3) числовые значения:
.
7. Силу натяжения найдем из первого уравнения системы (2):
F н = m 1 g – m 1 a =
= 5·9,8 – 5·2,28 = 38,6 Н.
Ответ: а = 2,28 м/с2, F н = 38,6 Н.
Задача 1.6. Молот массой m = 6 кг, двигаясь со скоростью υ = = 5 м/с, ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием равна М = 120 кг. Считая удар абсолютно неупругим, определить энергию, расходуемую на ковку (деформацию) изделия. Чему равен КПД процесса ковки при данных условиях?
| Дано: m = 6 кг υ = 5 м/с М = 120 кг | СИ |
| h =? |
Решение.
1. Примем, что система молот – изделие – наковальня является замкнутой, поскольку силы ударного взаимодействия тел гораздо больше внешних сил (силы тяжести (М+m) g и силы давления N опоры).
2. Запишем закон сохранения энергии для рассматриваемой системы:
, (1)
где W деф– энергия деформации;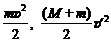 
– значения механической энергии системы до и после удара; υ' – общая скорость всех тел системы после неупругого удара.
3. Запишем закон сохранения импульса:
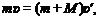(2)
откуда
(3)
4. Подставив в формулу (1) значение υ' из уравнения (3), получим
= 
.
5. Так как энергия, расходуемая на ковку изделия, является полезной, то КПД процесса ковки составляет:
Ответ: W деф = 71,4 Дж, h = 95,2 %.
Задача 1.7. Вагон массой 20 т, двигавшийся равномерно, под действием силы трения в 6 кН через некоторое время остановился. Начальная скорость вагона равна 54 км/ч. Найти: 1) работу сил трения; 2) расстояние, которое вагон пройдёт до остановки.
| Дано: m = 20 т F тр = 6 кН v 0 = 54 км/ч | СИ 2∙104 кг 6∙103 Н 15 м/с
|
| Атр =? S =? |
Решение:
1. Работа равна приращению кинетической энергии тела:
A тр = 0 – 
(1)
2. Знак минус означает, что работа сил трения отрицательна, так как силы трения направлены против движения.
3. С другой стороны, работу силы трения можно рассчитать через произведение силы на путь:
A тр = F тр s, (2)
отсюда
. (3)
4. Подставив в (2) и (3) числовые значения, получим:
A тр = 
= 2,25.106 Дж = 2,25 МДж,
s = 
= 358 м.
Ответ: Aтр = 2,25 МДж, s = 358 м.
Задача 1.8. От груза массой М, висящего на пружине жесткостью k, отрывается часть массой m. На какую высоту поднимется после этого оставшаяся часть груза?
| Дано: М k m | СИ |
| h =? |
Решение.
1. После отрыва массы m оставшаяся часть груза (M – m) движется в поле двух консервативных сил: силы упругости и силы тяжести. Полная механическая энергия системы сохраняется в процессе движения.
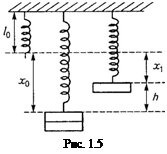
Запишем закон сохранения энергии для оставшейся массы груза. За нулевой уровень потенциальной энергии в поле тяжести примем точку подвеса пружины, а энергию упругих деформаций будем считать равной нулю для недеформированной пружины.
Введем следующие обозначения (рис. 1.5): l 0 – длина пружины в нерастянутом состоянии, х 0 –деформация пружины в начальный момент, х 1 – в момент наивысшего подъема.
2. Будем считать, что кинетическая энергия при отрыве равна нулю. В момент наивысшего подъема оставшегося груза его кинетическая энергия также равна нулю. Поскольку полная механическая энергия неизменна, можно приравнять потенциальные энергии груза (M – m) в момент отрыва части m и в момент наивысшего подъема
. (1)
3.Преобразуем формулу (1), раскрыв скобки
сократив подобные слагаемые (-(М- m) gl 0) и умножив все слагаемые на два, получим:
(2)
откуда
(3)
4. Поделим обе части уравнения (3) на (х1-х0), получим
(4)
5. Из (4) находим:
(5)
6. Начальную деформацию определяем из условия равновесия груза для М:
Mg = kx 0 или x 0 = Mg/k. (6)
7. Из рисунка 1.5 следует, что высота поднятия груза над первоначальным уровнем равна h = x 0 - x 1, тогда с учетом (5) и (6) получим
Ответ: 
.
Задача 1.9. Сплошной цилиндр массой 0,5 кг и радиусом 0,02 м вращается относительно оси, совпадающей с осью цилиндра, по закону 
. На цилиндр действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.
Дано:
m = 0,5 кг
r = 0,02 м
| СИ |
| М =? F =? |
Решение.
1. Цилиндр вращается относительно оси, совпадающей с его осью, по закону . Угловое ускорение определяется как вторая производная от угла поворота по времени:
или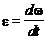 
,
где ω – угловая скорость, равная первой производной от угла по времени: 
, т.е. 
, тогда 
рад/с2.
2. Момент силы относительно оси вращения 
, так как сила действует касательно к поверхности, то 
, тогда M = Fr и
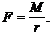(1)
3. Тормозящий момент можно определить из основного уравнения динамики вращательного движения:
М = J ε, (2)
где J – момент инерции цилиндра относительно оси вращения; так как ось вращения совпадает с осью цилиндра, то момент инерции его равен:
(3)
4. Подставляя (3) в (2), имеем
.
5. Подставим в (1) полученное числовое значение:
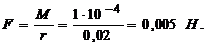
Ответ: М = 10-4 Н×м, F = 0,005 Н.
Задача 1.10. На горизонтальную ось насажен шкив радиуса R = = 30 см. На шкив намотан шнур, к свободному концу которого подвесили гирю массой m = 1,5 кг (рис. 1.6). Считая массу шкива М = 5 кг равномерно распределенной по ободу, определить ускорение а, с которым будет опускаться гиря, силу натяжения Т нити и силу давления N шкива на ось.
| Дано: R = 30 см m = 1,5 кг М = 5 кг | СИ 0,3 м |
| a =? T =? N =? |
|
Рис. 1.6 |
Решение.
1. Поскольку ускорение центра инерции шкива равно нулю, и шкив только вращается, то второй закон Ньютона для движения центра инерции твердого тела примет вид
(1)
2. Основное уравнение динамики вращательного движения твердого тела:
(2)
3. На шкив действуют силы тяжести Mg, натяжения Т нити и реакции N оси (см. рис. 1.6). Так как все три вектора параллельны одной и той же прямой, уравнение (1) можно записать в скалярном виде:
Mg + Т – N = 0. (3)
4. Шкив вращается под действием лишь момента силы Т. Следовательно, уравнение (2) преобразуется к виду
(4)
5. Момент инерции шкива, поскольку его масса распределена по ободу, найдем по формуле:
(5)
6. Уравнения (3) и (4), описывающие движение шкива, содержат три неизвестных: Т, N и e. Недостающее уравнение запишем, применив второй закон Ньютона для поступательного движения гири:
mg – T = ma. (6)
7. Поскольку шнур сматывается со шкива без проскальзывания, ускорение гири равно линейному ускорению точек на ободе шкива.
Следовательно:
(7)
8. Подставив в (4) выражения (5) и (7), получим следующую систему уравнений:
(8)
9. Выразим из системы (8) все три неизвестные величины:
, (9)
(10)
(11)
10. Подставим в уравнения (9)–(11) числовые значения:
Ответ: а = 2,3 м/с2, Т = 11,3 Н, N = 60, 3 Н.
Задача 1.11. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость ω зависит от угла поворота φ по закону ω = ω0 – b φ, где ω0и b – положительные постоянные. В момент времени t = 0 угол поворота φ = 0. Найти зависимость от времени: угла поворота и угловой скорости.
| Дано: ω = ω0 – b φ φ = 0 при t = 0 | СИ |
| φ(t) =? ω(t) =? |
Решение.
1. Угол поворота вращающегося твердого тела за время t:
(1)
где ω(t) – зависимость от времени угловой скорости.
2. Для нахождения ω(t) воспользуемся зависимостью ω(φ)
ω = ω0 – b φ . (2)
3. Продифференцируем (2) по времени t
(3)
получим дифференциальное уравнение вида
. (4)
4. Решим уравнение (4) разделив переменные
. (5)
5. Интегрируя обе части уравнения (5), найдем его решение в виде
lnω = –bt + C 1.
6. Обозначим C 1 = ln C, lnω – ln C = –bt; lnω /C = –bt и получим ω = Ce-bt.
7. Постоянную интегрирования C найдем из начального условия. Так как при t = 0 φ = 0, то ω = ω0, откуда
ω(t) = ω0 e-bt.
8. Поскольку по определению ω = d φ /dt, тоω dt = d φ, интегрируя это выражение получим
.
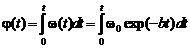9. Окончательно, зависимость угла поворота от времени имеет вид
.
Ответ: 
ω(t) = ω0 e-bt.
Задача 1.12. Круглая платформа радиуса R = 1 м, момент инерции которой J = 150 кг×м2, вращается по инерции вокруг вертикальной оси, делая n 1 = 1,5 об/с. На краю платформы стоит человек, масса которого m = 50 кг. Сколько оборотов в секунду n 2 будет совершать платформа, если человек перейдет в ее центр? Момент инерции человека рассчитывать, как для материальной точки.
| Дано: R = 1 м J = 150 кг×м2 m = 50 кг | СИ |
| n 2 =? |
Решение.
1. Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы платформа–человек выполняется закон сохранения момента импульса:
L 1 = L 2.
где L 1– начальный момент импульса системы (человек стоит на краю платформы), L 2– конечный момент импульса системы (человек стоит в центре платформы).
2. Начальный момент импульса системы равен:
L 1 = J 1w1 = (J + mR 2)2p n 1, (1)
где mR 2– момент инерции человека; 
– начальный момент инерции системы, w1 – ее начальная угловая скорость.
3. Конечный момент импульса системы равен:
L 2 = J 2w2 =2 J p n 2, (2)
где J 2 и w2– конечные момент инерции и угловая скорость системы.
4. Приравняем правые части уравнений (1) и (2):
,
откуда
(3)
5. Подставив в (3) числовые значения заданных величин и выполнив вычисление, находим
Ответ: n 2 = 2,0 об/с.
Задача 1.13. Человек массы m 2 = 60 кг стоит на краю неподвижной платформы массой m 1 =100 кг и радиусом R = 1,5 м. Платформа может вращаться без трения вокруг вертикальной оси, проходящей через ее центр. С какой угловой скоростью будет вращаться платформа, если человек будет идти по краю платформы со скоростью 1 м/с относительно платформы?
| Дано: m 1 =100 кг m 2 =60 кг R = 1,5 м υ 0= 1 м/c | СИ |
| w =? |
Решение.
1. Поскольку момент внешних сил (действующих на платформу со стороны оси) относительно платформы (назовем ее осью z) равен нулю, момент импульса системы относительно оси вращения сохраняется равным нулю при любых перемещениях человека относительно платформы, т.е.
.
2. При движении человека по краю платформы его момент импульса относительно оси z:
,
где υ 0 – скорость человека относительно неподвижной системы отсчета.
3. Поскольку платформа при этом вращается в противоположную сторону с угловой скоростью w, скорость человека относительно Земли:
.
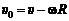4. Момент импульса вращающейся платформы имеет противоположный знак и равен:
.
5.Таким образом,
.
6. Отсюда находим
.
Ответ: 
= 0,36 рад/с.
Задача 1.14. Ракета, летевшая над поверхностью Земли на высоте h, в результате кратковременного действия мощной тормозной установки останавливается. С какой скоростью упадет ракета на Землю? Сопротивлением воздуха пренебречь.
| Дано: h | СИ |
| υ =? |
Решение.
1. Из закона сохранения энергии, примененного к системе ракета–Земля, следует, что падающая ракета будет приобретать кинетическую энергию за счет убыли потенциальной энергии в поле тяготения Земли:
Рис. 1.7
| Т = – П, (1)
где Т  – кинетическая энергия ракеты у поверхности Земли; D П = П 2 – П 1 – изменение потенциальной энергии ракеты за время ее падения из точки 1 в точку 2 (рис. 1.7).
|
2. Потенциальные энергии тяготения в начальном П1 и конечном П2 положениях ракеты определим по формулам:
(2)
(3)
где m – масса ракеты; M – масса Земли; R – радиус Земли
3. Подставим (2), (3) в (1), получим:
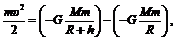(4)
4. Выразим из (4) искомую скорость:
Ответ: 
Задача 1.15. Напряженность гравитационного поля планеты на ее поверхности равна g. Определить потенциал гравитационного поля в точке, удаленной от поверхности на расстояние, равное радиусу R.
| Дано: g R | СИ |
| φ A =? |
Решение.
1. На тело массы m на поверхности планеты массы M радиуса R действует сила
.
2. Сила и потенциальная энергия связаны соотношением
F = - grad U = - dU / dr.
3. Выразим из этой формулы потенциальную энергию:
.
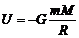4. Напряженность гравитационного поля на поверхности планеты 
; следовательно:
, g 0 = – grad φ.
5. Потенциал поля 
. Если точка А удалена на расстояние 2 R от центра планеты, то потенциал в этой точке равен
.
6.Так как g 0 R = GM, окончательно получим 
.
Ответ: .
Задача 1.16. Определить импульс и кинетическую энергию электрона, движущегося со скоростью 0,7 с (где с – скорость света в вакууме).
| Дано: υ = 0,7 c | СИ |
| p =? T =? |
Решение.
1. Импульсом частицы называется произведение массы частицы на скорость ее движения:
р = тυ. (1)
2. Так как скорость электрона близка к скорости света, то не обходимо учесть зависимость массы от скорости, определяемую по формуле
, (2)
где m – масса движущейся частицы, m 0 – масса покоящейся частицы.
3. Подставив (2) в (1), получим
. (3)
4. Поскольку b = υ/с = 0,7, получим
5. Кинетическая энергия T в релятивистской механике определяется как разность между полной энергией частицы Е = тс 2 и ее энергией покоя Е 0 = т 0 с 2, т.е. с учетом (2)
. (4)
6. Найдем численное значение T, подставив числовые данные в формулу (4):
Ответ: р = 2,7×10-22 кг×м/с, Т = 3,3×10-14Дж.
Задача 1.17. Собственное время жизни некоторой нестабильной частицы Δ t 0 = 10 нс. Какой путь пролетит эта частица до распада в лабораторной системе отсчета, в которой ее время жизни Δ t = = 20 нс?
| Дано: Δ t 0 = 10 нс Δ t = 20 нс | СИ |
| l =? |
Решение.
1. Соотношение между указанными временами 
тогда 
2. Возведем обе части последнего уравнения в квадрат и получим 
3. Путь в лабораторной системе отсчета
Ответ: l = 5,16 м.
