Но:
§ если расходимость ряда 
установлена в результате применения признака Даламбера ( теорема 1.7 на стр. 31) или признака Коши ( теорема 1.8 на стр. 36),
т.е. если получили
или 
,
то в этом случае
оба ряда и 
расходятся.
Ä Замечание 3 (Сходимость ряда с комплексными членами)
Ряд вида
(где 
действительные числа,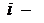 
мнимая единица)
сходится тогда и только тогда, когда сходятся два ряда — 
и 
.
Функциональные ряды
10. Определения
1) Функциональным рядом называется ряд вида
,
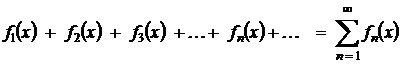члены которого 
— функции от 
.
2) Совокупность значений , при которых функции определены и функциональный ряд 
сходится, называют областью сходимости 
функционального ряда.
3) Если обозначить:
(
— сумма ряда),
(
— 
частичная сумма ряда),
(
— остаток (
остаток) ряда),
то сумму 
ряда можно представить в виде
.
4) Функциональный ряд называется равномерно сходящимся в некоторой области сходимости , если:
для любого сколь угодно малого 
найдется такой номер 
, что при всех 
выполняется неравенство
.
11. Теорема (Признак Вейерштрасса равномерной сходимости функционального ряда)
Функциональный ряд
сходится равномерно (и абсолютно) в некоторой области сходимости , если существует сходящийся числовой ряд с положительными членами
такой, что:
для всех значений 
выполняются неравенства
12. Теорема (Интегрирование функциональных рядов)
Если функциональный ряд
(где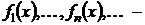 
непрерывные функции)
равномерно сходится в некоторой области и имеет сумму 
,
То
ряд
(где промежуток 
)
сходится и имеет сумму 
:
.
Ä Замечание (Интегрирование степенных рядов)
Степенной ряд вида 
(или 
) можно интегрировать на любом промежутке, лежащем внутри интервала сходимости.
Ä
13. Теорема (Дифференцирование функциональных рядов)
Если выполняются два условия:
1) функциональный ряд
(где функции 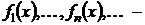определены в некоторой области 
и имеют в этой области производные 
)
сходится в области и имеет сумму ;
2) ряд, составленный из производных
,
сходится равномерно в той же области ,
то
сумма ряда производных 
равна производной 
от суммы первоначального ряда:
.
Ä Замечание (Дифференцирование степенных рядов)
Степенной ряд вида (или ) можно почленно дифференцировать внутри его интервала сходимости.
Ä
Степенные ряды
14. Определения
Степенным рядом называется функциональный ряд вида
или
.
15. Теорема (Абеля)
1. Если степенной ряд 
сходится при некотором значении 
, то он сходится (и притом абсолютно) при всяком значении 
, удовлетворяющем неравенству
;
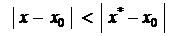2. Если степенной ряд расходится при некотором значении 
, то он расходится при всяком значении , удовлетворяющем неравенству
.
Ä Следствие
¨ Для всякого степенного ряда
существует интервал сходимости
с центром в точке 
,
внутри которого ряд сходится абсолютно и вне которого
(т.е. при 
) ряд расходится.
¨ На концах интервала сходимости (в точках 
) возможна как сходимость, так и расходимость степенного ряда.
¨ Число 
(половина длины интервала сходимости) называют радиусом сходимости степенного ряда.
В частных случаях радиус сходимости может быть равен нулю или бесконечности.
Если 
, то степенной ряд сходится только при 
; если 
, то ряд сходится на всей числовой прямой.
Ä
