1. Теорема (Необходимый признак сходимости)
Если ряд 
сходится, то общий член ряда 
стремится к нулю при 
, т.е.:
.
Таким образом,
если 
, то ряд расходится;
если же , то ряд может быть как сходящимся,
так и расходящимся.
2. Теорема (Первый признак сравнения)
Пусть и 
— ряды с положительными членами,
причем
для всех номеров 
, начиная с некоторого
номера 
.
Тогда:
1) если ряд сходится, то сходится и ряд ;
2) если ряд расходится, то расходится и ряд .
Иначе говоря,
из сходимости ряда с бóльшими членами следует сходимость ряда с мéньшими членами;
из расходимости ряда с мéньшими членами следует расходимость ряда с бóльшими членами.
3. Теорема (Второй признак сравнения (признак сравнения в предельной форме))
Пусть и — ряды с положительными членами, причем существует конечный и отличный от нуля предел
.
Тогда оба ряда и одновременно сходятся или одновременно расходятся (другими словами, имеют одинаковый характер сходимости).
4. Теорема (Признак Даламбера)
Пусть — ряд с положительными членами, и существует конечный предел
.
Тогда:
1) если 
, то данный ряд сходится;
2) если 
, то данный ряд расходится;
3) если 
, то ряд может сходиться или расходиться; в этом случае требуется дополнительное исследование ряда с помощью других методов.
Ä Замечание 1
Если 
, но, начиная с некоторого номера 
, имеет место неравенство 
, то ряд расходится.
Ä Замечание 2
Ряд будет расходящимся и в том случае, если 
.
5. Теорема (Радикальный признак Коши)
Пусть — ряд с положительными членами, и существует конечный предел
.
Тогда:
1) если , то данный ряд сходится;
2) если , то данный ряд расходится;
3) если , то ряд может сходиться или расходиться; в этом случае требуется дополнительное исследование ряда с помощью других методов.
Ä Замечание
Ряд будет расходящимся и в том случае, если 
.
Ä
6. Теорема 1.9 (Интегральный признак сходимости)
Пусть — ряд с положительными членами, и 
.
Тогда,
если соответствующая функция 
— положительная,
непрерывная и монотонно убывающая на промежутке
, то:
ряд и несобственный интеграл 
сходятся или
расходятся одновременно.
Знакопеременные ряды
7. Определения
1) Знакочередующимся называется ряд, в котором любые два соседних члена имеют разные знаки, т.е. ряд вида
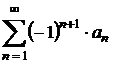или 
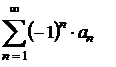, где 
.
2) Знакопеременным называется ряд, содержащий и положительные, иотрицательные члены (расположенные в произвольном порядке).
8. Теорема (Признак Лейбница сходимости знакочередующегося ряда)
Знакочередующийся ряд сходится, если выполняются два условия:
1) абсолютные величины членов ряда монотонно убывают, т.е.
;
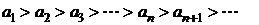2) общий член ряда стремится к нулю при 
, т.е.
.
9. Теорема (Сходимость знакопеременного ряда)
Пусть дан знакопеременный ряд 
, где 
произвольные числа (действительные или комплексные).
Если сходится ряд 
(составленный из абсолютных величин исходного ряда), то исходный ряд также сходится. В этом случае ряд называется абсолютно сходящимся.
Если же знакопеременный ряд сходится, а ряд расходится, то ряд называется условно сходящимся.
Ä Замечание 1
Для исследования абсолютной сходимости ряда к ряду можно применять все признаки, используемые при исследовании рядов с положительными членами.
Ä Замечание 2
