
Задача 12. Найти область сходимости ряда.
(См.:
§ п. I.1.4. Функциональные ряды. Равномерная сходимость. Признак
Вейерштрасса равномерной сходимости ряда. Интегрирование и дифференцирование равномерно сходящихся рядов)
12.1  . .
| 12.2  . .
|
12.3  . .
| 12.4  . .
|
12.5  . .
| 12.6  . .
|
12.7  . .
| 12.8  . .
|
12.9  . .
| 12.10  . .
|
12.11  . .
| 12.12  . .
|
8.13  . .
| 12.14  . .
|
12.15  . .
| 12.16  . .
|
12.17  . .
| 12.18 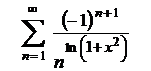 . .
|
12.19  . .
| 12.20  . .
|
12.21 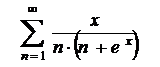 . .
| 12.22  . .
|
12.23  . .
| 12.24 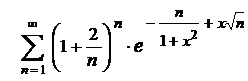 . .
|
12.25  . .
| 12.26  . .
|
12.27  . .
| 12.28  . .
|
12.29  . .
| 12.30 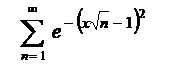 . .
|
12.31  . .
|
Указание к выполнению
Использовать алгоритм нахождения области сходимости функционального ряда на стр. 62.
Пример выполнения задания.
См. пример I.1. - 8 (Определение области сходимости функционального ряда) на стр. 63.
Задача 13. Найти область сходимости ряда.
(См.:
§ п. I.1.4. Функциональные ряды. Равномерная сходимость. Признак
Вейерштрасса равномерной сходимости ряда. Интегрирование и дифференцирование равномерно сходящихся рядов).
13.1  . .
| 13.2  . .
|
13.3  . .
| 13.4 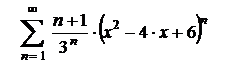 . .
|
13.5  . .
| 13.6  . .
|
13.7  . .
| 13.8  . .
|
13.9  . .
| 13.10  . .
|
13.11  . .
| 13.12  . .
|
13.13  . .
| 13.14  . .
|
13.15  . .
| 13.16  . .
|
13.17  . .
| 13.18  . .
|
13.19  . .
| 13.20  . .
|
13.21  . .
| 13.22  . .
|
13.23  . .
| 13.24  . .
|
13.25  . .
| 13.26  . .
|
13.27 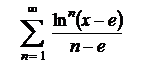 . .
| 13.28  . .
|
13.29  . .
| 13.30  . .
|
13.31  . .
|
Указание к выполнению
Использовать алгоритм нахождения области сходимости функционального ряда на стр. 62.
Пример выполнения задания.
См. пример I.1. - 8 (Определение области сходимости функционального ряда) на стр. 63.
Задача 14. Найти сумму ряда.
(См.:
§ п. I.1.4. Функциональные ряды. Равномерная сходимость. Признак
Вейерштрасса равномерной сходимости ряда. Интегрирование и дифференцирование равномерно сходящихся рядов).
14.1  . .
| 14.2  . .
|
14.3 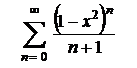 . .
| 14.4  . .
|
14.5  . .
| 14.6  . .
|
14.7  . .
| 14.8  . .
|
14.9  . .
| 14.10  . .
|
14.11  . .
| 14.12  . .
|
14.13  . .
| 14.14  . .
|
14.15  . .
| 14.16  . .
|
14.17  . .
| 14.18  . .
|
14.19  . .
| 14.20  . .
|
14.21  . .
| 14.22 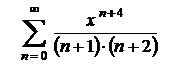 . .
|
14.23  . .
| 14.24  . .
|
14.25  . .
| 14.26  . .
|
14.27  . .
| 14.28 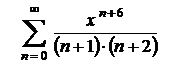 . .
|
14.29  . .
| 14.30  . .
|
14.31  . .
|
Указание к выполнению
Использовать почленное интегрирование функционального ряда ( теорема 1.13 (Интегрирование функциональных рядов) на стр. 77).
Пример выполнения задания.
См. пример I.1. - 9 (Вычисление суммы ряда почленным интегрированием) на стр. 78.
Задача 15. Найти сумму ряда.
(См.:
§ п. I.1.4. Функциональные ряды. Равномерная сходимость. Признак
Вейерштрасса равномерной сходимости ряда. Интегрирование и дифференцирование равномерно сходящихся рядов).
15.1  . .
| 15.2  . .
|
15.3  . .
| 15.4  . .
|
15.5  . .
| 15.6  . .
|
15.7  . .
| 15.8  . .
|
15.9  . .
| 15.10  . .
|
15.11  . .
| 15.12  . .
|
15.13  . .
| 15.14 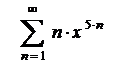 . .
|
15.15  . .
| 15.16  . .
|
15.17 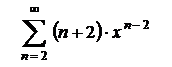 . .
| 15.18  . .
|
15.19  . .
| 15.20  . .
|
15.21  . .
| 15.22  . .
|
15.23  . .
| 15.24  . .
|
15.25  . .
| 15.26  . .
|
15.27  . .
| 15.28  . .
|
15.29  . .
| 15.30  . .
|
15.31  . .
|
Указание к выполнению
Использовать почленное дифференцирование функционального ряда ( теорема 1.14 (Дифференцирование функциональных рядов) на стр. 87).
Пример выполнения задания.
См. пример I.1. - 10 (Вычисление суммы ряда почленным дифференцированием) на стр. 88.
Задача 16.
Разложить в ряд Фурье функцию  с периодом
с периодом  ;
;
при этом,
если функция задана на полупериоде (т.е. на промежутке, длина которого равна половине периода  ), то разложить в ряд Фурье по синусам или по косинусам.
), то разложить в ряд Фурье по синусам или по косинусам.
(См.:
§ п. I.1.8. Тригонометрические ряды. Ряд Фурье, сходимость рядов Фурье, коэффициенты Фурье. Ряд Фурье для четных и нечетных функций;
§ п. I.1.9. Ряд Фурье для функций с «двойной симметрией»;
§ п. I.1.10. Ряд Фурье для функций, заданных на полупериоде. Разложение в ряд Фурье непериодических функций).
16.1

| 16.2
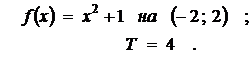
|
16.3

| 16.4

|
16.5

| 16.6

|
16.7

| 16.8

|
16.9

| 16.10

|
16.11

| 16.12

|
16.13

| 16.14

|
16.15

| 16.16

|
16.17

| 16.18

|
16.19

| 16.20

|
16.21

| 16.22

|
16.23

| 16.24

|
16.25

| 16.26

|
16.27

| 16.28

|
16.29
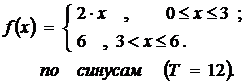
| 16.30
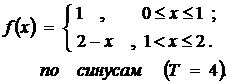
|
16.31

|
Указание к выполнению
Использовать формулы разложений в ряд Фурье:
§ периодических функций с произвольным периодом  ;
;
§ с периодом  ;
;
§ четных и нечетных функций;
§ функций, заданных на полупериоде,
из п. I.1.8. – I.1.10 ( или из приложения 3, стр. 306 – 312).
Пример выполнения задания.
См.:
§ пример I.1. – 18 (Разложение функций с периодом  в ряд Фурье) на стр. 155;
в ряд Фурье) на стр. 155;
§ пример I.1. – 19 (Разложение функций с произвольным периодом  в ряд Фурье) на стр. 174;
в ряд Фурье) на стр. 174;
§ пример I.1. – 21 (Разложение в ряд Фурье функций, заданных на полупериоде) на стр. 196.
ПРИЛОЖЕНИЯ
Приложение 1
|

Приложение 2
|
Приложение 3
Основные теоремы и формулы теории рядов





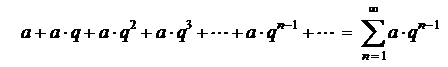 ,
,  составленный из членов бесконечной геометрической прогрессии со
знаменателем
составленный из членов бесконечной геометрической прогрессии со
знаменателем  и первым членом
и первым членом  , называется
геометрическим рядом.
Если
, называется
геометрическим рядом.
Если 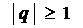 , то геометрический ряд (1) расходится;
если
, то геометрический ряд (1) расходится;
если  , то ряд (1) сходится, и его сумма
, то ряд (1) сходится, и его сумма  определяется формулой
определяется формулой  .
Замечание
1. Вычислить сумму ряда (1), начиная с
.
Замечание
1. Вычислить сумму ряда (1), начиная с  слагаемого
слагаемого
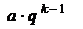 , можно по формуле
, можно по формуле  .
2. Сумму
.
2. Сумму  первых слагаемых ряда (1) можно вычислить
по формуле
первых слагаемых ряда (1) можно вычислить
по формуле 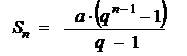 .
¨ Ряд
.
¨ Ряд

 называется гармоническим. Гармонический ряд расходится.
¨ Ряд
называется гармоническим. Гармонический ряд расходится.
¨ Ряд
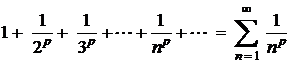
 называется рядом Дирихле (обобщенным гармоническим рядом).
Ряд Дирихле сходится при
называется рядом Дирихле (обобщенным гармоническим рядом).
Ряд Дирихле сходится при  и расходится при
и расходится при  .
Гармонический ряд является частным случаем ряда Дирихле при
.
Гармонический ряд является частным случаем ряда Дирихле при  .
.
 некоторых элементарных функций
1.
некоторых элементарных функций
1.  2.
2.  3.
3. 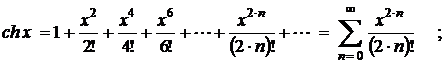 4.
4. 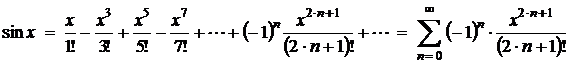 ;
5.
;
5.  ;
Разложения (1) – (5) справедливы для всех
;
Разложения (1) – (5) справедливы для всех  .
6.
.
6.  ;
;
 7.
7.  ;
;
 8.
8. 



