Исследуем сходимость степенного ряда в граничных точках интервала сходимости.
§ При 
:
.
Ряд 
расходится, так как не выполняется необходимый признак сходимости ряда: 
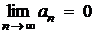(в нашем случае 
).
Таким образом,
при степенной ряд расходится.
§ При 
:
.
Ряд 
расходится.
Таким образом,
при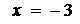 
степенной ряд расходится.
3. Объединяя результаты п. 1 и 2 решения, окончательно получаем:
степенной ряд 
сходится при 
.
D
Задача 9. Разложить функцию 
в ряд Тейлора по степеням 
.
(См.:
§ п. I.1.6. Ряды Тейлора и Маклорена. Разложение в степенные ряды некоторых элементарных функций).
9.1  .
| 9.2  .
|
9.3  .
| 9.4  .
|
9.5  .
| 9.6  .
|
9.7  .
| 9.8  .
|
9.9  .
| 9.10  .
|
9.11  .
| 9.12  .
|
9.13  .
| 9.14  .
|
9.15  .
| 9.16  .
|
9.17  .
| 9.18  .
|
9.19  .
| 9.20  .
|
9.21  .
| 9.22  .
|
9.23  .
| 9.24  .
|
9.25  .
| 9.26  .
|
9.27  .
| 9.28  .
|
9.29  .
| 9.30  .
|
9.31  .
|
Указание к выполнению
1. Преобразовать функцию к виду, допускающему использование табличных разложений функций 
.
(См. табл. 2 на стр. 122 или приложение 2).
2. Найти разложение функции в ряд Тейлора, используя:
§ табличные разложения;
§ сложение (вычитание) рядов;
§ умножение ряда на число.
(См. также на стр. 123 – 124 приемы, применяемые при разложении в степенные ряды).
3. Определить область сходимости полученного рядак функции .
Ñ Пример выполнения задания.
(См. также:
§ пример I.1. - 13 (Разложение функций в степенные ряды) на стр. 124) )
Разложить функцию 
в ряд Тейлора по степеням 
.
Решение
1. Преобразуем функцию к виду, допускающему использование табличного разложения
, 
. 
Имеем:
.
Таким образом, получили:
. 
2. Теперь разложим в ряд Тейлора по степеням каждую из полученных функций: 
и 
.
Имеем:
§ разложениефункции является табличным разложением (1) с областью сходимости (2):
,
.
§ получим разложение функции по степеням :
,
или
. 
3. Подставляя полученные разложения (2) и (4) в равенство (3), получаем искомое разложение функции :
,
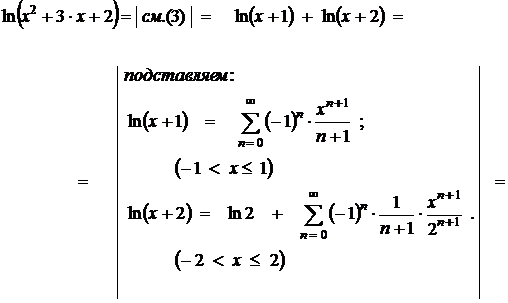
или
. 
— искомое разложение.
Область сходимости ряда (6): 
.
Итак, получили:
Разложение функции в ряд Тейлора
По степеням имеет вид
.
D
Задача 10. Вычислить интеграл с точностью до 
.
(См.:
§ п. I.1.7. Приложения степенных рядов: вычисление значений функций с помощью рядов; вычисление определенных интегралов с помощью рядов; вычисление пределов с помощью рядов).
10.1  .
| 10.2  .
|
10.3  .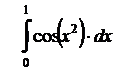
| 10.4  .
|
10.5  .
| 10.6  .
|
10.7  .
| 10.8  .
|
10.9  .
| 10.10  .
|
10.11  .
| 10.12  .
|
10.13  .
| 10.14  .
|
10.15  .
| 10.16  .
|
10.17  .
| 10.18  .
|
10.19  .
| 10.20  .
|
10.21  .
| 10.22  .
|
10.23  .
| 10.24  .
|
10.25  .
| 10.26  .
|
10.27  .
| 10.28  .
|
10.29  .
| 10.30  .
|
10.31  .
|
Указание к выполнению
1. Разложить подынтегральную функцию в степенной ряд (ряд Тейлора) по степеням :
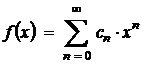
и определить его область сходимости.
(Использовать стандартные разложения из приложения 2).
2. Проинтегрировать почленно полученный ряд по заданному промежутку интегрирования, используя формулу Ньютона – Лейбница:
.
(При этом промежуток интегрирования должен лежать в области сходимости ряда).
