Для этого исследуем сходимость ряда
, 
составленного из абсолютных величин ряда (1).
Воспользуемся вторым признаком сравнения:
если
,
то оба ряда 
и 
одновременно сходятся или одновременно расходятся (другими словами, имеют одинаковый характер сходимости).
Чтобы выбрать эталонный ряд для сравнения с рядом (2), сначала оценим общий член 
ряда (2).
Имеем:
,
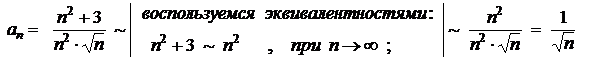или
. 
Выберем в качестве эталонного ряда гармонический ряд
. 
Найдем предел отношения общего члена 
исследуемого ряда (2) к общему члену 
эталонного ряда (4):
условие 2-го признака сравнения выполняется, и, следовательно, оба ряда (2) и (4) имеют одинаковый характер сходимости.
Ряд (4) 
расходится (так как ряд Дирихле 
при 
расходится).
Значит, расходится и ряд (2), составленный из абсолютных величин исходного знакочередующегося ряда (1) 
.
Следовательно, ряд (1) не является абсолютно сходящимся.
Исследуем условную сходимость ряда (1).
Применим признак Лейбница сходимости знакочередующегося ряда.
Согласно признаку Лейбница,
знакочередующийся ряд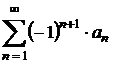 
сходится, если выполняются два условия:
а) абсолютные величины членов ряда монотонно убывают, т.е.
;
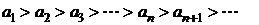б) общий член ряда стремится к нулю при 
, т.е.
.
Для ряда (1) 
:
§ условие (необходимое условие сходимости ряда) выполняется (см. п. 1 решения);
§ проверим, выполняется ли условие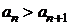 
:
так как числители у дробей остаются постоянными, а знаменатели растут с увеличением номера, то значения дробей уменьшаются, а значит, последовательность 
монотонно убывает, т.е. выполняется условие 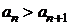признака Лейбница.
Таким образом,
Для данного знакочередующегося ряда (1) выполнены оба условия признака Лейбница, и, следовательно, этот ряд сходится.
Но, как было показано выше (п. 2 решения), данный ряд не является абсолютно сходящимся, поэтому он сходится условно.
Итак, окончательно получили:
Знакочередующийся ряд
Сходится условно.
D
Задача 8. Найти область сходимости ряда.
(См.:
§ п. I. 1. 5. Степенные ряды. Теорема Абеля. Область сходимости степенного ряда, интервал (круг) сходимости и радиус сходимости).
8.1  .
| 8.2  .
|
8.3  .
| 8.4  .
|
8.5  .
| 8.6  .
|
8.7  .
| 8.8  .
|
8.9  .
| 8.10  .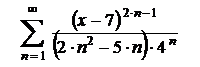
|
8.11  .
| 8.12  .
|
8.13  .
| 8.14  .
|
8.15  .
| 8.16  .
|
8.17  .
| 8.18  .
|
8.19  .
| 8.20  .
|
8.21  .
| 8.22  .
|
8.23  .
| 8.24  .
|
8.25  .
| 8.26  .
|
8.27  .
| 8.28  .
|
8.29  .
| 8.30  .
|
8.31  .
|
Указание к выполнению
(См. также: способы отыскания интервала и радиуса сходимости степенного ряда на стр. 96 – 99)
1. Для степенного ряда вида
в случае, когда все коэффициенты ряда 
(т.е. ряд содержит все целые положительные степени выражения 
), интервал сходимости определяется неравенством
где радиус сходимости 
определяется по формуле Даламбера (2) или по формуле Коши (3):
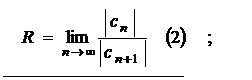
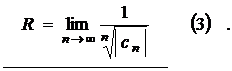
2. Если же степенной ряд содержит не все целые положительные степени выражения (например, степенной ряд содержит члены только с четными или только с нечетными степенями выражения ),
то
в этом случае степенной ряд рассматривается как функциональный ряд общего вида
,
интервал сходимости которого определяется с помощью признака Даламбера (4) или признака Коши (5) (применяемых к ряду 
):
.
3. Исследовать сходимость степенного ряда в граничных точках интервала сходимости.
Ñ Пример выполнения задания.
(См. также:
§ пример I.1. - 11 (Определение области сходимости степенного ряда) на стр. 101 ).
Найти область сходимости ряда
.
Решение
Имеем степенной ряд вида
. 
В данном случае ряд содержит не все, а только четные степени выражения 
.
Поэтому (см. указание к выполнению ) степенной ряд (1) следует рассматривать как функциональный ряд общего вида
,
и определять интервал сходимости с помощью признака Даламбера или признака Коши (применяя их к ряду ).
Воспользуемся признаком Коши:
.
Имеем:
.
Получили:
