D
Задача 6. Исследовать на сходимость ряд.
(См.:
§ п. I.1.2. Ряды с положительными членами. Достаточные признаки сходимости рядов с положительными членами: первый и второй признаки сравнения, признак Даламбера, радикальный признак Коши интегральный признак).
6.1  .
| 6.2  .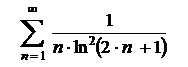
|
6.3  .
| 6.4  .
|
6.5  .
| 6.6  .
|
6.7  .
| 6.8  .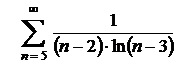
|
6.9  .
| 6.10  .
|
6.11  .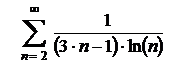
| 6.12  .
|
6.13  .
| 6.14  .
|
6.15  .
| 6.16  .
|
6.17  .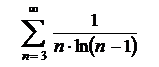
| 6.18  .
|
6.19  .
| 6.20  .
|
6.21  .
| 6.22  .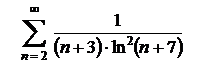
|
6.23  .
| 6.24  .
|
6.25  .
| 6.26  .
|
6.27  .
| 6.28  .
|
6.29  .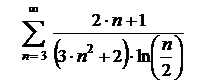
| 6.30  .
|
6.31  .
|
Указание к выполнению
Использовать интегральный признак сходимости.
1. Упростить выражение для общего члена данного ряда 
, заменив 
эквивалентным:
.
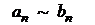2. Исследовать сходимость полученного ряда 
по интегральному признаку сходимости ( теорема 1.9 (Интегральный признак сходимости) на стр. 40).
3. Исследовать сходимость исходного ряда с помощью второго признака сравнения ( теорема 1.6 (Второй признак сравнения (признак сравнения в предельной форме)) настр. 21), используя ряд в качестве эталонного ряда.
Ñ Пример выполнения задания.
(См. также:
§ пример I.1. - 6 (Исследование рядов на сходимость с помощью интегрального признака) на стр. 41)
Исследовать на сходимость ряд
. 
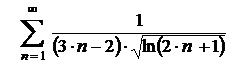Решение
Упростим выражение для общего члена ряда (1).
Имеем:
.
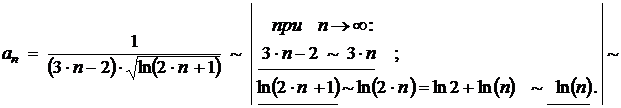
Получили:
. 
Исследуем сходимость полученного ряда
По интегральному признаку сходимости.
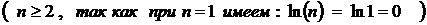
По интегральному признаку,
сходимость ряда 
(
) определяется сходимостью несобственного интеграла 
, если функция 
— положительная, непрерывная и монотонно убывающая на промежутке 
.
В нашем случае имеем:
.
Рассмотрим функцию 
.
Эта функция является положительной, непрерывной и монотонно убывающей на промежутке 
.
Следовательно, по интегральному признаку, сходимость ряда определяется сходимостью несобственного интеграла
.
Получили:
данный несобственный интеграл расходится, а значит, по интегральному признаку расходится и ряд (3)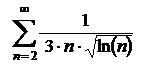 
.
Исследуем сходимость исходного ряда (1) с помощью второго признака сравнения, используя расходящийся ряд (3) в качестве эталонного ряда.
По второму признаку сравнения, найдем предел отношения общего члена 
ряда (1) к общему члену 
эталонного ряда (3):
условие 
2-го признака сравнения выполняется и, следовательно, оба ряда (1) и (3) имеют одинаковый характер сходимости.
Ряд (3) расходится (показано в п. 2 решения).
Значит, расходится и исходный ряд (1) .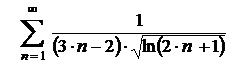
Итак, получили:
Ряд
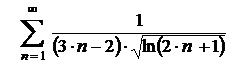
Расходится.
D
Задача 7. Исследовать на сходимость ряд.
(См.:
§ п. I. 1. 3. Знакопеременные ряды. Признак Лейбница сходимости знакочередующегося ряда. Условная и абсолютная сходимость).
7.1  .
| 7.2  .
|
7.3  .
| 7.4  .
|
7.5  .
| 7.6  .
|
7.7  .
| 7.8  .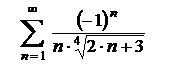
|
7.9  .
| 7.10  .
|
7.11  .
| 7.12  .
|
7.13  .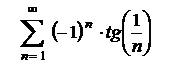
| 7.14  .
|
7.15  .
| 7.16  .
|
7.17  .
| 7.18  .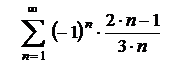
|
7.19  .
| 7.20  .
|
7.21  .
| 7.22  .
|
7.23  .
| 7.24  .
|
7.25  .
| 7.26  .
|
7.27  .
| 7.28  .
|
7.29  .
| 7.30  .
|
7.31  .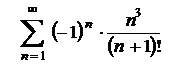
|
Указание к выполнению (см.также общий алгоритм исследования сходимости знакопеременных рядов на стр. 50)
1. Проверить необходимый признак сходимости ряда:
(если 
, то ряд расходится, так как не выполнено необходимое условие сходимости ряда).
2. Проверить абсолютную сходимость ряда.
Для этого нужно исследовать сходимость ряда, составленного из абсолютных величин исходного ряда, используя: признаки сравнения, признак Даламбера, признак Коши (радикальный), интегральный признак сходимости.
Если ряд, составленный из абсолютных величин, сходится, то исходный ряд сходится абсолютно.
3. Если исходный знакочередующийся ряд вида 
не является абсолютно сходящимся, то исследовать его условную сходимость.
Для этого использовать признак Лейбница ( теорема 1.10 на стр. 47).
Ñ Пример выполнения задания.
(См. также:
§ пример I.1. - 7 (Исследование сходимости знакопеременных рядов) на стр. 51).
Исследовать на сходимость ряд
.
Решение
Имеем знакочередующийся ряд вида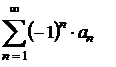 
, где 
.
1. Проверим выполнение необходимого условия сходимости ряда:
.
Имеем:
.
