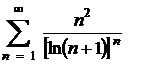D
Задача 3. Исследовать на сходимость ряд.
(См.:
§ п. I.1.2. Ряды с положительными членами. Достаточные признаки сходимости рядов с положительными членами: первый и второй признаки сравнения, признак Даламбера, радикальный признак Коши, интегральный признак).
3.1  .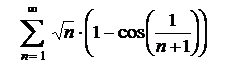
| 3.2  .
|
3.3  .
| 3.4  .
|
3.5  .
| 3.6  .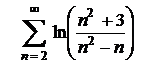
|
3.7  .
| 3.8  .
|
3.9  .
| 3.10  .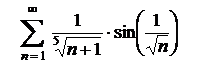
|
3.11  .
| 3.12  .
|
3.13  .
| 3.14  .
|
3.15  .
| 3.16  .
|
3.17  .
| 3.18  .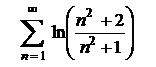
|
3.19  .
| 3.20  .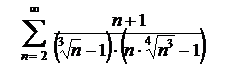
|
3.21  .
| 3.22  .
|
3.23  .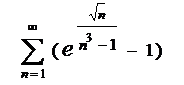
| 3.24  .
|
3.25  .
| 3.26  .
|
3.27  .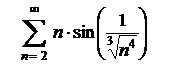
| 3.28  .
|
3.29  .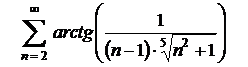
| 3.30  .
|
3.31  .
|
Указание к выполнению
Использовать:
§ второй признак сравнения ( теорема 1.6 настр. 22).
При этом в качестве эталонных рядов (для сравнения с исследуемыми рядами) использовать ряды из приложения 2.
Ñ Пример выполнения задания.
(См. также:
§ пример I.1. - 3 (Исследование рядов на сходимость с помощью второго признака сравнения) на стр. 22).
Исследовать на сходимость ряд
. 
Решение
Согласно 2-му признаку сравнения,
если
для рядов 
и 
существует конечный и отличный
от нуля предел
,
то оба ряда и одновременно сходятся или одновременно расходятся (другими словами, имеют одинаковый характер сходимости).
Для применения этого выберем так называемый эталонный ряд, сходимость (или расходимость) которого уже известна (или легко определяется).
Чтобы выбрать эталонный ряд для сравнения с рядом (1), сначала оценим общий член 
ряда (1).
Имеем:
.
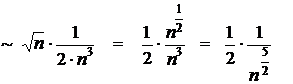Таким образом,
. 
Выберем в качестве э талонного ряда ряд
. 
Найдем предел отношения общего члена исследуемого ряда (1) к общему члену 
эталонного ряда (3):
условие 2-го признака сравнения выполняется и, следовательно, оба ряда — данный и эталонный 
— имеют одинаковый характер сходимости.
Ряд сходится (так как ряд Дирихле 
при 
сходится).
Значит, сходится и ряд .
Итак, получили:
Ряд
Сходится (по 2-му признаку сравнения).
D
Задача 4. Исследовать на сходимость ряд.
(См.:
§ п. I.1.2. Ряды с положительными членами. Достаточные признаки сходимости рядов с положительными членами: первый и второй признаки сравнения, признак Даламбера, радикальный признак Коши, интегральный признак).
4.1  .
| 4.2  .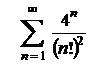
|
4.3  .
| 4.4  .
|
4.5  .
| 4.6  .
|
4.7  .
| 4.8  .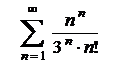
|
4.9  .
| 4.10  .
|
4.11  .
| 4.12  .
|
4.13  .
| 4.14  .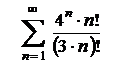
|
4.15  .
| 4.16  .
|
4.17  .
| 4.18  .
|
4.19  .
| 4.20  .
|
4.21  .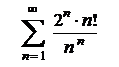
| 4.22  .
|
4.23  .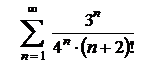
| 4.24  .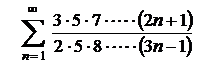
|
4.25  .
| 4.26  .
|
4.27  .
| 4.28  .
|
4.29  .
| 4.30  .
|
4.31  .
|
Указание к выполнению
Использовать признак Даламбера ( теорема 1.7 на стр. 31).
Ñ Пример выполнения задания.
(См. также:
§ пример I.1. - 4 (Исследование рядов на сходимость с помощью признака Даламбера) на стр. 32).
Исследовать на сходимость ряд
. 
Решение
По признаку Даламбера,
сходимость ряда определяется в зависимости от величины
предела отношения
.
А именно:
1) если 
, то ряд сходится;
2) если 
, то ряд расходится;
3) если 
, то в этом случае требуется дополнительное исследование ряда с помощью других методов.
Исследуем с помощью признака Даламбера ряд (1).
Найдем предел отношения 
.
Имеем:
.
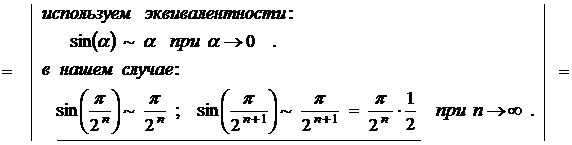
Получили:
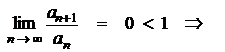
исследуемый ряд сходится по признаку Даламбера.
Итак, ряд
сходится (по признаку Даламбера).
Задача 5. Исследовать на сходимость ряд.
См.:
§ п. I.1.2. Ряды с положительными членами. Достаточные признаки сходимости рядов с положительными членами: первый и второй признаки сравнения, признак Даламбера, радикальный признак Коши, интегральный признак).
5.1  .
| 5.2  .
|
5.3  .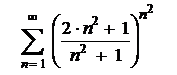
| 5.4  .
|
5.5  .
| 5.6  .
|
5.7  .
| 5.8  .
|
5.9  .
| 5.10  .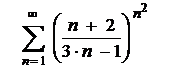
|
5.11  .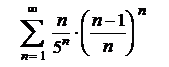
| 5.12  .
|
5.13  .
| 5.14  .
|
5.15  .
| 5.16  .
|
5.17  .
| 5.18  .
|
5.19  .
| 5.20  .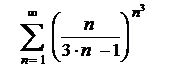
|
5.21  .
| 5.22  .
|
5.23  .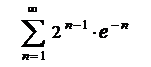
| 5.24  .
|
5.25  .
| 5.26  .
|
5.27  .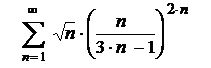
| 5.28  .
|
5.29  .
| 5.30  .
|
5.31  .
|
Указание к выполнению
Использовать радикальный признак Коши ( теорема 1.8 на стр. 36).
При этом полезно иметь в виду следующий предел:
Ñ Пример выполнения задания.
(См. также:
§ пример I.1. - 5 (Исследование рядов на сходимость с помощью радикального признака Коши) на стр. 37).
Исследовать на сходимость ряд
.
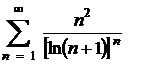Решение
По признаку Коши,
сходимость ряда определяется в зависимости от величины
предела
.
А именно:
1) если , то ряд сходится;
2) если , то ряд расходится;
3) если , то в этом случае требуется дополнительное исследование ряда с помощью других методов.
Исследуем с помощью признака Коши ряд (1)
Найдем предел 
.
Имеем:
,
так как:
.
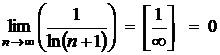Получили:
исследуемый ряд 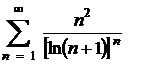сходится по признаку Коши.
Итак, ряд
