Исследуем сходимость ряда (1) с помощью достаточного признака сходимости

Теоретические упражнения

Группа А (Базовые упражнения)

1. Ряды и сходятся. Доказать, что ряд сходится, если выполняется условие: .

Указание.

Использовать неравенства .

2. Ряд сходится. Доказать, что ряд тоже сходится. Показать (на примере), что обратное утверждение неверно.

3. Пусть ряд сходится, и . Можно ли утверждать, что ряд тоже сходится?

Рассмотреть пример: и .

4. Пусть ряд сходится равномерно на отрезке 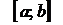. Доказать, что ряд также сходится равномерно на этом отрезке.

Группа Б (Дополнительные упражнения)

5. Доказать, что , исследовав на сходимость ряд .

6. Привести пример двух рядов и , для которых ряд сходится, а ряд расходится.

7. Доказать, что если знакопеременный ряд сходится абсолютно, то и ряд сходится абсолютно.

8. Доказать, что если ряд сходится абсолютно, то и ряд, полученный из исходного с помощью произвольной перестановки его членов, также сходится абсолютно, причем к той же сумме, что и исходный ряд.

9. Существует ли степенной ряд, для которого верно следующее утверждение:

а) на обоих концах интервала сходимости ряд расходится;

б) на одном конце интервала сходимости ряд сходится условно, а на другом — сходится абсолютно;

в) на обоих концах интервала сходимости ряд сходится абсолютно.

Расчетные задания

Группа А (Базовые задания)

Задача 1. Найти сумму ряда.

(См.: п. I.1.1. Числовой ряд, сходимость и сумма ряда, простейшие свойства рядов, необходимый признак сходимости).

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.10

1.11

1.12

1.13

1.14

1.15

1.16

1.17 .	1.18 .
1.19 .	1.20 .

1.21

1.22

1.23

1.24

1.25

1.26

1.27

1.28

1.29

1.30

1.31

Указание к выполнению

1. Разложить общий член ряда на элементарные дроби, т.е. представить в виде:

2. Выписать несколько частичных сумм ряда так, чтобы было видно, какие слагаемые при этом сокращаются (см. определение 1.2, формулы (1.2) – (1.3) на стр. 7).

3. Найти частичную сумму ряда (т.е. сумму первых членов ряда), сократив соответствующие слагаемые.

4. Вычислить сумму ряда по формуле: (см. (1.5) на стр. 7).

Ñ Пример выполнения задания.

Найти сумму ряда .

Решение

Разложим общий член ряда на элементарные дроби.

Имеем:

Подставляя найденные значения и в разложение (2), получаем:

Выпишем несколько частичных сумм ряда: — так, чтобы было видно, какие слагаемые при этом сокращаются.

Так как в нашем случае суммирование начинается с (т.е. можно считать ), имеем:

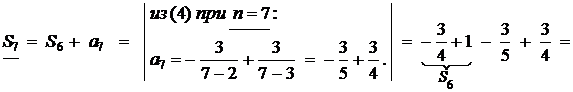
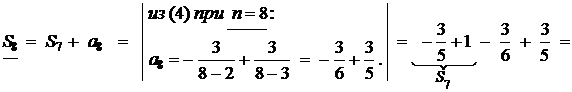
Вычислим сумму ряда по формуле: .

Получаем: .

Итак, окончательно получили:

Сумма ряда равна.

Задача 2. Исследовать на сходимость ряд.

(См.:

§ п. I.1.1. Числовой ряд, сходимость и сумма ряда, простейшие свойства рядов, необходимый признак сходимости.

§ п. I.1.2. Ряды с положительными членами. Достаточные признаки сходимости рядов с положительными членами: первый и второй признаки сравнения, признак Даламбера, радикальный признак Коши, интегральный признак).

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

2.9

2.10

2.11

2.12

2.13

2.14

2.15

2.16

2.17 .	2.18 .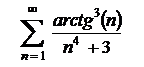
2.19 .	2.20 .

2.21

2.22

2.23

2.24

2.25

2.26

2.27

2.28

2.29

2.30

2.31

Указание к выполнению

Использовать:

§ необходимый признак сходимости ( теорема 1.4 на стр. 9);

§ первый признак сравнения ( теорема 1.5 настр. 16).

В качестве эталонных рядов (для сравнения с исследуемыми рядами) использовать ряды из приложения 2.

Ñ Пример выполнения задания.

(См. также:

§ пример I.1. – 1 (Исследование рядов на сходимость с использованием определениясходимости, простейших свойств рядов и необходимого признака сходимости), случай 2 а) на стр. 14;

§ пример I.1. - 2 (Исследование рядов на сходимость с помощью первого признака сравнения) на стр. 17.)

Исследовать на сходимость ряд

Решение

1. Согласно необходимому признаку сходимости,

§ если , то ряд расходится;

§ если же , то ряд может быть

как сходящимся, так и расходящимся — требуется дальнейшее исследование сходимости с помощью достаточных признаков (например, по первому признаку сравнения).

Найдем предел общего члена ряда (1):