Радиус-вектор.
Материалдық нүктенің қозғалысын сипаттау дегеніміз ке-келген уақыт мезетіндегі оның кеңістіктегі орынын көрсету деген сөз. Ол өзінің қозғалысы кезінде үздіксіз нүктелер жиынтығын траекторияны қалдырады.
Санақ жүйесіндегі нүктенің орнын әр түрлі әдіспен беруге болады.
Қозғалысты координаталық формада беру. Қозғалыс кезінде оның координаталары (x1=x, x2=y, x3=z) уақыт бойынша өзгереді, яғни уақыттың функциясы болып табылады. Қозғалысты беру –осы функцияларды көрсету:
x1=x1(t), x2=x2(t), x3=x3(t)
Қозғалысты векторлық формада беру. Қозғалыс кезінде оның радиус-векторы үнемі өзгеріп отырады. Қозғалыс мынандай түрде беріледі:
= (t) (1.1)
Қозғалысты траектория параметрлері арқылы беру. Егер траектория берілсе, онда қозғалыс заңдары оның айналасында анықталады. Траекторияның қайсы бір нүктесі қозғалыс басы ретінде алынады, ал одан S ара қашықтағы нүкте:
S = S(t). (1.2)
Орын ауыстыру векторы. Орын ауыстыру векторы 
= (t+ t) – (t) бастапқы және соңғы нүтелерді қосатын бағытталған кесіндімен анықталады. Ол кесінділердің орыны t және t+ t. Уақыт мезеттеріне сәйкес келеді.
Сурет. 1.1
Жылдамдық. Орташа жылдамдық векторы 
мынаған тең:
(1.3)
Лездік жылдамдық.
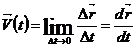(1.4)
Декарттық координат жүйесінде:
= 
= 
+ 
+ 
,
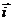
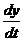мұндағы 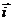, , - бірлік өлшем бірліксіз векторлар, x, y, z остері бағыттарымен бағытталған.
Траекторияға жанама бойымен бағытталған лездік жылдамдық(сурет. 1):
= 
v,
мұндағы – траекторияға жанама бірлік вектор
Үдеу. t уақыттағы орташа үдеу мынаған тең:
(t, t+ t) = 
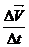(1.5)
жылдамдық годографы (сурет. 2):
сурет. 2.2
t 
0 кезде, үдеу:
= 
= 
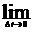
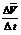(1.6)
Декарттық координат жүйесінде:
= 
+ 
+ 
.
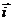
Толық үдеу. өзара перпендикуляр екі құраушыдан тұрады: тангенциальдық үдеу
(
) = 
және нормаль үдеу 
= 
:
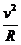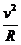= + () (1.7)
Толық үдеу модулі:
(1.8)
Айналмалы қозғалыс. Бұрыштық жылдамдық векторы. Қатты дененің айналмалы қозғалысы бұрыштық жылдамдық шамасымен анықталады. Модулі бойынша ол w = 
және 
сызықтық жылдамдық жанама бойынша бағытталатындай бағытта бағытталған:
= 
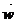
, (1.9)
Сурет. 2.3.
Элементар бұрыштық орын ауыстыру векторы. Элеменртар бұрыштық орын ауыстыру векторы: 
. Соондықтан бұрыштық жылдамдық:
= 
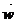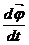(1.10)
Бұрыштық үдеу. Бұрыштық жылдамдық уақыт бойынша туындысы 
бұрыштық үдеу деп аталады:
= (1.11)
Бұрыштық жылдамдық пен бұрыштық үдеудің өлшем-бірліктері – рад / с и рад / с2.
2. Термодинамиканың екінші бастамасы. Энтропия. Қайтымды және қайтымсыз процесстер. Айналмалы циклдің ПӘК-і.
Термодинамиканың екінші бастамасының кейбір тұжырымдамалары
1. Тұйық жүйелерде өтетін қайтымсыз процестерде жүйенің энтропиясы ұлғаяды.
2. Нәтижесі тек қыздырғыштан алынған жылуды оған эквивалентті жұмысқа түрлендіруде ғана болатын дөңгелек процестің өтуі мүмкін емес (Кельвин).
3. Нәтижесі тек салқын денеден ыстық денеге жылудың берілуінде ғана болатын процестің өтуі мүмкін емес (Клаузиус).
Термодинамиканың екінші бастамасы — статистикалық нысандардың (мысалы, атом, молекулалардың) үлкен санынан тұратын жүйелердің өз бетінше ықтималдығы аздау күйден ықтималдығы молырақ күйге ауысу процесін сипаттайтын табиғаттың түбегейлі заңы
Энтропия (гр. еntropіa – бұрылыс, айналу) – тұйық термодинамикалық жүйедегі өздігінен жүретін процестің өту бағытын сипаттайтын күй функциясы. Энтропияның күй функциясы екендігі термодинамиканың екінші бастамасында тұжырымдалады. Энтропия ұғымын термодинамикаға 1865 ж. Р.Клаузиус енгізген
