Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, пределов функций, определенных интегралов, находят приближенные решения дифференциальных уравнений.
Остановимся на применении степенных рядов к приближенным вычислениям определенных интегралов.
Многие определенные интегралы, получающиеся при решение практических задач, не могут быть вычислены с помощью формулы Ньютона-Лейбница, поскольку применение этой формулы связано с нахождением первообразной, которая не всегда выражается в элементарных функциях.
Если, однако, подынтегральная функция разлагается в степенной ряд, а отрезок интегрирования входит в область сходимости этого ряда, то возможно приближенное вычисление интеграла с любой заданной точностью.
Пусть требуется вычислить приближенно определенный интеграл 
с заданной точностью ε.. Для этого необходимо:
- подынтегральную функцию разложить в степенной ряд, указав область сходимости;
- убедившись, что отрезок интегрирования [ a, b ]входит в область сходимости ряда, проинтегрировать обе части этого равенства, причем правую часть проинтегрировать почленно. В результате, в простейших случаях, получается знакочередующийся числовой ряд, удовлетворяющий условиям теоремы Лейбница, т.е. сходящийся ряд;
- в качестве приближенного значения интеграла берем значение частичной суммы Sn, число п определяется из условия, что ошибка при замене суммы ряда его частичной суммой по абсолютной величине не превосходит первого из отброшенных членов ряда.
Пример 28
Вычислить приближенно интеграл 
с точностью ε= 0,1.
Решение.
Данный интеграл относится к неберущимся интегралам. Однако подынтегральная функция разлагается в степенной ряд. Используем известное разложение в ряд Маклорена
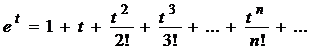при t Î(–¥,+¥);
Полагая t = -х 2, получим разложение подынтегральной функции в степенной ряд
при х Î(–¥,+¥);
Так как отрезок интегрирования [0;1]входит в область сходимости, то в этих пределах можно проинтегрировать обе части последнего равенства (ряд интегрируем почленно):
Получили числовой знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница. Так как модуль четвертого члена ряда меньше заданной точности ε = 0,1,т.е. 
, значит, членами ряда, начиная с четвертого, можно пренебречь. Таким образом, заданная точность обеспечивается первыми тремя членами ряда, т.е.
.
Пример 29
Вычислить приближенно интеграл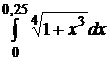 
с точностью ε =0,0001.
Решение.
Используя биномиальное разложение функции (1 + t) m, полагая в нем 
и 
,получим разложение подынтегральной функции в степенной ряд
при 
.
Так как отрезок интегрирования [0; 0,25] входит в область сходимости, то обе части последнего равенства можно проинтегрировать (правую часть почленно) по заданному отрезку, в результате получим
Заметим, что уже третий член ряда по абсолютной величине не превосходит заданной точности е = 0,0001,т.е. 
.
Следовательно, для обеспечения заданной точности е достаточно взять первых два члена полученного числового ряда.
.
