Постановка задачи. Ряд Тейлора
В теории функциональных рядов центральное место занимает раздел, посвященный разложению функции в ряд.
Таким образом, ставится задача: по заданной функции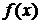 
требуется найти такой степенной ряд
,
который на некотором интервале сходился и его сумма была равна 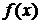, т.е.
= ..
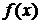Эта задача называется задачей разложения функции в степенной ряд.
Необходимым условием разложимости функции в степенной ряд является её дифференцируемость бесконечное число раз – это следует из свойств сходящихся степенных рядов. Такое условие выполняется, как правило, для элементарных функций в их области определения.
Итак, предположим, что функция 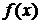имеет производные любого порядка. Можно ли её разложить в степенной ряд, если можно, то как найти этот ряд? Проще решается вторая часть задачи, с неё и начнем.
Допустим, что функцию 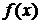можно представить в виде суммы степенного ряда, сходящегося в интервале, содержащем точку х 0:
= .. (*)
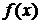где а 0 ,а 1 ,а 2 ,,...,ап,... – неопределенные (пока) коэффициенты.
Положим в равенстве (*) значение х = х 0, тогда получим
.
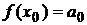Продифференцируем степенной ряд (*) почленно
= 
..
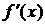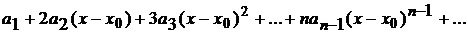и полагая здесь х = х 0,получим
.
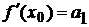При следующем дифференцировании получим ряд
= 
..
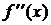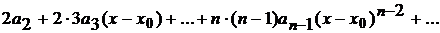полагая х = х 0,получим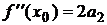 
, откуда 
.
После п -кратного дифференцирования получим
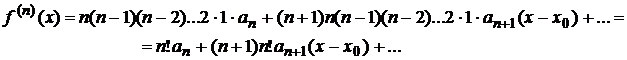
Полагая в последнем равенстве х = х 0,получим 
, откуда
Итак, коэффициенты найдены
, 
, 
, …, ,….,
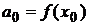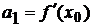подставляя которые в ряд (*), получим
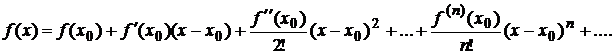
Полученный ряд называется рядом Тейлора для функции .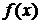
Таким образом, мы установили, что если функцию можно разложить в степенной ряд по степеням (х - х 0 ), то это разложение единственно и полученный ряд обязательно является рядом Тейлора.
Заметим, что ряд Тейлора можно получить для любой функции, имеющей производные любого порядка в точке х = х 0. Но это еще не означает, что между функцией и полученным рядом можно поставить знак равенства, т.е. что сумма ряда равна исходной функции. Во-первых, такое равенство может иметь смысл только в области сходимости, а полученный для функции ряд Тейлора может и расходиться, во-вторых, если ряд Тейлора будет сходиться, то его сумма может не совпадать с исходной функцией.
Достаточные условия разложимости функции в ряд Тейлора
Сформулируем утверждение, с помощью которого будет решена поставленная задача.
Если функция 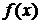в некоторой окрестности точки х 0 имеет производные до (n + 1 )-го порядка включительно, то в этой окрестности имеет место формула Тейлора
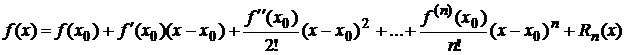
где Rn (х) -остаточный член формулы Тейлора – имеет вид (форма Лагранжа)
где точка ξ лежит между х и х 0.
Отметим, что между рядом Тейлора и формулой Тейлора имеется различие: формула Тейлора представляет собой конечную сумму, т.е. п - фиксированное число.
Напомним, что сумма ряда S (x) может быть определена как предел функциональной последовательности частичных сумм S п (x)на некотором промежутке Х:
.
Согласно этому, разложить функцию в ряд Тейлора означает найти такой ряд, что для любого х Î X
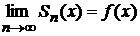
Запишем формулу Тейлора в ви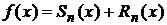де 
, где
.
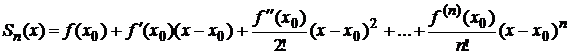Заметим, что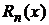 
определяет ту ошибку, которую мы получаем, заменяй функцию f (x) многочленом Sn (x).
Если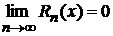 
, то 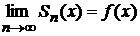, т.е. функция разлагается в ряд Тейлора. Инаоборот, если 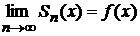, то .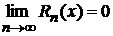
Тем самыммы доказали критерий разложимости функции в ряд Тейлора.
Для того, чтобы в некотором промежутке функция f (х) разлагалась в ряд Тейлора, необходимо и достаточно, чтобы на этом промежутке 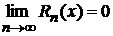, где Rn (x) - остаточный член ряда Тейлора.
С помощью сформулированного критерия можно получить достаточные условия разложимости функции в ряд Тейлора.
Если в некоторой окрестности точки х 0 абсолютные величины всех производных функции ограничены одним и тем же числом М ≥ 0, т.е.
, т о в этой окрестности функция разлагается в ряд Тейлора.
Из вышеизложенного следует алгоритм разложения функции f (x) в ряд Тейлора в окрестности точки х 0:
1. Находим производные функции f (x):
f(x), f’(x), f”(x), f’”(x), f(n) (x),…
2. Вычисляем значение функции и значения её производных в точке х 0
f(x0), f’(x0), f”(x0), f’”(x0), f(n) (x0),…
3. Формально записываем ряд Тейлора и находим область сходимости полученного степенного ряда.
4. Проверяем выполнение достаточных условий, т.е. устанавливаем, для каких х из области сходимости, остаточный член Rn (x) стремится к нулю при 
или .
Разложение функций в ряд Тейлора по данному алгоритму называют разложением функции в ряд Тейлора по определению или непосредственным разложением.