функций
Частный случай ряда Тейлора при х 0 =0
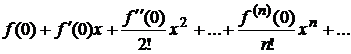
н азываемся рядом Маклорена для функции f (x).
Найдем разложение некоторых элементарных функций в ряд Маклорена.
Пример 23
Разложить в ряд Маклорена функцию 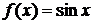 .
.
Решение.
Для решения задачи будем использовать алгоритм, сформулированный выше. Так как требуется разложить функцию в ряд Маклорена, следовательно, будем искать разложение в окрестности точки х 0 = 0.
Найдем значение функции в точке х 0 =0, производные функции до п -го порядка и их значения при х 0 = 0:
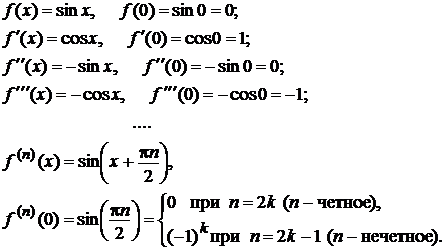
Запишемформально ряд Маклорена по формуле
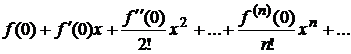 ,
,
получим
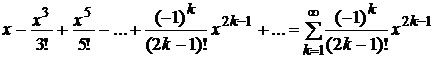 .
.
Заметим, что получили рад по нечетным степеням, так как коэффициенты при четных степенях (когда п - четное число) равны нулю.
Найдем область сходимости полученного ряда, для этого составим ряд из абсолютных величин членов ряда:

и применим к нему признак Д'Аламбера.
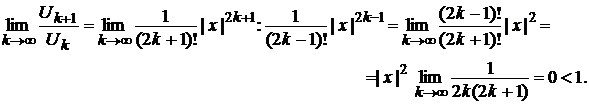
Так как величина предела не зависит от х и меньше единицы при любом х, то ряд сходится при всех значения, значит, область сходимости ряда х Î(–¥,+¥).
Проверим выполнение достаточных условий. Очевидно, что
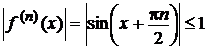 для п = 0,1,2,... и для любых х,
для п = 0,1,2,... и для любых х,
значит, функция разлагается в свой ряд Маклорена на всей числовой оси, т.е.

при х Î(–¥,+¥).
В рассмотренном примере для определения коэффициентов разложения функции в степенной ряд в окрестности точки х 0=0 мы последовательно дифференцировали функцию до тех пор, пока не смогли вывести формулу для п -ой производной, и находили значения производных в данной точке. Затем выясняли, для каких х выполняются достаточные условия разложимости функции в ряд. Часто эти шаги приводят к громоздким вычислениям. Эти трудности иногда можно обойти, используя утверждение о том, что полученное любым способом разложение функции в степенной ряд будет её разложением в ряд Тейлора. Поэтому, чтобы получить разложение функции в степенной ряд, можно использовать уже известные разложения элементарных функций ряд Маклорена, применяя к ним правила сложения, умножения рядов и теоремы об интегрировании и дифференцировании степенных рядов.
Например, разложение функции f (x)= cos x можно получить, продифференцировав почленно разложение в ряд Маклорена функции f (x) = sin x.
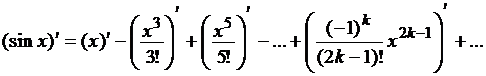 ,
,
 при х Î(–¥,+¥).
при х Î(–¥,+¥).
Аналогично, используя алгоритм разложения и теоремы об интегрировании и дифференцировании степенных рядов, можно получить разложения в ряд Маклорена следующих элементарных функций:
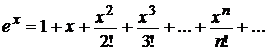 при х Î(–¥,+¥);
при х Î(–¥,+¥);
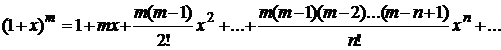 ,
,
е сли т≥.0, или т £ -1, то область сходимости х Î (- 1;1),
е сли –1< т<0, то область сходимости х Î (- 1;1].
Такое разложение называется биномиальным рядом. В частности, полагая в последнем разложении т = –1, получим
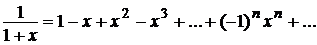 , х Î (-1;1).
, х Î (-1;1).
Заменяя в этом разложении х на выражение (– х), получим
 , при х Î (–1;1).
, при х Î (–1;1).
Используя теорему об интегрировании степенных рядов и применяя её к разложению в ряд Маклорена функции 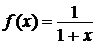 , получим
, получим
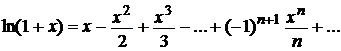 при х Î (–1;1].
при х Î (–1;1].
Заменяя в разложении функции 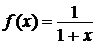 переменную х на выражение
переменную х на выражение 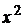 и интегрирую, получим
и интегрирую, получим
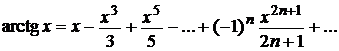 , при х Î [–1;1].
, при х Î [–1;1].
Используя биномиальный ряд– разложение в ряд Маклорена функции 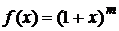 , полагая
, полагая 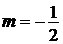 , заменяя х на выражение
, заменяя х на выражение 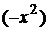 и интегрируя, получим
и интегрируя, получим
 , при х Î (–1;1).
, при х Î (–1;1).
Пример 24.
Используя известные разложения, разложитьв ряд Мэклорена функцию  .
.
Решение
Необходимо найти разложение функции в ряд Маклорена, т.е. в степенной ряд по степеням х. Будем использовать разложение
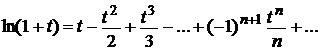 при t Î (–1;1].
при t Î (–1;1].
Полагая t = x 2, получим

Это разложение справедливо, когда 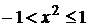 , откуда
, откуда 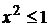 , тогда область сходимости
, тогда область сходимости  .
.
Таким образом,

Умножая обе части равенства на х, получим
 при х Î [–1;1].
при х Î [–1;1].
Пример 25
Используя известные разложения, разложись функцию 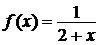 в ряд Тейлора в окрестности точки х 0 =1.
в ряд Тейлора в окрестности точки х 0 =1.
Решение.
Необходимо получить разложение функции в ряд Тейлора в окрестноститочки х 0 = 1, т.е. по степеням (х –1).
Будем использовать разложение
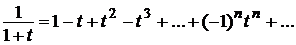 , при t Î (-1;1).
, при t Î (-1;1).
Для того, чтобы получить разложение данной функции по степеням (х –1)введем новую переменную t = x –1, тогда х = t + 1.Преобразуем данную функцию к новой переменной, полагая х = t + 1:
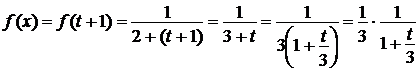
Полагая в известном разложении вместо t выражение 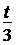 и умножая на число
и умножая на число  , получим
, получим
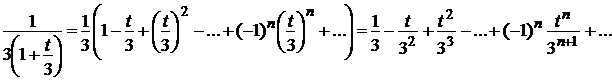 ,
,
при 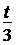 Î (-1;1).
Î (-1;1).
Полагая в полученном разложении t = x –1,возвратимся к исходной переменной х и получим разложение данной функции в степенной ряд по степеням (х -1):
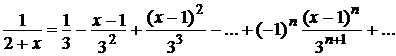
Это разложение справедливо при условии 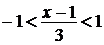 , откуда
, откуда 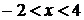 .
.
Итак, получили разложение
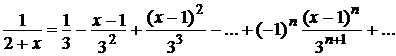 при
при 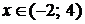 .
.
Пример 26
Разложить функцию 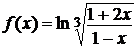 в степенной ряд в точке
в степенной ряд в точке  .
.
Решение.
Преобразуем данную функцию, используя свойства логарифмов:
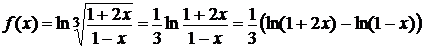
Используя известное разложение
 при t Î (–1;1].
при t Î (–1;1].
найдем разложение функции 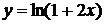 ,полагая t = 2 x, и функции
,полагая t = 2 x, и функции 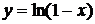 , полагая t = –х:
, полагая t = –х:
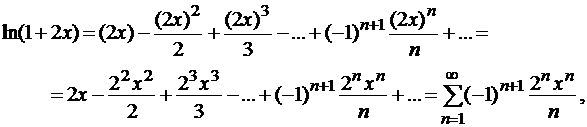
разложение справедливо при 2 х Î (–1;1),т.е. при  .
.
Аналогично,
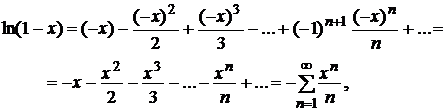
и разложение справедливо при (– х) Î (–1;1), т.е. при х Î (–1;1).
Степенные ряды можно почленно складывать и умножать на число, значит


 причем это разложение справедливо на общей области сходимости, т.е. при
причем это разложение справедливо на общей области сходимости, т.е. при  .
.
П ример 27
Разложить в ряд Маклорена функцию  .
.
Решение.
Преобразуем функцию
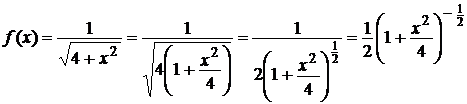 .
.
Используя известное разложение в ряд Маклорена функции у =(1 + t) m, полагая 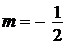 и
и 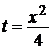 , получим
, получим
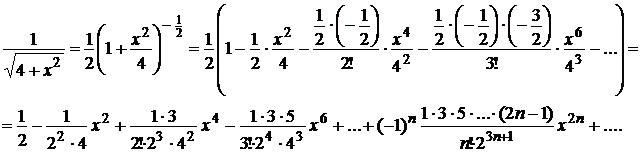
Используемый биномиальный ряд при 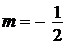 имеет область сходимости t Î (-1;1], следовательно, полученное разложение справедливо при
имеет область сходимости t Î (-1;1], следовательно, полученное разложение справедливо при  , откуда
, откуда 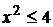 ,
, 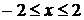 .
.
Итак, 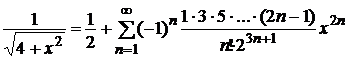 при
при 
 .
.




