Знакопеременный ряд, знаки членов которого чередуются
называется знакочередующимся рядом.
Для исследования сходимости знакочередующегося ряда используют признак Лейбница.
Теорема (признак Лейбница)
Если в знакочередующемся ряде
члены таковы, что
1) 
начиная хотя бы с некоторого номера п0,
2) 
,
то знакочередующийся ряд сходится, причем его сумма положительна и не превосходит первого члена ряда, т.е.
.
Если знакочередующийся ряд удовлетворяет условиям признака Лейбница, то можно оценить ошибку, которая получается, если заменить его сумму S частичной суммой 
. При такой замене мы отбрасываем все члены ряда, начиная с 
. Но эти отброшенные слагаемые сами образуют сходящийся знакочередующийся ряд, сумма которого, согласно теореме Лейбница, по абсолютной величине не превосходит первого члена этого ряда, т.е. меньше :
, где 
Значит, ошибка, допускаемая при замене 
на , не превосходит по абсолютной величине первого из отбрасываемых членов.
Пример 14.
Доказать, что ряд 
сходится и вычислить приближенно значение его суммы с точностью до 
=0,01.
Решение.
Данный ряд – знакочередующийся. Для исследования его сходимости используем признак Лейбница. Проверим выполнение условий теоремы:
1) Докажем, что при любом п (или начиная с некоторого номера). Для данного ряда имеем
,
Þ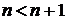 
Þ 
Þ 
получили неравенство, которое верно для любого п, значит, верно и неравенство для любого п.
2) Проверим условие : 
.
Таким образом, оба условия теоремы Лейбница выполнены, следовательно, ряд сходится.
Как отмечалось выше, ошибка, допускаемая при замене точного значения суммы ряда на приближенное значение частичной суммы , не превосходит по абсолютной величине первого из отбрасываемых членов. Значит, чтобы вычислить сумму ряда с указанной точностью, нужно найти такой член ряда, который по абсолютной величине меньше заданной точности и начиная с этого члена отбросить остаток ряда. Затем вычислить оставшуюся частичную сумму – она и будет равна сумме ряда с заданной точностью =0,01.
Для данного ряда имеем:
,
следовательно, для вычисления суммы ряда с точностью =0,01, достаточно взять первых три члена ряда.
.
При этом допущенная ошибка не превосходит первого отброшенного члена, т.е.
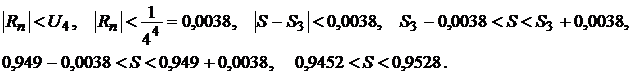
Пример 15.
Исследовать сходимость ряда и установить характер сходимости (абсолютная или условная).
а) 
;
б) 
;
в) 
;
г) 
Решение.
а) Составим ряд из абсолютных величин членов данного ряда:
.
Получили гармонический ряд – он расходится. Но сделать вывод о сходимости заданного знакочередующегося ряда нельзя. Он точно не является абсолютно сходящимся, т.к. ряд из абсолютных величин расходится. Но он может сходиться условно или расходиться. Проверим это с помощью признака Лейбница.
1) Имеем 
. Проверим условие :
– получили неравенство, верное для любого п, значит, для любого п.
2) Условие также выполняется: 
.
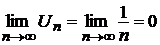Следовательно, данный знакочередующийся ряд 
сходится по признаку Лейбница. А так как ряд, составленный из абсолютных величин его членов, расходится, то данный ряд сходится условно.
б) Для знакочередующегося ряда составим ряд из абсолютных величин его членов:
.
Применим к этому ряду признак Д¢Аламбера.
,
значит, ряд составленный из абсолютных величин членов заданного ряда, сходится. А это значит, что и заданный ряд сходится, причем абсолютно.
в) К знакочередующемуся ряду 
применим признак Лейбница.
1) Проверим выполнение условия :
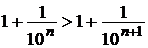Þ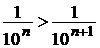 
Þ 
Þ
(разделим обе части неравенства на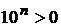 
) Þ 
– получили неравенство, верное для любого п, следовательно, для любого п выполняется и неравенство .
2) Проверим условие : 
, т.е. второе условие признака Лейбница не выполняется, следовательно, данный ряд расходится.
г) Для ряда составим ряд из абсолютных величин его членов:
.
Общий член полученного ряда представляет собой отношение двух многочленов, поэтому для исследования его сходимости целесообразно применить предельный признак сравнения. В качестве «эталонного» ряда возьмем гармонический ряд 
, который расходится. Найдем предел отношения общих членов этих рядов:
.
Значит, оба ряда ведут себя одинаково и следовательно, ряд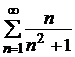 
расходится.
Таким образом, пока ничего нельзя сказать о сходимости исходного знакочередующегося ряда, он может расходиться или сходиться условно.
Применим к заданному ряду признак Лейбница.
1) Проверим выполнение условия :
Þ 
Þ 
Þ 
.
Очевидно, что при любом значении п знаменатель дроби 
, значит, числитель дроби тоже больше нуля:
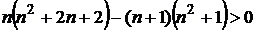Þ 
Þ
.
Очевидно, полученное неравенство верно для любого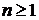 
, следовательно, для любого п выполняется и неравенство .
2) Проверим условие : 
, т.е. второе условие признака Лейбница также выполняется, следовательно, данный ряд сходится. А так как ряд из абсолютных величин его членов расходится, то заданный ряд сходится условно.
*) Здесь использован второй замечательный предел.
*) Здесь мы воспользовались известным неравенством для всех.
*) Здесь использован первый замечательный предел.
