Основные теоретические сведения и примеры решения типовых задач
Тема 1 Числовые ряды.
Основные определения. Свойства сходящихся рядов. Необходимый признак сходимости
Напомним:
Числовой последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расположенных в порядке возрастания номеров, т.е.
Примерами числовых последовательностей являются известные из школьного курса:
арифметическая прогрессия
,
где а – первый член прогрессии, 
– разность прогрессии;
а так же бесконечная геометрическая прогрессия
,
где а –первый член прогрессии, q – знаменатель прогрессии.
Последовательность считается заданной, если известен закон, по которому можно вычислить любой её член 
при заданном п.
Например, для арифметической прогрессии п -й член определяется по формуле 
для любого 
, для геометрической прогрессии формула общего члена 
.
Если 
, то её первый член 
, второй – 
, и т.д., а сама последовательность имеет вид:
,…
Пусть задана некоторая бесконечная последовательность чисел:
Выражение вида 
называют числовым рядом и обозначают
= .
Числа называют членами ряда, а выражение – общим или п-ным членом ряда.
Примеры рядов:
· 
, здесь = 
;
· 
, здесь = 
;
· Ряд геометрической прогрессии со знаменателем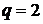 
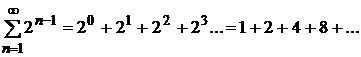, здесь = 
.
Сумма первых п членов числового ряда называется п-ой частичной суммой и обозначается S n.
.
Таким образом, частичные суммы сами образуют числовую последовательность.
Если существует конечный предел последовательности п-ых частичных сумм числового ряда, равный S, т.е.
,
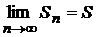То числовой ряд называется сходящимся, а число S – суммой ряда.
Пример 1
Используя определение, исследовать сходимость ряда:
а) 
,
б)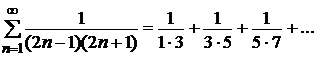 
.
Решение.
а) Рассмотрим последовательность частичных сумм данного ряда:
.
Очевидно, Sn принимает значения 1, если число слагаемых нечетное, и значение 0, если число слагаемых четное. Такая последовательность частичных сумм предела не имеет, следовательно, ряд расходится.
б) Рассмотрим последовательность частичных сумм ряда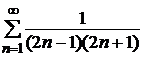 
:
Для упрощения вычислений таких сумм заметим, что общий член данного ряда
есть правильная рациональная дробь и её можно разложить на простейшие дроби. Выполнив это разложение, получим
,
т.е. каждое слагаемое частичных сумм данного ряда можно записать в виде разности двух дробей:
Тогда
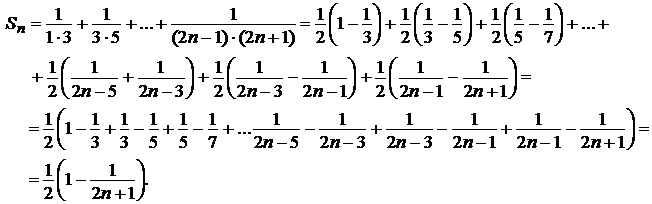Найдем предел последовательности частичных сумм:
.
Таким образом, последовательность частичных сумм имеет конечный предел, значит, ряд сходится и его сумма равна 
.
Пример 2.
Исследовать сходимость ряда 
.
Решение.
Данный ряд составлен из членов бесконечной геометрической прогрессии с первым членом а (а ¹0) и знаменателем q.
Из школьного курса математики известно, что сумма 
первых п членов геометрической прогрессии находится по формуле
.
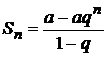Найдем предел частичных сумм данного ряда:
.
Величина этого предела зависит от значения q. Действительно:
1) если 
, то 
и тогда
,
следовательно, существует предел частичных сумм и значит, ряд сходится, а его сумма равна 
;
2) если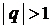 
то 
и тогда
,
Значит, в этом случае ряд расходится, и суммы не имеет;
3) если q =1, то ряд принимает вид
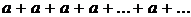
В этом случае 
и 
, следовательно, ряд расходится;
4) если q = –1, то ряд принимает вид
.
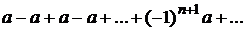При этом 
В таком случае 
не существует и следовательно, ряд расходится.
Итак, можно сделать вывод, что ряд геометрической прогрессии
В качестве примера можно привести ряд 
, который сходится, поскольку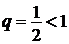 
, и ряд 
, который расходится, так как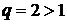 
(в обоих случаях, а =1).
Основные свойства числовых рядов
1. Если сходится ряд 
, то сходится и ряд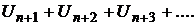 
, полученный из данного отбрасыванием первых п членов.
Ряд 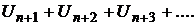называют п-ым остатком ряда и обозначают 
. Из сходимости остатка ряда следует сходимость самого ряда.
Иными словами, отбрасывание конечного числа членов ряда или добавление конечного числа членов не влияет на сходимость (расходимость) ряда (сумма сходящегося ряда при этом, конечно, меняется)
2. Если ряд сходится и его сумма равна S, то 
. Отсюда следует, что
1) при достаточно большом п 
;
2) есть погрешность, допускаемая при замене суммы S ряда его п-ой частичной суммой S п.
3. Если сходится ряд и его сумма равна S, то ряд 
также сходится, причем его сумма равна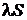 
. Если ряд расходится, то для любого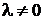 
расходится и ряд .
4. Если ряды и 
сходятся и имеют суммы соответственно 
и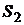 
, то ряд 
также сходится и его сумма равна 
.
При исследовании рядов одним из основных вопросов является вопрос о том, сходится ли данный ряд или расходится. Ответить на этот вопрос можно, конечно же, используя определение, но часто это приводит к сложным вычислениям (пример 1,б). Однако существуют условия, при выполнении которых достаточно просто ответить на вопрос о сходимости ряда. Эти условия налагаются на п-й член ряда и называются признаками сходимости. Ниже мы рассмотрим достаточные признаки сходимости, а также рассмотрим необходимый признак сходимости числового ряда (т.е. условие, при невыполнении которого ряд расходится).
Теорема (необходимый признак сходимости)
Если ряд сходится, то его общий член стремится к нулю при стремлении п к бесконечности, т.е.
.
Доказательство.
По условию теоремы ряд сходится, следовательно, по определению сходящегося ряда 
.
Легко видеть, что 
, тогда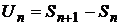 
. Отсюда
,
что и требовалось доказать.
Признак является необходимым для любого ряда, но не является достаточным, т.е. из того, что п -ый член ряда стремится к нулю с увеличением п не следует сходимость самого ряда. Например, известно, что гармонический ряд 
является расходящимся, хотя для него выполняется условие 
.
Из необходимого признака сходимости следует достаточный признак расходимости (для всякого ряда):
Если 
, то ряд расходится.
Пример 3.
Исследовать сходимость ряда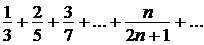 
.
Решение.
Найдем предел общего члена ряда при п, стремящемся к бесконечности:
,
Следовательно, ряд расходится.
Замечание. При решении этого примера и в дальнейшем для раскрытия неопределенности 
полезно помнить, что предел отношения многочленов равен:
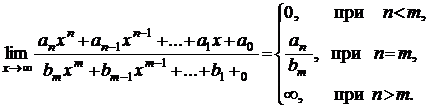
Достаточные признаки сходимости знакоположительных рядов
При изучении знакопостоянных рядов достаточно рассмотреть ряды с положительными членами, причем возможно и существование членов, равных нулю. Ряды с отрицательными членами будем рассматривать как соответствующие ряды с положительными членами, умноженные на (-1), что по свойству рядов не влияет на их сходимость и расходимость.
Числовой ряд
= ,
члены которого неотрицательны, т.е. 
при всех п, называется знакоположительным рядом.
Теорема (признак Д ¢ Аламбера)
Если для знакоположительного ряда
=
отношение последующего члена ряда к предыдущему имеет конечный предел при стремлении п к бесконечности, т.е.
,
то
1) ряд сходится при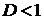 
,
2) ряд расходится при 
.
Замечания:
1.В случае 
ответа на вопрос о сходимости или расходимости ряда теорема не даёт, требуются дополнительные исследования.
2. Если 
, то ряд расходится.
Пример 4.
Исследовать сходимость рядов:
а)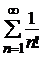 
; б). 
Решение.
Для ответа на поставленный вопрос используем признак Д¢Аламбера.
а) Общий член ряда 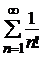имеет вид, тогда. Так как 
, то 
, тогда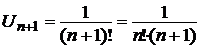 
.
Найдем отношение последующего члена к предыдущему:
.
Тогда
.
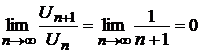Таким образом 
, следовательно, по признаку Д¢Аламбера, данный ряд сходится.
б) Для ряда имеем: 
и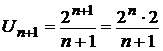 
, откуда
.
Тогда 
, 
, следовательно, ряд расходится согласно признака Д¢Аламбера.
Заметим, что признак Д¢Аламбера дает ответ на вопрос о сходимости знакоположительного ряда только в том случае, когда 
существует и отличен от 1. Если же предел вычислить нельзя или он равен 1, то в этом случае ряд может оказаться и сходящимся, и расходящимся. Для решения вопроса о сходимости таких рядов нужно применить другой признак или определение сходящегося ряда.
Пример 5.
Исследовать сходимость ряда
.
Решение.
Для данного ряда 
и 
, тогда
,
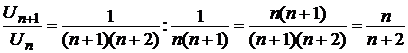откуда
, следовательно, на основании признака Д¢Аламбера сделать вывод о сходимости ряда нельзя. Заметим также, что не дает ответа и необходимый признак, так как
.
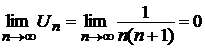Воспользуемся определение сходящегося ряда, т.е. найдем предел последовательности частичных сумм ряда. Для этого, как и в примере 1,б, преобразуем общий член ряда
.
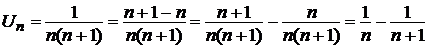Тогда п -ая частичная сумма равна
.
По определению имеем
.
Следовательно, ряд сходится и его сумма равна 1.
Заметим, что признак Д ¢ Аламбера целесообразно применять в том случае, когда в общий член ряда входит показательная функция или (и) п! (факториал). В этом случае обычно 
существует и не равен 1.
Теорема (радикальный признак Коши)
Если для знакоположительного ряда =
величина корня п-ой степени из общего члена имеет конечный предел при стремлении п к бесконечности, т.е.
,
то
1) ряд сходится при 
,
2) ряд расходится при 
.
Замечания:
1.В случае 
ответа на вопрос о сходимости или расходимости ряда теорема не даёт.
2. Если 
, то ряд расходится.
Пример 6.
Исследовать сходимость рядов:
а) 
;
б) 
; в) 
.
Решение.
Для исследования сходимости будем использовать радикальный признак Коши.
а) Для ряда общий член имеет вид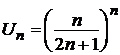 
, тогда
, 
, значит, ряд сходится по признаку Коши.
б) Преобразуем общий член ряда 
:
.
Исследуем сходимость ряда 
. По признаку Коши имеем
.
Согласно замечанию 2 к признаку Коши, ряд расходится, а значит, расходится и ряд 
= .
в) Для ряда имеем:
,
*).
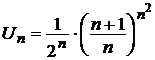Таким образом, 
, следовательно, ряд расходится.
Очевидно, что радикальный признак Коши целесообразно использовать в том случае, когда общий член ряда представляет степень с показателем, кратным п.
Теорема (интегральный признак Коши)
Пусть члены знакоположительного ряда = не возрастают, т.е.
,
и пусть непрерывная невозрастающая функция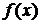 
такова, что 
.
Тогда из сходимости (расходимости) несобственного интеграла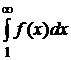 
следует сходимость (расходимость) ряда .
Пример 7.
Исследовать сходимость обобщенного гармонического ряда
в зависимости от р (
).
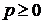Решение.
Очевидно, члены ряда положительны и убывают, т.е.
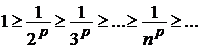
Рассмотрим функцию 
, 
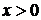. Эта функция удовлетворяет условиям теоремы: 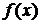не возрастает, непрерывна 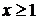при 
, при 
значения функции равны соответствующим членам ряда.
Рассмотрим несобственный интеграл
.
Изучим сходимость этого интеграла при различных значениях р.
1) Если 
, получим
следовательно, несобственный интеграл сходится, а значит, и ряд сходится.
2) Если 
, то
следовательно, несобственный интеграл расходится, и ряд также расходится.
3) Если 
, то
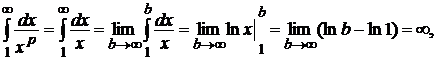
значит, интеграл расходится, и ряд также расходится.
Таким образом, получили, что обобщенный гармонический ряд
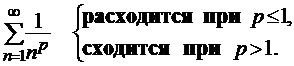
Заметим, что признак Д¢Аламбера и признаки Коши удобны тем, что опираются только на свойства данного ряда. Но часто сходимость или расходимость знакоположительного ряда приходится устанавливать путем сравнения его с другим («эталонным») рядом, заведомо сходящимся или расходящимся. В качестве «эталонного» ряда часто используют ряд, составленный из членов геометрической прогрессии или обобщенный гармонический ряд.
Пксть даны два знакоположительных ряда
= и 
= 
.
Для них справедливы утверждения:
Признак сравнения
Пусть, начиная с некоторого номера п, выполняется неравенство 
. Тогда
1) если ряд сходится, то и ряд – сходится (из сходимости ряда с большими членами следует сходимость ряда с меньшими членами);
2) если ряд расходится, то расходится и ряд (из расходимости ряда с меньшими членами следует расходимость ряда с большими членами).
Предельный признак сравнения
Если существует конечный, не равный нулю предел отношения общих членов двух рядов, т.е. 
, то ряды и либо одновременно сходятся, либо одновременно расходятся.
Пример 8.
Исследовать сходимость ряда 
.
Решение.
Поскольку для всех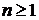 
выполняется условие 
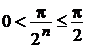, то 
, т.е. заданный ряд – знакоположительный.
Сравним заданный ряд с рядом 
. Члены этого ряда образуют бесконечную геометрическую прогрессию с первым членом 
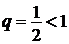и знаменателем , следовательно, этот «эталонный» ряд сходится. Сравним общие члены рассмотренных рядов. Очевидно, что
для любого 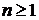*). Таким образом, ряд с большими членами 
сходится, значит, по признаку сравнения, ряд с меньшими членами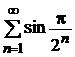 
также сходится.
Для исследования заданного ряда 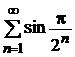на сходимость можно также использовать предельный признак сравнения. В качестве «эталонного» ряда будем использовать тот же ряд членов геометрической прогрессии , который является сходящимся.
Найдем предел отношения общих членов рядов, данного и»эталонного»:
*), получили конечный, не равный нулю предел, значит, заданный ряд ведет себя также, как и выбранный «эталонный» ряд. Следовательно, ряд 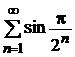сходится.
Пример 9.
Исследовать сходимость ряда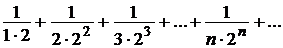 
.
Решение.
Сравним данный ряд со сходящимся рядом 
, составленным из членов бесконечной геометрической прогрессии со знаменателем 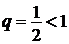. Сравним общие члены этих рядов. Очевидно, для любого 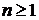имеет место неравенство 
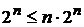, следовательно
.
Таким образом, известно, что ряд с большими членами 
сходится, значит, по признаку сравнения, сходится и ряд 
с меньшими членами.
Заметим, что использование предельного признака сравнения в данном случае не дает ответа на вопрос, т.к. предел отношения общих членов равен нулю:
.
Заметим также, что общий член ряда содержит показательную функцию, поэтому, для исследования сходимости ряда может быть применен признак Д¢Аламбера:
,
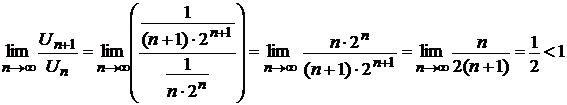следовательно, ряд сходится.
Пример 10
Сходится ли ряд 
?
Решение.
Воспользуемся предельным признаком сравнения. Сравним данный ряд со сходящимся рядом 
, составленным из членов бесконечной геометрической прогрессии со знаменателем 
. Найдем предел отношения общих членов рядов
.
Получили конечный, не равный нулю предел, следовательно, заданный ряд ведет себя так же, как и «эталонный» ряд 
, то есть сходится.
Пример 11.
Исследовать сходимость ряда 
.
Решение.
Сравним данный ряд с гармоническим рядом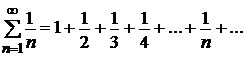 
, который, как известно, расходится.
Применим предельный признак сравнения. Имеем:
, 
,
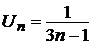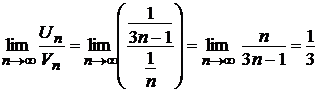, т.е. 
.
Следовательно, заданный ряд, так же как и «эталонный» гармонический, расходится.
Заметим, что применять предельный признак сравнения удобно в том случае, когда общий член исследуемого ряда представляет собой отношение двух многочленов, т.е.
.
В этом случае в качестве «эталонного» используется обобщенный гармонический ряд с общим членом 
, где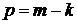 
.
Пример 12.
Исследовать сходимость ряда 
.
Решение.
Общий член данного ряда представляет собой отношение многочленов 
, причем степень числителя 
, а степень знаменателя 
. Учитывая сделанное выше замечание, сравним данный ряд с обобщенным гармоническим рядом с общим членом , где 
, т.е. с гармоническим рядом 
, который расходится. Имеем:
,
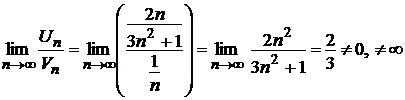следовательно, заданный ряд, как и «эталонный», расходится.
