Определители 2-го порядка, системы 2-х линейных уравнений с двумя неизвестными.
Определение. Число 
, составленное из элементов квадратной матрицы 
, называется определением второго порядка.
Определитель второго порядка обозначают иногда как 
или 
:
.
Например: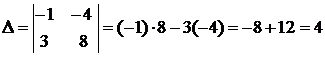 
.
Рассмотрим систему линейных уравнений 
и)составим:
- главный определитель системы,
и 
‑ вспомогательные определители системы.
Вспомогательные определители системы получаются из главного определителя заменой столбца 
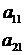коэффициентов при неизвестном 
(в ∆1) и столбца 
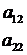коэффициентов при неизвестном 
(в ∆2) столбцом 
свободных членов. Решение системы находим по правилу Крамера: 
, 
(при условии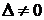 
).
Определители 3-го порядка, системы 3-х уравнений с тремя неизвестными.
Рассмотрим матрицу из девяти элементов (три строки и три столбца):
Первый индекс 
элемента 
обозначает номер строки, второй 
‑ номер столбца.
Определение. Определением третьего порядка называется число, обозначаемое символом
Для запоминания формулы служит геометрическое правило Саррюса. Складываем произведение элементов, расположенных на главной диагонали и на двух треугольниках, с основаниями параллельными главной диагонали и с вершиной на крайнем элементе побочной диагонали:
, 
, 
.
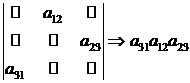Вычитаем произведение элементов, расположенных на побочной диагонали и на двух треугольниках, с основаниями параллельными побочной диагонали и с вершиной на крайнем элементе главной диагонали:
, 
, 
.
Правило Саррюса часто называют так же правилом треугольников и схематично изображают с помощью диаграмм:
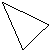
Как и выше, используя определители 3-го порядка, можно по правилу Крамера найти решение системы линейных уравнений
().
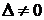Здесь 
‑ соответственно главный определитель и три вспомогательных определителя
, 
, 
, 
.
Вспомогательные определители 
получаются из главного заменой соответственно первого, второго и третьего столбца на столбец правых частей.
Скалярное произведение двух векторов.
Определение. Скалярным произведением двух векторов 
и 
называется число, равное произведению длин векторов на косинус угла меду ними и обозначаемое
или 
.
Если векторы и перпендикулярны, то их скалярное произведение 
. Обратно, если скалярное произведение векторов , то векторы и перпендикулярны.
Зная декартовы координаты векторов и
, 
можно найти их длины
, 
,
скалярное произведение
,
и косинус угла между ними
.
Перечислим основные свойства векторного произведения:
1) 
, (из 
следует 
и обратно);
2) 
(переместительный закон);
3) 
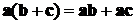(распределительный закон);
4) 
.
