Методические указания к выполнению:
Дифференциальным уравнением первого порядка называется функциональное уравнение (неизвестной является функция), связывающее значения переменной 
, искомой функции 
и ее первой производной 
. Такому уравнению можно придать следующий вид: 
.
Если уравнение может быть записано в виде 
, то оно называется дифференциальным уравнением, разрешенным относительно производной. Функция 
называется решением (частным решением)уравнения на интервале 
, если и только если она дифференцируема на этом интервале, и при подстановке в уравнение функции и ее производной оно обращается в тождество на этом интервале. Если эта функция определяется в неявном виде, т.е. в виде уравнения 
, то такое решение называется интегралом (частным интегралом) дифференциального уравнения.
Общим решением дифференциального уравнения называется функция 
, удовлетворяющая условиям: 1) при любом значении 
из некоторого интервала функция 
является решением уравнения; 2) для любого решения уравнения 
существует и единственно такое значение 
, что 
. Когда общее решение задано неявно уравнением 
, то выражение называется общим интегралом дифференциального уравнения.
Задача Коши состоит в том, чтобы найти такое частное решение уравнения, которое удовлетворяет условию: 
, где 
- заданная точка на интервале , а 
- заданное значение искомой функции.
Общее решение уравнения 
дается формулой 
, где 
- любая из первообразных функций функции 
; 
- произвольная постоянная.
Уравнениями с разделенными переменными называются уравнения первого порядка, записанные в дифференциальной форме, следующего вида: 
. Общий интеграл такого уравнения имеет вид:
(*)
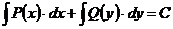Пример 1. Найти общий интеграл уравнения 
.
Решение: Данное уравнение есть ДУ с разделенными переменными. Поэтому его общий интеграл будет иметь вид: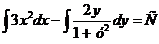 
или 
.■
Уравнения первого порядка, записанные в дифференциальной форме и имеющие следующий вид: 
,
называются уравнениями с разделяющимися переменными.
Они сводятся к уравнениям с разделенными переменными умножением на множитель 
.
Их общий интегралимеет вид: 
Пример 2. Решить уравнение 
.
Решение: Преобразуем левую часть уравнения:
.
Оно является уравнением с разделяющимися переменными. Разделим переменные. Для этого умножим обе части уравнения на множитель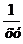 
:
Решением его является общий интеграл 
,т. е. 
.■
Здесь уравнение 
имеет вид 
. Eго решения 
, 
являются решениями данного ДУ, но не входят в общий интеграл. Значит, решения , являются особыми.
Однородными дифференциальными уравнениями называются уравнения первого порядка, которые можно записать в следующем виде:
.
Например, уравнение 
можно записать в виде 
путем деления числителя и знаменателя дроби на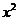 
.
Однородное уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены переменной 
на новую переменную 
соотношением: 
.
Пример 3. Найти общий интеграл уравнения
.
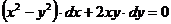Решение: Данное уравнение однородное, т.к. его можно преобразовать к виду 
или 
.
Положим . Тогда 
. Подставляем в исходное уравнение:
,
,
,
последнее — уравнение с разделяющимися переменными. Делим переменные
и интегрируем 
, 
, 
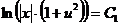обозначим 
, 
. Тогда 
.
Заменяя на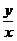 
, получаем: 
— общий интеграл исходного уравнения. ■
Линейными уравнениями называются уравнения первого порядка, которые имеют следующий вид: 
. Решение уравнения методом Бернулли ищется в виде 
, где 
и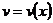 
– неизвестные функции переменного х. Тогда 
. Подставляя выражения и 
в исходное уравнение, получаем: 
или
. (**)
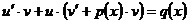Выбирая функцию 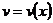так, чтобы выражение в скобках было
равно нулю, решаем уравнение 
. Разделяя переменные и интегрируя, получим:
. Полагая 
, будем иметь 
.
Подставляя найденную функцию 
в уравнение (**), получаем уравнение
.
Решаем его разделением переменных и интегрированием: 
.
Возвращаясь к переменной , получаем общее решение исходного уравнения:
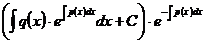
Пример 4. Найти общее решение дифференциального уравнения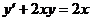 
.
Решение: Полагаем 
. Тогда 
, т. е. 
. Сначала решаем уравнение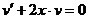 
:
, 
, 
.
Теперь решаем уравнение 
, т. е.
', 
, 
, 
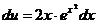Итак, общее решение данного уравнения есть 
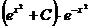т. е. 
. ■
Вопросы для самоконтроля:
- Что называется дифференциальным уравнением первого порядка?
- Что называется решением дифференциального уравнения?
- Сформулировать теорему Коши о существовании и единственности решения уравнения первого порядка.
- Что называется общим и частным решением уравнения первого порядка?
- В чем заключается метод решения уравнения с разделенными переменными?
- Как решить однородное дифференциальное уравнение?
- Раскрыть суть методов решения линейного уравнения первого порядка.
Список литературы:
- Григорьев В.П. Элементы высшей математики: учебник для студ. учреждений сред. проф. образования/ В.П. Григорьев, Ю.А. Дубинский. – 9 – е изд., стер. - М.: Издательский центр «Академия», 2013. – 320 с.
- Григорьев В.П. Сборник задач по высшей математике: учеб. пособие для студ. учреждений сред. проф. образования/ В.П. Григорьев, Т.Н. Сабурова. – 5-е изд., стер. – М.: Издательский центр «Академия», 2014. – 160 с.
- Григорьев В.П. Математика: учебник для студ. учреждений сред. проф. образования/ В.П. Григорьев, Т.Н. Сабурова. – М.: Издательский центр «Академия», 2016. – 368 с.
- Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов. – 3-е изд. перераб. И доп. – М.: Высш. шк.,1990. – 495 с.
