Пусть  и
и 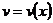 ‒ дифференцируемые функции. Тогда в силу правила дифференцирования произведения функций получим:
‒ дифференцируемые функции. Тогда в силу правила дифференцирования произведения функций получим:
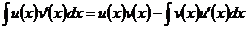 .
.
Эта формула называется формулой интегрирования по частям. Она показывает, что подынтегральную функцию заданного интеграла необходимо представить в виде произведения двух сомножителей, один из которых интегрируют, а другой - дифференцируют. В результате получается более простой интеграл.
Формулу интегрирования по частям удобнее записывать в виде:
 .
.
Пример 5. Найти 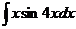 .
.
Решение: Положим 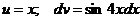 . Тогда
. Тогда 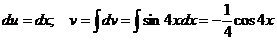 .
.
По формуле интегрирования по частям получим:
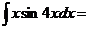
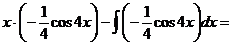
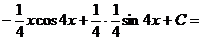
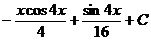 .
.
Вопросы для самоконтроля:
1. Что называется первообразной функции?
2. Сформулировать теорему об общем виде первообразной данной функции.
3. Что называется неопределенным интегралом?
4. Сформулировать основные свойства неопределенного интеграла.
5. В чем суть инвариантности формулы интегрирования?
6. В чем заключается метод непосредственного интегрирования?
7. Проверьте с помощью дифференцирования таблицу основных интегралов.
- Суть интегрирования методом замены переменной?
- В чем заключается метод интегрирования по частям? Записать формулу интегрирования по частям.
- Какие интегралы вычисляют методом интегрирования по частям?
Тема: Определенный интеграл. Вычисление определенных интегралов методом замены переменной и методом интегрирования по частям. Приложение определенного интеграла.
Методические указания к выполнению:
Пусть функция 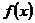 определена на отрезке
определена на отрезке 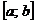 , если произвольно разбить отрезок
, если произвольно разбить отрезок 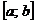 на
на 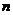 частей, т.е.
частей, т.е.  , то интегральной суммой для функции
, то интегральной суммой для функции 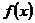
называется сумма вида 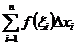 , где
, где  ,
, 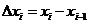 ,
, 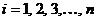 , а определенным интегралом от функции
, а определенным интегралом от функции 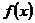 по отрезку
по отрезку 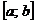 , который обозначается символом
, который обозначается символом 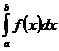 , - предел интегральных сумм, т. е.
, - предел интегральных сумм, т. е.

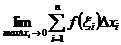 .
.
Если этот предел существует, то функция 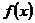 называется интегрируемой по отрезку
называется интегрируемой по отрезку 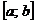 .
.
Необходимое условие существования определенного интеграла:
если функция интегрируема по отрезку 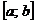 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
Достаточные условия существования определенного интеграла:
если функция 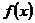 непрерывна на отрезке
непрерывна на отрезке 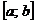 , то она интегрируема по этому отрезку;
, то она интегрируема по этому отрезку;
если функция 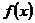 непрерывна на отрезке
непрерывна на отрезке 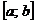 , за исключением конечного числа точек, и ограничена на этом отрезке, то она интегрируема по отрезку
, за исключением конечного числа точек, и ограничена на этом отрезке, то она интегрируема по отрезку 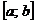 .
.
Свойства определенного интеграла.
1. 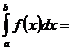
 .
.
2.  .
.
3. 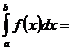
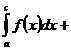
 .
.
4. 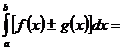
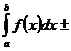
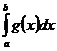 .
.
5. 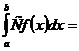
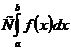 , где
, где 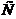 - постоянная.
- постоянная.
6. Если 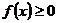 (
(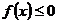 ) для
) для 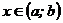 и
и 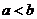 , то
, то 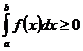
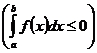 .
.
7. Если 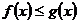 для
для 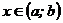 и
и 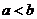 , то
, то 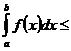
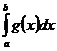 .
.
8. Если 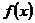 интегрируема на отрезке
интегрируема на отрезке 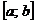 и
и 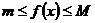 на
на 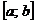 , где
, где 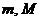 - некоторые числа, то
- некоторые числа, то  .
.
9. Если функция 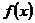 непрерывна на отрезке
непрерывна на отрезке 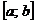 ,то существует такая точка
,то существует такая точка 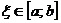 , что справедливо равенство
, что справедливо равенство 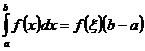 (теорема о среднем значении).
(теорема о среднем значении).






