Методические указания к выполнению:
Производной функции 
в точке 
называетсяпредел отношения приращения функции 
к приращению аргумента 
, когда приращение аргумента стремится к нулю:
или 
Обозначения производной в точке :
, 
, 
, 
или 
.
Функция , имеющая производную в каждой точке интервала 
, называется дифференцируемой в этом интервале.
Процесс отыскания производной называется дифференцированием.
Геометрический смысл производной.
Если кривая задана уравнением , то — угловой коэффициент касательной к графику функции в этой точке
Уравнение касательной к кривой в точке имеет вид: 
Правила дифференцирования
Пусть 
и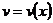 
две дифференцируемые в некотором интервале функции.
1. 
;
2. 
;
3. 
, где 
;
4. 
;
5. 
, где ;
6. 
где ;
Формулы дифференцирования основных элементарных функций
1. 
;
2. 
;
3. 
;
4. 
a > 0, a 
1;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
10. 
;
11. 
;
12. 
;
13. 
14. 
15. 
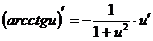
Пример 1. Найти производную функции 
.
Решение. 
.■
Пример 2. Найти производную функции 
.
Решение. 
.■
Пример 3. Найти производную функции 
.
Решение. 
.■
Правило нахождения производной сложной функции формулирует следующая теорема.
Пусть 
и 
, тогда 
-сложная функция с промежуточным аргументом и и независимым аргументом х.
Теорема. Если функция имеет производную 
в точке х, а функция имеет производную 
, в соответствующей точке , то сложная функция имеет производную 
в точке х, которая находится по формуле 
.
Пусть функция имеет в точке х отличную от нуля производную:
Если функция 
дифференцируема, то ее производная называется производной второго порядка и обозначается 
(или 
, 
; 
; 
).
Итак, 
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается 
(или 
, 
, …).
Итак, 
.
Производной n -го порядка (или n -й производной) называется производная от производной (n - 1) порядка:
Производные порядка выше первого называются производными высших порядков.
Пример 4. Найти производную функции 
Решение. Начинаем с последней операции: находим производную синуса, при этом аргумент синуса переписываем и затем умножаем на производную аргумента
.■
Пример 5. Найти производную функции 
Решение.
Пример 6. Найти производную второго порядка функции 
.
Решение. Производную второго порядка равна , поэтому найдём производную первого порядка, а затем второго.
.
.
Пример 7. Найти производную п-го порядка функции а) 
; б) 
.
а) Имеем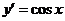 
, 
, 
, 
. Очевидно, что все последующие вычисления производных пятого, шестого и других порядков будут повторяться. Нетрудно убедиться, что производную п-го порядка можно представить в виде
, 
б) Имеем 
, 
,.... Общая формула 
. ■.
Вопросы для самоконтроля:
- Дайте понятие приращения функции.
- Сформулируйте понятие производной функции.
- Какая функция называется дифференцируемой?
- В чем состоит физический смысл производной функции?
- В чем состоит геометрический смысл производной функции?
- Дать определение касательной к кривой и записать ее уравнение.
- Какова связь между непрерывностью и дифференцируемостью функции?
- Сформулировать основные правила дифференцирования функции.
- Правило дифференцирования сложной функции.
- Что называется дифференциалом функции?
- Какова формула приближенного вычисления значения функции с помощью дифференциала?
- Что называется производной n -го порядка функции ?
