Республика Крым
Министерство образования, науки и молодежи
Государственное бюджетное профессиональное
Образовательное учреждение Республики Крым
«Симферопольский политехнический колледж»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ
по дисциплине «Математика»
19.02.03 Технология хлеба, кондитерских и макаронных изделий
15.02.01 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
РАССМОТРЕНО И ОДОБРЕНО
на заседании цикловой методической комиссии естественнонаучных и математических дисциплин
протокол №___ от «___»_________20__ г.
____________________ Ядута Н.В.
Симферополь 2018 г.
Тема: Определители 2-го и 3-го порядка.
Методические указания к выполнению:
Выражение 
называется определителем второго порядка.
Пример 1. Вычислить определитель 
.
Решение.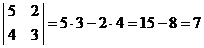 
.■
Выражение 
называется определителем третьего порядка.
Пример 2. Вычислить определитель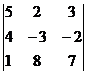 
.
Решение. 
.■
Вопросы для самоконтроля:
- Дайте определение суммы двух матриц.
- Дайте определение произведения матрицы на число.
- Дайте определение произведения двух матриц.
- Какая матрица называется транспонированной к данной?
- Что называется определителем второго порядка, третьего порядка?
- Что называется минором, алгебраическим дополнением?
- Сформулируйте основные свойства определителей.
- Сформулируйте теорему о разложении определителя по элементам строки (столбца).
- Какая матрица называется обратной квадратной матрице?
Тема: Системы линейных алгебраических уравнений. Метод Крамера решения систем линейных алгебраических уравнений.
Методические указания к выполнению:
Системами линейных алгебраических уравнений называют системы уравнений следующего вида:
Матрица 
, составленная из коэффициентов при неизвестных, называется матрицей системы:
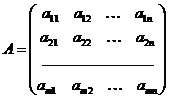
Если число уравнений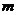 
равно числу неизвестных 
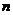, то эта матрица будет квадратной, и у нее существует определитель 
. Система может быть решена по правилу Крамера, если 
.
Правило Крамера состоит в следующем: неизвестные находятся по формулам 
, 
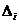равно определителю, который получается заменой в матрице 
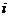- го столбца столбцом из правых частей 
системы.
Пример 1. Решить систему уравнений по формулам Крамера:
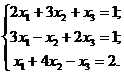
Решение.
Выпишем матрицу системы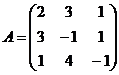 
и вычислим ее определитель
.
Значит, система имеет единственное решение. Для его нахождения вычисляем вспомогательные определители 
, заменяя в определителе 
1, 2 и 3-й столбцы столбцом свободных членов:
, 
, 
.
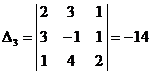По формулам Крамера будем иметь решение системы уравнений:
.■
Вопросы для самоконтроля:
- Что называется системой линейных алгебраических уравнений?
- Какая система линейных уравнений называется совместной, несовместной, определенной, неопределенной?
- Записать формулы Крамера. В каком случае они применяются?
