| Например: X= 0,1010110 Y= 0,1101000 X+Y= 1,0111110 |
При переполнении разрядной сетки, происходит перенос единицы в знаковый разряд. Это приводит к неправильному результату, причем положительное число, получившееся в результате арифметической операции может восприниматься как отрицательное (так как в знаковом разряде "1") и наоборот.
Здесь X и Y – коды положительных чисел, но ЭВМ воспринимает результат их сложения как код отрицательного числа (“1” в знаковом разряде). Для обнаружения переполнения разрядной сетки вводятся модифицированные коды.
Модифицированный обратный код – в нем под знак числа отводится не один, а два разряда. Форма записи чисел в модифицированном обратном коде выглядит следующим образом:
1) для положительного числа
X=  ; X
; X  =
=  ;
;
2) для отрицательного числа
X=  ; X
; X  =
=  ;
;
(обозначение 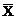 читается “не X”, т.е., если X=0, то
читается “не X”, т.е., если X=0, то 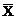 =1 и наоборот, если X=1, то
=1 и наоборот, если X=1, то 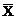 =0).
=0).
В модифицированном обратном и модифицированном дополнительном кодах под знак числа отводится не один, а два разряда: "00" соответствует знаку "+", "11" – знаку "-". Любая другая комбинация (“01” или “10”), получившаяся в знаковых разрядах служит признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем не отличается от сложения в обычных обратном и дополнительном кодах.
Рассмотрим предыдущий пример, выполнив сложение в модифицированном обратном коде:
| X= 00,101011 Y= 00,110100 X+Y= 01,011111 |
В ЭВМ в процессе работы оба знаковых разряда сравниваются. В случае появления признака переполнения машина останавливается.
Модифицированный дополнительный код также рассматривает два знаковых разряда, а во всем остальном ничем не отличается от обычного дополнительного кода, то есть:
1) для положительного числа
X=  ; X
; X 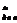 =
=  ;
;
2) для отрицательного числа
X=  ; X
; X 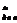 =
=  +0,000... 1;
+0,000... 1;
Пример. Даны два числа: X=101001 и Y= –11010. Сложить их в дополнительном и модифицированном дополнительном кодах.
1) Переведем X и Y в дополнительный и модифицированный дополнительный код:
| Обычная запись | Обратный код | Дополнительный код |
| X=+0101001 Y=–0011010 | Xобр=0,0101001 Yобр=1,1100101 | Xдоп=0,0101001 Yдоп=1,1100110 |
| Обычная запись | Мод. обратный код | Мод. дополнительный код |
| X=+101001 Y=–011010 | 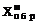 =00,101001 =00,101001
 =11,100101 =11,100101
|  =00,101001 =00,101001
 =11,100110 =11,100110
|
2) Выполним сложение:
  Xдоп= 0,0101001
Yдоп= 1,1100110
1)0,0001111
отбрасывается
(X+Y)доп= 0,0001111 Xдоп= 0,0101001
Yдоп= 1,1100110
1)0,0001111
отбрасывается
(X+Y)доп= 0,0001111
| X  = 00,101001
Y = 00,101001
Y  = 11,100110
1) 00,001111
отбрасывается
(X+Y) = 11,100110
1) 00,001111
отбрасывается
(X+Y)  = 00,001111 = 00,001111
|
Переполнения нет (в знаковых разрядах “00”), поэтому результаты, полученные в обычном и модифицированном кодах совпадают (X+Y=1111).
Упражнения 2.
1) Записать число в прямом, обратном и дополнительном кодах:
а) 11010; б) –11101; в) –101001; г) –1001110.
2) Перевести X и Y в прямой, обратный и дополнительный коды. Сложить их в обратном и дополнительном кодах. Результат перевести в прямой код. Проверить полученный результат, пользуясь правилами двоичной арифметики.
| а) X= –11010; Y= 1001111; | б) X= –11101; Y= –100110; | в) X= 1110100; Y= –101101; |
| г) X= –10110; Y= –111011; | д) X= 1111011; Y= –1001010; | е) X= –11011; Y= –10101. |
3)
Сложить X и Y в модифицированном обратном и модифицированном дополнительном восьмиразрядных кодах. В случае появления признака переполнения увеличить число разрядов в кодах и повторить суммирование. Результат перевести в прямой код и проверить, пользуясь правилами двоичной арифметики.
| а) X= 10110; Y= 110101; | б) X= 11110; Y= –111001; | в) X= –11010; Y= –100111; |
| г) X= –11001; Y= –100011; | д) X= –10101; Y= 111010; | е) X= –1101; Y= –111011. |






