При проектировании ЭВМ, создании инструментального и прикладного программного обеспечения разработчикам приходится решать вопрос о представлении в ЭВМ числовых данных. Для решения большинства прикладных задач обычно достаточно использовать целые и вещественные числа. Запись целочисленных данных в запоминающем устройстве ЭВМ не представляет затруднений: число переводится в двоичную систему и записывается в прямом коде. Диапазон представляемых чисел в этом случае ограничивается количеством выделенных для записи разрядов. Для вещественных данных обычно используются две формы записи: число с фиксированной точкой (ЧФТ) и число с плавающей точкой (ЧПТ).
Числа с фиксированной точкой.
Форма записи числа с фиксированной точкой использовалась в основном на ранних этапах развития вычислительной техники. Запись числа с фиксированной точкой обычно имеет знаковый и цифровой разряды. Фиксированная точка означает, что на этапе конструирования ЭВМ было определено, сколько и какие разряды машинного слова отведены под изображение целой и дробной частей числа. Запятая в разрядной сетке может быть зафиксирована, в принципе, после любого разряда.
Пример.
Ячейка с целой и дробной частью.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

| 
| 
| 
| 
| 
| 
|
|
Знак Целая часть Дробная часть числа (n разрядов) (m разрядов) |
Как частный случай числа с фиксированной точкой, может быть рассмотрена запись целого числа (в этом случае все разряды, кроме знакового, используются для записи целой части).
Ячейка с записью целого числа.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

| 
| 
| 
|
|
Знак Цифровые разряды (n) числа |
К достоинствам использования чисел с фиксированной точкой относятся простота выполнения арифметических операций и высокая точность изображения чисел. К недостаткам – небольшой диапазон представления чисел.
Числа с плавающей точкой.
Для представления чисел с плавающей точкой (ЧПТ) используется полулогарифмическая форма записи числа:

где 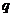 – основание системы счисления,
– основание системы счисления,  – порядок числа,
– порядок числа,  – мантисса числа
– мантисса числа  .
.
Положение точки определяется значением порядка  . С изменением порядка точка перемещается (плавает) влево или вправо.
. С изменением порядка точка перемещается (плавает) влево или вправо.
Пример.

Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа может изменяться в диапазоне: 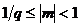 . Таким образом, в нормализованных числах цифра после точки должна быть значащей.
. Таким образом, в нормализованных числах цифра после точки должна быть значащей.
Пример.

ненормализованное нормализованное
число число
Для представления чисел в машинном слове выделяют группы разрядов для изображения мантиссы, порядка, знака числа и знака порядка:
а) представление чисел в формате полуслова
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
 
|

Знак Знак Порядок p Мантисса m

 (4 разряда) (10 разрядов)
(4 разряда) (10 разрядов)
| б) представление чисел в формате слова
Знак Знак Порядок p Мантисса m
| ||||||||||||||||||||||||||||||||
Наиболее типично представление ЧПТ в формате слова (32 разряда).
Пример.
а) Число А  записывается в ячейку следующим образом:
записывается в ячейку следующим образом:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 31 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | ... | 0 | ||||
|
Знак Знак Порядок p Мантисса m
|
б)Число А 
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 31 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | ... | 0 | ||
|
Знак Знак Порядок p Мантисса m
|
Максимальным числом представимым в формате слова будет
А 

.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 31 | ||
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ... | 1 | ||
|
Зн |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 31 | ||
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ... | 1 | ||
|
Зн |
Минимальным числом из возможно представимых в формате слова будет А 

Минимальным по модулю, отличным от нуля и нормализованным будет А  .
.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 31 | ||
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | ... | 0 | ||
|
Зн |
| 0 | 1 | 2 | 3 | 11 | 12 | 13 | 31 | 0 | 1 | 31 | |||||
 
| ... | ... | ... | ||||||||||||
| Знак Знак Порядок p Мантисса m
|
Таким образом, числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения чисел определяется только разрядами мантиссы и уменьшается по сравнению с числами с фиксированной точкой. При записи числа в формате слова диапазон представимых чисел будет от  до
до 
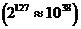 , а точность определяться мантиссой, состоящей из 23 разрядов. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):
, а точность определяться мантиссой, состоящей из 23 разрядов. Точность может быть повышена путем увеличения количества разрядов мантиссы. Это реализуется путем представления чисел с так называемой двойной точностью (используется формат двойного слова):
Литература.
1. Пономарев В.С., Красников В.В. Методические указания по курсу "Организация и функционирование ЭВМ и систем". Ч. 1. Арифметические основы ЭВМ. ДГТУ, 1996.
2. Каган Б.М. Электронные вычислительные машины и системы. М.: Энергоатомиздат, 1991.
3. Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высшая школа, 1983.
4. Лю Ю-Чжен, Гибсон Г. Микропроцессоры семейства 8086/8088. М.: Радио и связь
* Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы к которой относится число будем указывать в виде нижнего индекса.
* Знаковым разрядом обычно является крайний разряд в разрядной сетке. В дальнейшем при записи кода знаковый разряд от цифровых условимся отделять запятой. Если количество разрядов кода не указано будем предполагать, что под запись кода выделен один байт.