Любая информация (числа, команды, записи и т. п.) представляется в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют разрядами или битами. Двоичный код состоящий из 8 разрядов носит название байта. Для записи чисел также используют 32-разрядный формат (машинное слово), 16-разрядный формат (полуслово) и 64-разрядный формат (двойное слово).
Коды чисел.
В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ, а также при умножении и делении. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ. К кодам выдвигаются следующие требования:
1) Разряды числа в коде жестко связаны с определенной разрядной сеткой.
2) Для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд. Например, если за основу представления кода взят один байт, то для представления числа будет отведено 7 разрядов, а для записи кода знака один разряд.
Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.*
Пример. В случае, когда для записи кода выделен один байт, для числа +1101 прямой код 0,0001101, для числа –1101 прямой код 1,0001101.
Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Пример.
Для числа +1101 прямой код 0, 0001101; обратный код 0,0001101.
Для числа –1101 прямой код 1, 0001101; обратный код 1,1110010.
Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
Пример.
Для числа +1101:
прямой код обратный код дополнительный код
0,0001101 0,0001101 0,0001101
Для числа –1101:
прямой код обратный код дополнительный код
1,0001101 1,1110010 1,1110011
Особенности сложения чисел в обратном и дополнительном кодах.
При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается.
При сложении чисел в обратном коде возникающаяединица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.
Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах, кроме знакового, на противоположные. Дополнительный код преобразуется в прямой так же, как и обратный, с последующим прибавлением единицы к младшему разряду.
Пример.
Сложить X и Y в обратном и дополнительном кодах.
а) X= 111, Y= –11;
1) Сложим числа, пользуясь правилами двоичной арифметики:
| X= 111 Y= – 11 X+Y= 100 |
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополни-тельном коде |
 Xпр=0,0000111
Yпр=1,0000011
| Xобр= 0,0000111
Yобр= 1,1111100
1 0,0000011
  +1
(X+Y)обр= 0,0000100
| Xдоп= 0,0000111 Yдоп= 1,1111101 10,0000100 отбрасывается (X+Y)доп= 0,0000100 |
Так как результат сложения является кодом положительного числа (знак 0), то (X+Y)обр=(X+Y)доп=(X+Y)пр .
б) X= –101,Y= –11;
1) Сложим числа, пользуясь правилами двоичной арифметики:
| X= – 101 Y= – 110 X+Y= –1011 |
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополни-тельном коде |
 Xпр=1,0000101
Yпр=1,0000110
| Xобр= 1,1111010 Yобр= 1,1111001 1 1,1110011 +1 (X+Y)обр= 1,1110100 | Xдоп= 1,1111011 Yдоп= 1,1111010 1)1,1110101 отбрасывается (X+Y)доп= 1,1110101 |
Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код:
а) из обратного кода
(X+Y)обр=1,1110100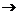 
(X+Y)пр=1,0001011;
б) из дополнительного кода
(X+Y)доп=1,1110101 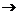(X+Y)пр=1,0001010+0,0000001=1,0001011.
Таким образом, X+Y= –1011 и полученный результат совпадает с обычной записью
