Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Пример.
а) Перевести  с.с. *
с.с. *



б) Перевести  с.с.
с.с.

в) Перевести  с.с.
с.с.
 .
.
Перевод целых десятичных чисел в восьмеричную, шестнадцатеричную и двоичную системы осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример.
а) Перевести  с.с.
с.с.
| 181 | 8 | |
| 176 | 22 | 8 |
| 5 | 16 | 2 |
  
|  6 6
|
Результат  .
.
б) Перевести  с.с.
с.с.
| 622 | 16 | |
| 48 | 38 | 16 |
| 142 | 32 | 2 |
| 128 |  6 6
| |
  14 14
|
Результат 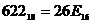 .
.
Перевод правильных дробей из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести  с.с.
с.с.
| 0 | 3125 ´ 8 |
| 2 | 5000 ´ 8 |
| 4 | 0000 |

Результат  .
.
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести  с.с. Точность 6 знаков.
с.с. Точность 6 знаков.
| 0 | 65´ 2 | |
| 1 | 3 ´ 2 | |
| 0 | 6 ´ 2 | |
| 1 | 2 ´ 2 | |
| 0 | 4 ´ 2 | |
| 0 | 8 ´ 2 | |
| 1 | 6 ´ 2 | |
...





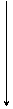
 .
. с.с.
с.с.

 2
2

 ;
; 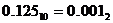 . Результат:
. Результат:  .
.
 =
=  ;
; 
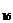 =
=  .
. с.с.
с.с.

 с.с.
с.с.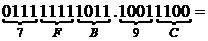

 с.с.
с.с.

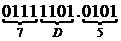


 .
. 1 1
1 1



 ; б)
; б)  ; в)
; в) 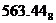 ; г)
; г)  ; д)
; д) 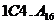 ; е)
; е)  .
.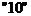 с.с в
с.с в  с.с.:
с.с.: ; б)
; б)  ; в)
; в) 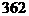 ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;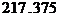 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г) 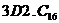 .
.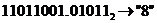 с.с.;
с.с.;  с.с.;
с.с.; с.с.; г)
с.с.; г) 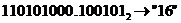 с.с..
с.с..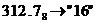 с.с.; б)
с.с.; б) 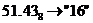 с.с.;
с.с.; с.с.; г)
с.с.; г)  с.с..
с.с.. , Y=
, Y=  ;
; , Y=
, Y=  ;
; , Y=
, Y=  .
. , Y=
, Y= 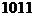 ;
; , Y=
, Y=  ;
; , Y=
, Y=  ;
; , Y=
, Y=  .
.
