В качестве экспериментальной установки (рисунок 1) в данной лабораторной работе используется крестообразный маховик, приводящийся во вращательное движение падающим грузом (1). Маховик состоит из двух шкивов с радиусами R1 и R2 (2) и четырех стержней (3), укрепленных на шкивах под прямым углом друг к другу. Момент инерции маховика можно изменять, перемещая на стержнях грузы одинаковой массы (4) на определенное расстояние от оси вращения. Момент силы, вызывающий вращение маховика, создается силой натяжения нити (Fн), намотанной на один из шкивов, к которой привязан груз (1). Момент силы можно изменять, подвешивая грузы разной массы, или изменяя плечо силы, наматывая нить на шкивы разного радиуса (R1 или R2).
Рисунок 1 – Крестообразный маховик
Расчетные формулы
Силу натяжения нити во время несвободного равноускоренного падения груза с высоты h вычислим по второму закону Ньютона
к 
Момент силы (М)
M = Fн · R = m (g – αк) · R (8)
Угловое ускорение (ε) выразим через линейное ускорение (а к) точки подвеса груза (1) к маховику по известной формуле связи
ак = ε · R 
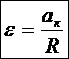(9)
Линейное ускорение точки подвеса груза равно линейному ускорению самого груза, который совершает равноускоренное падение с высоты h из состояния покоя (υ0=0).
(10)
Экспериментальная часть
Задание. Установить характер зависимости углового ускорения от мо-
мента силы.
1 Измерить штангенциркулем диаметр малого и большого шкива, рассчитать радиусы этих шкивов в метрах и записать их в таблицу.
2 Подвесить на нить груз массой 0,5 кг и намотать нить на шкив малого радиуса до высоты груза над поверхностью пола h = 1,2 м.
3 Измерить время падения груза с этой высоты 3 раза. Секундомер включать в момент начала движения груза и выключать в момент удара его о поверхность пола. Среднее время записать в таблицу.
4 Намотать нить на шкив большого радиуса и измерить время падения груза с той же высоты 3 раза.
5 Подвесить на нить груз массой 0,7 кг и измерить время падения груза при малом и большом радиусе шкива.
6 По формулам 8, 9, 10 вычислить ак, ε и М, используя среднее время падения. Результаты записать в таблицу.
7 По полученным экспериментальным данным построить график зависимости ε от М. Сделать вывод о характере этой зависимости.
8 Используя график, вычислить момент инерции маховика по формуле (11)
(11)
Таблица 2 – Результаты измерений
| № | m | R·10-3 | tср | ак | ε | М | I |
| кг | м | с | м/с2 | рад/с2 | Н·м | кг·м2 | |
| 1 | 0,5 | R1= | |||||
| 2 | 0,5 | R2= | |||||
| 3 | 0,7 | R1= | |||||
| 4 | 0,7 | R2= |
Вопросы для допуска к работе
1 Сформулировать основную цель лабораторной работы.
2 Сформулировать основной закон динамики вращательного движения.
3 Знать расчетные формулы для вычисления М, ак и ε.
Вопросы для зачета по работе
1 Дать определение кинематических и динамических физических вели-
чин, применяемых для описания вращательного движения.
2 Сделать вывод уравнения (закона) динамики вращательного движения
твердого тела.
Литература
Трофимова Т. И. Курс физики: учеб. пособие для вузов. – 18-е изд., сте-
реотип. – М.: Академия, 2010. – 560 с.
ЛАБОРАТОРНАЯ РАБОТА № 2
ИССЛЕДОВАНИЕ СВОБОДНЫХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ
ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы
1 Изучить теорию свободных гармонических колебаний маятников. 2 Экспериментально исследовать затухающие колебания физического маятника.
Теоретическое введение
В этой лабораторной работе изучаются свободные затухающие гармонические колебания физическое маятника.
Физическое явление гармонические колебания – это периодические изменения состояние системы при котором различные параметры системы изменяются по закону синуса или косинуса.
Свободные колебания – это колебания, происходящие только под действием внутренней квазиупругой силы.
Затухающие колебания – это колебания при наличии, кроме внутренней возвращающей силы, внешней силы трения.
Физический маятник – это любое твёрдое тело, совершающее колебания вокруг закреплённой горизонтальной оси подвеса (о), не проходящей через центр масс (с) тела (рисунок 2).
Одним из основных параметров, определяющих состояние механически колеблющейся системы (маятника), является смещение (х) любой точки этой системы относительно своего положения равновесия.
При действии на систему только одной внутренней возвращающей силы смешение изменяется по гармоническому закону:
(12)
Здесь А – амплитуда колебания, равная максимальному смещению
(А = Xmax).
(ωot + φo) – фаза колебания
ωo – циклическая частота собственных колебаний;
,
где φо – начальная фаза колебания;
То – период собственных колебаний, т. е. время одного колебания;
no - частота собственных колебаний, т. е. число колебаний за единицу времени.
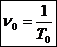
При действии на систему (маятник) силы трения (кроме внутренней возвращающей силы) амплитуды колебания будут уменьшаться с течением времени. Такие колебания называются затухающими. Уравнение затухающих колебаний имеет следующий вид:
, (13)
где Ао – начальная амплитуда при t = 0;
δ – коэффициент затухания;
- циклическая частота затухающих колебаний;
- амплитуда затухающих колебаний в любой момент времени.
Графическое изображение уравнения затухающих колебаний приведено на рисунке 1.
Количественно быстрота уменьшения амплитуды за один период колебания характеризуется декрементом затухания (d) и логарифмическим декрементом (q):
(14)
q = 
Рисунок 2 – График затухающих колебаний
