Идея экспериментального исследования

МЕХАНИКА И МОЛЕКУЛЯРНАЯ ФИЗИКА

Методические указания

по выполнению лабораторных работ

для студентов инженерного факультета

Курган - 2013

УДК 53 (075.8)

А 48

Аленькин В. И., Корнева Т. С. Механика и молекулярная физика: методические указания по выполнению лабораторных работ для студентов инженерного факультета.

- Курган: издательство КГСХА, 2013 – 39 стр.

Рецензент: кандидат физико-математических наук, доцент Московченко Г. А.

Методические указания подготовлены в соответствии с государственным образовательным стандартом и программой курса физики по направлению подготовки 110800 – Агроинженерия. Изложено содержание лабораторных работ и порядок их выполнения.

Методические указания рассмотрены и одобрены на заседании кафедры физики (протокол №1 от 26.09.2012), утверждены и рекомендованы к изданию методической комиссией инжененрного факультета (протокол №2 от 27.10.2012)

сельскохозяйственная академия имени

Т.С. Мальцева», 2013

ВВЕДЕНИЕ. ОРГАНИЗАЦИЯ РАБОТЫ СТУДЕНТА
В ФИЗИЧЕСКОМ ПРАКТИКУМЕ

Лабораторные работы практикума разбиты на несколько циклов, которые выполняются по мере ознакомления студентов с теорией явлений на лекциях. Студентам предварительно сообщаются номера работ, которые они будут выполнять в данном цикле и последовательность их выполнения. Выполнение лабораторной работы практикума состоит из трех этапов.

Первый этап выполняется до занятия и состоит в большой предварительной подготовке к проведению физического эксперимента и к зачету по лабораторной работе цикла. Так как время студента в течение занятия крайне ограничено, то предварительная подготовка значительно упрощает его работу. Она заключается в изучении теории тех явлений, которые исследуются в лабораторной работе, с последующими ответами на контрольные вопросы, помещенные в конце описания каждой работы; в предварительном составлении письменного отчета со следующим порядком записей: название и номер работы, расчетные формулы с пояснением обозначений физических величин, таблицы для записей результатов измерений; в изучении порядка выполнения работы, задачи и целей эксперимента, иными словами, студент должен четко представлять себе, что и как делать при выполнении работы. Без предварительной подготовки студент не допускается к выполнению эксперимента.

Вторым этапом является проведение физического эксперимента в лаборатории в течение занятия. При работе в лаборатории необходимо помнить следующее. До начала выполнения эксперимента следует ознакомиться с принадлежностями и оборудованием, необходимым для работы. Нельзя брать принадлежности с другого лабораторного стола. Работу следует начинать только с разрешения преподавателя после беседы о допуске к работе, измерения проводить тщательно. После проведения эксперимента необходимо тут же, в лаборатории, подсчитать окончательный результат измерений и дать его на контроль преподавателю. В случае неудовлетворительного результата, необходимо измерения провести снова. Правильно выполненная работа должна быть подписана преподавателем. Без такой подписи работа зачету не подлежит.

Третий этап работы состоит в сдаче преподавателю зачета по выполненной работе, при этом предъявляется законченный письменный отчет, в котором кроме данных предварительной подготовки приведены как первичные результаты эксперимента, так и окончательная обработка результатов эксперимента. Зачет по работе предполагает ответ на те контрольные вопросы, которые поставит преподаватель (ответы на эти вопросы студент должен подобрать в процессе предварительной подготовки к занятию).

ВВОДНАЯ ЛАБОРАТОРНАЯ РАБОТА

РАСЧЕТ ОШИБОК ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН

Цель работы: изучить краткую теорию расчета погрешностей измере-

ний физических величин.

Теоретическое введение

1 Виды измерений

При проведении экспериментального исследования различают прямые и косвенные измерения физических величин.

Прямые измерения – это такие измерения, которые производятся измерительными приборами непосредственно.

В тех случаях, когда измерение данной физической величины с помощью какого - либо прибора невозможно, производится вычисление этой величины, с использованием результатов прямых измерений других величин, с которыми она связана. Такие вычисления и называются косвенными измерениями. Например, требуется измерить площадь (Ѕ) прямоугольной фигуры. Для этого измеряют длину (а) и ширину (в) этой фигуры и вычисляют площадь по формуле Ѕ = а · в. Здесь значение Ѕ – косвенное измерение.

Когда требуется знать значение величины более точно, применяют многократные измерения.

2 Виды погрешностей измерений

Поскольку приборы и наши органы чувств несовершенны, а также по целому ряду других причин, в результате измерений всегда содержатся погрешности (ошибки), т.е. нет абсолютно точных измерений.

Погрешности измерений делятся на три класса:

1) систематические погрешности – это ошибки, которые появляются систематически, поэтому причины их известны и могут быть выявлены. Влияние этого рода погрешностей на результат измерения можно учесть введением поправки и тем самым исключить эту погрешность;

2) грубые погрешности (промахи) – это большие ошибки, возникающие по различным причинам, либо в результате невнимательности или из-за неправильного способа измерений, или в результате неумения пользоваться прибором. Измерения, содержащие этот тип погрешностей, отбрасываются как неверные и в дальнейшем не используются. Как это делается – разъясняется и показывается ниже.

3) случайные погрешности – это ошибки, возникающие по различным случайным причинам, поэтому предупредить появление этого типа ошибок нельзя. Случайные погрешности оказывают определенное влияние на точность измерений. Однако при многократных измерениях они подчиняются статистическим законам, и их влияние на результаты измерений можно уменьшить. Таким образом, если систематические и грубые погрешности можно исключить из результатов измерений полностью, то для случайных погрешностей это не представляется возможным. Поэтому в дальнейшем будет идти речь об учете только случайных погрешностей.

Случайные погрешности подразделяются на абсолютные и относительные ошибки.

Абсолютная погрешность (Δx) – это отклонение результата измерения некоторой величины (x _изм) от истинного значения этой величины (x)

Δx = x - x _изм (1)

Оценить точность измерения позволяет относительная погрешность (ε_x), которая показывает, какую долю абсолютная погрешность составляет от истинного значения измеряемой величины

ε_x = (2)

3 Расчет погрешностей при прямых многократных измерениях

При многократных измерениях некоторой физической величины (x) было получено n значений: (x_1, x₂, … x_n). Так как случайные погрешности с равной вероятностью приводят как к завышению, так и к занижению результатов измерения по сравнению с истинным значением величины x, то за наиболее близкое к истинному значению принято считать среднее (x_ср) арифметическое всех проведенных измерений:

x_ср = (3)

Абсолютная погрешность каждого измерения (Δx_i) рассчитывается по формуле

Δx_i = x_i - x_ср (4)

Для оценки точности каждого измерения рассчитывается стандартное отклонение от среднего (Δx_ст)

Δx_ст = (5)

Если абсолютная ошибка какого-либо измерения (Δx_i) превышает 3Δx_ст., т. е. Δx_i > 3Δx_ст, то соответствующее измерение содержит грубую погрешность, и его исключают из дальнейших расчетов. Из теории вероятности следует, что предельная (средняя) погрешность измерения физической величины (Δx_ср) рассчитывается по формуле:

Δx_ср = , (6)

где Δx_ст – стандартное отклонение от среднего;

n – количество измерений.

Относительная погрешность прямого измерения измеряемой величины рассчитывается по формуле:

ε_x = . (7)

4 Расчет погрешностей косвенных измерений физической величины

В качестве косвенно измеряемой величины рассмотрим площадь (Ѕ) прямоугольника со сторонами а и в. Площадь рассчитывается по формуле:

Ѕ = а · в (8)

Так как при прямых измерениях величин а и в получаются погрешности Δа_ср и Δв_ср, то и площадь Ѕ тоже будет вычислена с определенной погрешностью Δ Ѕ_ср. Зная средние значения а_ср, в_ср, Δа_ср, Δв_ср, можно рассчитать погрешность Δ Ѕ_ср, применяя дифференциальный метод. Суть этого метода заключается в следующем:

1 косвенно измеряемая величина (Ѕ) является функцией прямоизме-

ряемых величин

Ѕ = F_(а,в) = а · в (9)

2 вычислим полный дифференциал (dF)этой функции, равный сумме

частных дифференциалов по каждой переменной

dF_(а,в) = f ′_(а)dа + f ′_(в)dв dS_(а,в) = в·dа + аdв (10)

3 заменим значок d на Δ и присвоим всем величинам средние

значения

ΔЅ_ср = в_ср Δа_ср + а_ср Δв_ср (11)

Полученное выражение является средней абсолютной погрешностью косвенно-измеряемой величины

4 относительная погрешность косвенно-измеряемой величины равна

ε_S = , (12)

где Ѕ_ср = а_ср · в_ср (13)

Экспериментальная часть

Задание. Измерить площадь прямоугольника и рассчитать ошибки измере-

ния площади.

Порядок выполнения эксперимента

1 Штангенциркулем измерить длину (а_i) и ширину (в_i) прямоугольника несколько раз (n).

2 Рассчитать средние значения измеренных величин (а_ср) и (в_ср) по формуле (3).

3 Рассчитать абсолютные погрешности каждого измерения (Δа_i) и (Δв_i) по формуле (4).

4 Рассчитать стандартные отклонения (Δа_ст и Δв_ст) по формуле (5).

5 Исключить грубые погрешности каждого измерения а и в.

6 Рассчитать предельные (средние) погрешности Δа_ср и Δв_ср по формуле (6).

7 По формуле (13) рассчитать среднее значение площади (Ѕ_ср).

8 По формуле (10) рассчитать среднюю абсолютную погрешность площади (ΔЅ_ср).

9 По формуле (12) рассчитать относительную погрешность площади в процентах (ε_S).

10 Записать конечный результат измерения площади в виде

Ѕ = Ѕ_ср ΔЅ_ср.

11 Результаты измерений и расчетов занести в таблицу 1.

Таблица 1 - Результаты измерений

№	а_i	Δа_i	в_i	Δв_i	Ѕ_ср	ΔЅ_ср	ε_S
№	мм	мм	мм	мм	мм²	мм²	%
1
2
3
4
среднее

Окончательный результат записать в виде

Ѕ = (Ѕ_ср ΔЅ_ср) мм².

Вопросы для зачета

1 Понятие абсолютной и относительной погрешности измерений физической величины.

2 Как исключаются грубые погрешности измерений.

3 Суть дифференциального метода расчета погрешностей измерения косвенной величины.

ЛАБОРАТОРНАЯ РАБОТА № 1

ИЗУЧЕНИЕ ЗАКОНОМЕРНОСТЕЙ ВРАЩАТЕЛЬНОГО

ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Цели работы

1 Изучить основные кинематические и динамические физические величины,

применяемые для описания вращательного движения.

2 Экспериментально установить зависимость углового ускорения от момента силы, действующей на тело с закрепленной осью вращения.

Теоретическое введение

Для описания вращательного движения введены специальные кинематические и динамические величины.

Кинематические характеристики вращательного движения называются угловыми:

Угловое перемещение - векторная величина, численно равная углу поворота радиуса, соединяющего точку с осью вращения (радиан).

Угловая скорость - векторная величина, численно равная изменению углового перемещения за единицу времени (рад/с)

(1)

Угловое ускорение - векторная величина, численно равная изменению угловой скорости за единицу времени (рад/с²).

(2)

Вектора всех угловых физических величин направлены по оси вращения (правило буравчика).

Динамические характеристики вращательного движения:

Момент силы (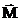) – векторная величина, численно равная произведению модуля силы (F) на плечо силы (d) (Н·м)

(3)

Момент инерции тела (I) – скалярная величина, численно равная сумме моментов инерции всех материальных точек тела I_i (кг · м²):

(4)

Момент импульса тела - векторная величина, численно равная произведению момента инерции тела на угловую скорость:

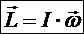(5)

Динамические и кинематические характеристики движения связаны между собой основным законом (уравнением) динамики вращательного движения:

(6)

Вектора 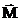и направлены по оси вращения.

Идея экспериментального исследования

Основной целью в данной лабораторной работе является экспериментальная проверка закона динамики вращательного движения, в частности, зависимости углового ускорения вращающегося тела от действующего на него момента силы.

Из основного закона динамики вращательного движения (6) следует, что угловое ускорение зависит прямо пропорционально от момента силы: М~I и обратно пропорционально - от момента инерции тела (ε ~ )

(7)

Для экспериментальной проверки зависимости ε от М при I = const на вращающееся тело с закрепленной осью вращения (рис.1) поочередно действуют различные моменты силы, и при каждом моменте силы определяется угловое ускорение вращающегося тела.

Итогом этого эксперимента является построение графика зависимости ε от М, из которого выясняется как ε зависит от М.