Цель работы: экспериментальное исследование переходных процессов в линейных неразветвленных электрических цепях с од- ним и двумя накопителями энергии.
32
Общие сведения
Переходные процессы возникают в цепях, содержащих ин- дуктивные катушки и конденсаторы, так как эти элементы обла- дают способностью накапливать и отдавать энергию соответст- венно магнитного и электрического полей. Возникновение пере- ходных процессов объясняется тем, что индуктивные катушки и конденсаторы являются инерционными элементами, то есть из- менение электрического и магнитного полей не может происхо- дить мгновенно. Расчет напряжений и токов на участках иссл е- дуемой электрической цепи во время переходного процесса про- изводят, пользуясь линейными дифференциальными уравнения- ми, составленными в соответствии с законами Кирхгофа для мгновенных значений токов и напряжений. Определение токов и напряжений переходного режима сводится к интегрированию системы линейных дифференциальных уравнений. Решение л и- нейного дифференциального уравнения складывается из частно- го решения неоднородного уравнения и общего решения одно- родного уравнения:
| i i пр i св; u u пр u св , | (7.1) |
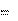где
i пр, u пр
принужденные токи и напряжения, полученные в ре-
зультате частного решения;
i св, u св
свободные токи и напряже-
ния, полученные в результате решения однородного дифференци- ального уравнения.
Рассмотрим переходные процессы в электрической цепи при заряде конденсатора C от источника постоянной ЭДС E через ре-
зистор
R 1 (рис. 7.1, а – ключ K в положении 1) и при разряде кон-
денсатора C на резистор R 2
(рис. 7.1, а – ключ K в положении 2).
При замыкании ключа в положении 1 конденсатор C будет заря- жаться до тех пор, пока напряжение нем не станет равно напряжению
источника питания. Переходное напряжение на конденсаторе u c
дет изменяться по возрастающей экспоненте (рис. 7.1, б):
бу-
33
| t u c E (1 e 1), | (7.2) |
где 1
R 1 C
постоянная времени процесса заряда.
Переходный зарядный ток тоже изменяется по экспоненциаль- ному закону (рис. 7.1, б):
| du E t
i C C e ,
dt R
| (7.3) |
Переходный процесс возникает и при разряде заряженного до напряжения E конденсатора C через последовательно включен-
ное сопротивление
R 2. При замыкании ключа K в положение 2
(рис. 7.1, а) переходные напряжения u c
и ток i уменьшаются,
асимптотически приближаясь к нулю, при этом переходное напря- жения на конденсаторе
| t
u c E e 2,
| (7.4) |
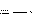
а переходный ток
| t i E e 2. R | (7.5) |
Графики изменения тока и напряжения на конденсаторе пред- ставлены на рис. 7.1, в. При разряде конденсатора запасенная в нем энергия электрического поля преобразуется в тепло, которое выде-
ляется в сопротивлении
R 2. Длительность переходного процесса
при разряде конденсатора зависит от постоянной времени
2 R 2 C.
Включение в цепь разряда конденсатора катушки индуктивно- сти L (рис. 7.2, а), то есть еще одного реактивного элемента, при- водит к увеличению степени дифференциального уравнения, опи- сывающего переходные процессы в контуре:
| d 2 i R di 1 i 0, dt 2 L dt LC | (7.6) |
где R R 2 R L.
34
|
| |
| а | |
|
|
| б | в |
| Рис. 7.1 | |
Дифференциальному уравнению (7.6) соответствует характери- стическое уравнение:
p 2  R  p 1 0.
L LC
| (7.7) |
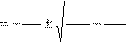Если корни этого уравнения
| R R 2 1 p 1,2 2 L 4 L 2 LC | (7.8) |
являются разными вещественными числами, что имеет место при соблюдении неравенства
| R 2 L, C | (7.9) |
то переходный ток разряда конденсатора определяется выражением
| i Cp 1 p 2 U 0 (e p 1 t e p 2 t ), p 2 p 1 | (7.10) |
35
а переходное напряжение на зажимах конденсатора – формулой
| u U 0 (p e p 1 t p e p 2 t), c p p 2 1 2 1 | (7.11) |
где напряжение U 0
u c (0
определяется начальными условиями.
При этом, как видно из выражений (7.10) и (7.11), величины i и
u c в течение переходного процесса сохраняют неизменное направ-
ление и заряд конденсатора будет апериодическим (рис. 7.2, б).
|
| |
| а | |
|
|
| б | в |
| Рис. 7.2 | |
Аналогичные переходные процессы имеют место при равных
корнях
p 1, p 2
характеристического уравнения (7.7), когда значе-
ние сопротивления R, называемого критическим, определяется формулой
| R 2 L. кр C | (7.12) |
Если параметры R, L, C таковы, что
| R 2 L, C | (7.13) |
36
корни характеристического уравнения (7.7) будут комплексными и сопряженными:
| p 1,2 j 0, | (7.14) |
где
| 1 R 2 0 LC 4 L 2, | (7.15) |
| R. 2 L | (7.16) |
В этом случае в цепи будет наблюдаться затухающий колеба- тельный переходный процесс (рис. 7.2, в) с угловой частотой собст- венных колебаний 0, при котором переходный ток и переходное напряжение на зажимах конденсатора определяется выражениями:
| i U 0 e t sin(t ), L 0 0 | (7.17) |
| u U 0 e t sin(t ). c LC 0 0 | (7.18) |
Программа работы
1. Определить параметры схем замещения реактивных элемен- тов: конденсатора С и катушки индуктивности L с внутренними
сопротивлениями R C
подавателя).
и R L
соответственно (согласно заданию пре-
2. Собрать схему рис. 7.1, а, подключить осциллограф к обклад- кам конденсатора.
3. Получить на экране неподвижное изображение процессов за- ряда-разряда конденсатора по схеме рис. 7.1, а с одним накопителем энергии. Проделать опыт для трех различных значений сопротивле-
ний
R 1 и
R 2. Скопировать осциллограммы переходных процессов.
Записать параметры схем.
4. Собрать схему рис. 7.2, а, подключить осциллограф к обклад- кам конденсатора.
37
5. Исследовать переходные процессы в электрической цепи с двумя накопителями энергии, проведя три опыта при различных со- отношениях параметров схемы.
5.1. R 2 R L R C
5.2. R 2 R L R C
5.3. R 2 R L R C
2 L.
C
2 L.
C
2 L.
C
Скопировать осциллограммы переходных напряжений на об- кладках конденсатора и записать параметры схем, при которых эти осциллограммы были получены.
6. 
По результатам опытов пункта 3 вычислить значения посто- янных времени 1 и 2 для проведенных опытов.
7. По осциллограмме для колебательного процесса (п. 5.3) опре-
делить период и частоту собственных колебаний и сравнить их со значениями, полученных из соотношения (7.15) по известным пара- метрам схемы.
8. 
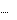
Из соотношения (7.15’) определить индуктивность катушки по данным опыта согласно п. 5.3 и сравнить с результатом, полу- ченным в п. 1:
4  16 16 R 2 C 2 2 L 0. 1,2 8 C 2
0
| (7.15’) |
Сод ер жание о тчета:
− схемы рис. 7.1, а, 7.2, а;
− осциллограммы проведенных опытов;
− расчеты согласно п.п. 6 8;
− выводы.
Контрол ь ные вопр о сы и зад ания
1. Объясните физическое содержание и физические причины переходных процессов.
38
2. Какие соотношения существуют между переходными и сво- бодными токами и напряжениями?
3. Как формулируются законы коммутации?
4. Что называют постоянной времени электрической цепи? Ка- ков ее физический смысл?
5. Каково влияние параметров электрических цепей на характер и продолжительность переходного процесса?
6. Куда расходуется энергия при разряде конденсатора?
7. Какие условия должны быть соблюдены для апериодического и колебательного разрядов конденсатора?
8. От чего зависит период колебаний тока при разряде конден- сатора?
9. Какую опасность представляет собой размыкание цепей, со- держащих катушки с большой индуктивностью?
10. Почему конденсатор сравнительно большой емкости после его отключения от источника питания представляет опасность для жизни человека?
Л аборатор ная ра бот а № 8
