Для различных центров приведения получим всегда одну и туже силу, но пары будут разными.
Следствие.
Две системы сил будут эквивалентными, если у них будут одинаковые характеристические величины, построенные в той же точке тела.
Из данной теоремы следует, что если хоть одна из характеристических величин системы отлична от нуля, то система будет неуравновешенной.
Аналитический метод определения характеристических величин системы сил.
Пусть к нему приложены силы  ,
,  ,…,
,…, 
Пусть известны проекции силы 
 {XK,YK,ZK}
{XK,YK,ZK}
и координаты точки приложения сил АК
АК = {XK,YK,ZK }
где
(к= 1,2,….,. n)
Требуется определить по модулю и направлению  и
и  .
.
Вспомним:
 =
= 
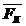
Спроецируем это векторное равенство на оси координат:
 |
Затем можем найти модуль главного вектора по его проекциям с помощью теоремы Пифагора
Откуда:
 |
Направление этого вектора определим с помощь направляющих модулей:
с os ( *,
*,  ) =
) = 
с os ( *,
*,  ) =
) = 
с os ( *,
*,  ) =
) = 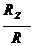
Задача полностью решена для главного момента.
По определению:
 =
= 
 (
( )
)
Спроецируем на координатные оси и получим (проекции главного момента на оси координат равны проекциям векторного момента сил относительно точки О на координатных осях):
М О X =  m О X (
m О X ( )
)
M О Y =  m О Y (
m О Y ( )
)
M О Z =  m О Z (
m О Z ( )
)
Как известно моменты сил относительно точки и оси:
moX( ) =mX(
) =mX( ) и т.д.
) и т.д.
Тогда
М О X =  mX(
mX( )
)
M ОY=  mY(
mY( )
)
M О Z =  mZ (
mZ ( )
)
Эти суммы являются главными моментами относительно координатных осей.
Таким образом,
М О X = М X
M О Y = M Y
M О Z = M Z
Модуль главного момента относительно точки О вычисляется также по теореме Пифагора:
МО= 
Осталось определить направляющие косинусы:
с os (  ,
,  ) =
) = 
с os (  ,
,  ) =
) = 
с os (  ,
,  ) =
) = 
Приведение системы сил к простейшему виду.
Приведение системы сил к равнодействующей.
Формулировка теоремы:
Если для произвольного центра приведения О главный вектор системы S не равен нулю, а ее главный момент или равен нулю или перпендикулярен главному вектору, т.е.
1. 
 0, 2.
0, 2. 
 0,
0,
 =0
=0 

 , то
, то
такая система приводится к равнодействующей. Эта равнодействующая по модулю и направлению равна главному вектору системы, а ее линия действия проходит через точку О` удовлетворяющую условию:
ОО`=  , ОО`
, ОО`  пл.(
пл.( ,
,  )
)
Следствие.
Единственным условием существования равнодействующей у системы сходящихся сил, плоской системы сил и системы параллельных сил является неравенство нулю главного вектора этих систем.
Теорема Вариньона
Формулировка:
Если для данной системы сил существует равнодействующая, то ее момент относительно произвольного центра (оси) равен сумме моментов всех сил этой системы относительно этого же центра (оси), т.е.
 (
(  )=
)= 
 (
( 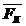 ),
),
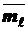 (
(  )=
)= 
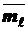 (
( 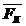 ),
),
Теорема Вариньона позволяет решать две задачи:






