Прежде необходимо убедиться, что эта равнодействующая существует
Если известна равнодействующая по модулю и направлению, то можно найти ее линию действия.
Выясним различия между главным вектором и равнодействующей системы.
Главный вектор 
| Равнодействующая 
|
=  
| = =
|
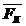
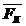
| 1.Характеристика системы S сил. (не сила!) | 1. Сила заменяющая действие системы сил S. |
| 2. Главный вектор существует для любой системы сил S | 2. Существует только для системы S, которая удовлетворяет условиям доказанной теоремы (не для всякой системы) |
| 3.Является вектором свободным. (первый статический инвариант) | 3. Является, как всякая сила, вектором скользящим. |
Приведение системы сил к паре
Теорема:
Если для произвольного центра приведения О главный вектор данной системы S (
) равен нулю, а ее главный момент не равен нулю, т.е.
=0, 
0,
То такая система приводится к паре. Момент этой пары равен по модулю и направлению главному моменту этой системы сил, т.е.
3.3 Приведение системы сил к динамическому винту.
Ведем понятие динамического винта.
Изобразим две картинки
 |
Совокупность силы и пары сил, момент которой параллелен силе, называется динамическим винтом, или динамой.
Сила стремится предать телу поступательное движение, пара – вращательное.
Следовательно, совместное их действие не тело вызывает винтовое движение.
Винтовое движение это самый общий случай движения твердого тела.
Теорема:
Если для произвольного центра приведения О главный вектор и главный момент данной системы сил не равны нулю и не перпендикулярны друг другу, т.е.
0, 0,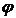 
,
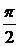То система приводится к динамическому винту. Сила винта по модулю и направлению равна главному вектору, а момент пары винта, наименьшему главному моменту.
Обозначение: D (
)
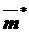Для того чтобы определить вид динамического винта мы должны рассмотреть характеристическое произведение.
Если Н больше нуля, то винт правый, если Н меньше нуля, то винт левый.
Если Н < 0, то >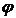 
- левый динамический винт
Если Н > 0, то 
< 
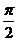- правый динамический винт
Второй способ: рассматривать угол между главным вектором и главным моментом, если он меньше 90 градусов винт правый, если больше 90 градусов, то винт левый.
Сводная таблица возможных случаев приведения системы сил к простейшему виду.
| № | Главные характеристические величины | Инварианты системы сил | Простейший вид системы |
| 1 | 
| 
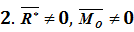
| Система приводится к равнодействующей
S  
ОО`=  , ОО`  пл.(, )
|
| 2 | 
| 
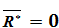
| Система приводится к паре
S ( ;  );
 (; )=  =
|
| 3 | 0, 0, ,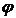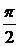
| 
| Система приводится к динамическому винту.
S D ( )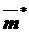
М´ = | МО cos |
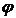ОО´ = 
|
| 
| Уравновешенная система |
