Характеристические величины системы сил.
Рассмотрим произвольную систему сил
S (
)
Введем величины, характеризующие совместное действие сил системы S
Как известно, действие одной силы характеризуется ее вектором силы 
и векторным моментом 
(
)относительно некоторой точки О. (Рис.1)
Совместное действие сил системы S принято характеризовать также двумя векторами:
1. Главным вектором - 
;
2. Главным моментом относительно некоторого центра - 
. (рис.2)
Главный вектор - это характеристическая величина, равная сумме всех сил данной системы.
Главный момент системы сил относительно некоторого центра О – сумма моментов всех сил системы относительно данного центра
Или
= 
(
),
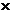
т.к.
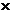
()= (2´)
 |
Введем главные моменты сил системы относительно координатных осей.
М X = mX()
MY= mY() (3)
MZ= mZ()
Введем дополнительную характеристику данной системы сил – характеристическое произведение.
Характеристическое произведение системы сил – скалярное произведение главного вектора на главный момент этой системы:
Где 
- угол между векторами и .
Величины Н, , характеризуют совместное действие системы сил S на твердое тело., поэтому будем их называть характеристическими величинами данной системы сил.
Эти величины помогут нам упрощать заданные системы сил при решении конкретных задач.
Лемма о параллельном переносе силы
Формулировка:
Всякую силу, приложенную к абсолютно твердому телу, можно переносить параллельно самой себе в любую другую точку тела, а чтобы ее действие на тело не изменилось, нужно добавить пару, которая называется присоединенной парой.
Доказательство:
Пусть к телу в точке А приложена сила 
. К данной силе , присоединим простейшую уравновешенную систему из сил 
и 
S (, ) 
0,
= =
, приложенных в произвольной точке О тела, как указано на рисунке.
Силы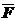 
; образуют пару.
Следовательно.
= S ( ,(
; )), причем
=
 |
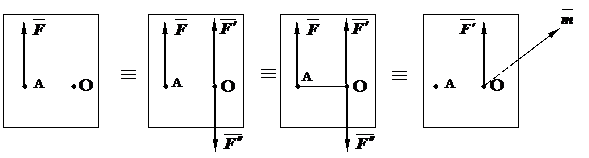Вместо пары (; ) будем изображать ее момент 
, который полностью характеризует действие этой пары.
Получили новую операцию над силой, она позволяет данную силу переносить параллельно самой себе в любую точку тела, прибавляя при этом пару, которая называется присоединенной парой.
Момент этой пары равен моменту силы приложенной в точке А относительно точки О.
(; )= ()
Основная теорема статики (Теорема Пуансо).
Формулировка:
Произвольная система сил S () эквивалентна системе, состоящей из силы, приложенной в произвольной точке О тела, и пары сил.
Сила по модулю и направлению равна главному вектору, а момент пары равен главному моменту данной системы сил относительно этой точки, т.е.
S ()= S 3 (
(
),
причем
= R 
; (; )= 
= .
Для доказательства используем Лемму о параллельном переносе силы. Каждую силу данной системы S () можно заменить силой в какой-то одной точке О тела и парой сил.
Назовем , элементами приведения системы сил S к центру О.
Замечание №1.
Для того чтобы практически заменить данную систему сил, силой и парой достаточно, в произвольной точке О построить главный вектор и главный момент системы сил.
Замечание № 2.
