5.1 Модель процесса искажения и восстановления изображений. Модели шума
Конечной целью восстановления изображений является повышение качества в некотором заранее предопределенном смысле. В отличие от процедур улучшения изображений, процесс восстановления изображений имеет в основном объективный характер. При восстановлении изображений делается попытка реконструировать или воссоздать изображение, которое было до этого искажено, используя априорную информацию о явлении, которое вызвало ухудшение изображения. В силу этого методы восстановления изображений основаны на моделировании процессов искажения и применения обратных процедур для воссоздания исходного изображения. Данный подход обычно включает в себя разработку критериев качества, которые дают возможность объективно оценить полученный результат.
Модель процесса искажения/восстановления изображения
На рисунке 41 представлена модель процесса искажения/восстановления изображения.
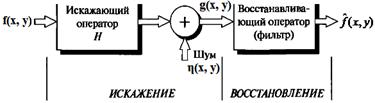
Рисунок 41 – Модель процесса искажения/восстановления изображения
Модель процесса искажения предполагает действие некоторого искажающего оператора H на исходное изображение f(x, y), что после добавления аддитивного шума дает искаженное изображение g(x, y). Задача восстановления состоит в построении некоторого приближения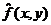 
исходного изображения по заданному (т.е. искаженному) изображению g(x, y), некоторой информации относительно искажающего оператора H, а также информации относительно аддитивного шума η (x, y). Необходимо достичь того, чтобы приближение 
было как можно ближе к исходному изображению f(x, y), что достигается при наличии максимальной информации об операторе H и о функции η (x, y). Основу подхода составляет использование операторов или фильтров, восстанавливающих изображение.
Искаженное изображение может быть представлено в пространственной области в виде:
g(x, y) = h(x, y) * f(x, y) +η (x, y)
где h(x, y) – функция, представляющая искажающий оператор в пространственной области.
В частотной области искаженное изображение может быть представлено как:
G(u, v)= H(u, v)· F(u, v)+ N(u, v)
Входящие в данное выражение частотные функции являются Фурье-образами соответствующих функций в пространственной области.
Модели шума
В силу того, что большая часть материала данной книги посвящена обработке цифровых изображений, то задачи восстановления изображений рассматриваются с момента получения уже искаженного цифрового изображения, поэтому все вопросы, касающиеся природы искажений, вносимых чувствительными элементами, цифровыми преобразователями и воспроизводящими устройствами рассматриваются лишь поверхностно.
Основными источниками шума на цифровом изображении являются сам процесс его получения (оцифровки), а также процесс передачи. Работа сенсоров зависит от различных факторов, таких как внешние условия в процессе получения изображения и качество самих сенсоров. Например, в процессе получения изображения с помощью ПЗС (прибор с зарядовой связью) матриц, основными факторами, влияющими на величину шума, являются уровень освещенности и температура сенсоров. В процессе передачи изображения могут искажаться помехами, возникающими в каналах связи, например, при передаче изображений по беспроводным сетям, оно может быть искажено в результате воздействия различных атмосферных возмущений.
При рассмотрении шумов важными являются параметры, определяющие пространственные характеристики шума, а также наличие или отсутствие корреляции между шумом и изображением. Под частотными характеристиками шума понимаются свойства его Фурье-спектра. Например, шум, спектр которого является постоянной величиной, называется обычно “белым шумом”. Происхождение названия данного вида шума связано с физическими свойствами белого света, который содержит практически все частоты видимого спектра в равных пропорциях. Для упрощения рассматриваемых задач и с учетом незначительной потери в качестве их решений будем в дальнейшем полагать, что шумы изображения не зависят от пространственных координат и не коррелируют с самим изображением.
Наиболее часто модели шумов, присутствующих на изображениях, представляют в пространственной области. Данное представление основано на статистических свойствах значений яркости компонентов шума. Эти значения яркости могут рассматриваться как случайные величины, характеризующиеся функцией плотности распределения вероятностей.
Пусть задана некоторая случайная переменная Z. Функция распределения вероятностей F(Z) случайной величины Z представляет собой функцию, значение которой для каждого z является вероятностью события, заключающегося в том, что случайная величина Z принимает значения, меньшие переменной z, т.е. функцию вида F(z) = P(Z< z). Данная функция представляет собой неубывающую функцию переменной z, изменяющуюся от F (−∞)=0 до F (+∞)=1. Для случайной величины с непрерывной и дифференцируемой функцией распределения F(z) можно найти дифференциальный закон распределения вероятностей, выражаемый как производная от функции F(z), т.е. как p(z) = F′(z). Данная зависимость называется функцией плотности распределения вероятностей.
Далее будут рассмотрены примеры функций плотности распределения вероятностей применительно к наиболее распространенным моделям шумов, встречающихся при обработке цифровых изображений.
Гауссов шум
Математическая простота, характерная для работы с моделями гауссова шума (или нормального шума), как в пространственной, так и в частотной области, обусловила широкое распространение этих моделей на практике.
Функция плотности распределения вероятностей гауссовой случайной величины z задается выражением:
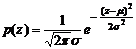
где: z – значение яркости, μ – среднее значение случайно величины z, σ – среднеквадратичное отклонение случайной величины z.
На рисунке 42 А приведен график функции плотности распределения гауссова шума.
Шум Релея
Функция плотности распределения вероятностей шума Релея задается выражением:
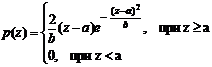
Среднее и дисперсия для этого распределения имеют вид:
На рисунке 42 Б приведен график функции плотности распределения шума Релея.
Шум Эрлея (гамма шум)
Функция плотности распределения вероятностей шума Эрланга определяется как:
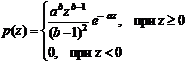
где: a>0, b – положительное целое число.
Среднее и дисперсия для этого распределения имеют вид:
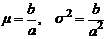
На рисунке 42 В приведен график функции плотности распределения шума Эрланга.
Рисунок 42 – Функции плотности распределения вероятностей основных видов шумов
Экспоненциальный шум
Функция плотности распределения вероятностей экспоненциального шума задается выражением:
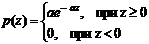
где: a>0
Среднее значение и дисперсия для этого распределения имеют вид:
На рисунке 42 Г приведен график функции плотности распределения экспоненциального шума. Заметим, что экспоненциальное распределение является частным случаем распределения Эрланга при b =1.
Равномерный шум
Функция плотности распределения вероятностей равномерного шума задается выражением:
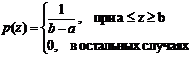
Среднее значение и дисперсия равномерного распределения равно:
На рисунке 42 Д приведен график функции плотности распределения равномерного шума.
Импульсный шум
Функция плотности распределения вероятностей (биполярного) импульсного шума определяется выражением:
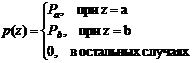
Если b > a, то пиксель с яркостью b выглядит как светлая точка на изображении. Пиксель с яркостью a выглядит, наоборот, как темная точка. Если одно из значений вероятности (Pa или Pb) равно нулю, то импульсный шум называется униполярным. Часто данный вид шума называют шумом типа “соль и перец”.
Значения импульсов шума могут быть как положительные, так и отрицательные. При оцифровке изображения обычно происходит масштабирование и ограничение значений яркости. Поскольку величина связанных с импульсным шумом искажений, как правило, велика по сравнению с величиной полезного сигнала, импульсный шум после оцифровки принимает экстремальные значения, что соответствует появлению абсолютно черных и белых точек на изображении. Обычно предполагается, что значения a и b являются интенсивностями шума в том смысле, что они равны максимальному и минимальному значениям, которые в принципе могут присутствовать в оцифрованном изображении. В результате отрицательные импульсы выглядят как черные точки на изображении, положительные импульсы – как белые точки. На рисунке 42 Е представлен график функции плотности распределения импульсного шума.
Рисунок 43 – Изображения и гистограммы, полученные в результате добавления различного рода шумов
Таким образом, рассмотренные модели различных видов шумов представляют собой набор эффективных средств, которые позволяют моделировать искажения, связанные с широким диапазоном встречающихся на практике шумов. Например, гауссов шум возникает на изображении в результате воздействия таких факторов, как шум в электронных цепях или шум сенсоров, возникающий из-за недостатка освещения или высокой температуры. Распределение Релея применяется при моделировании шума, который возникает на снимках, снятых с большого расстояния. Экспоненциальное и гамма распределения соответствуют шуму на изображениях, получаемых с использованием лазеров. Импульсный шум наблюдается, когда в процессе получения изображения имеют быстрые переходные процессы, например, такие как неправильная коммутация.
На рисунке 43 представлены изображения, полученные в результате прибавления к тестовому изображению шумов определенного типа; под каждый изображением приведена соответствующая данному изображению гистограмма. Несложно убедиться в том, что гистограммы зашумленных изображений соответствуют виду графиков функций плотности распределения вероятностей шумов.
Необходимо заметить, что по внешнему виду зашумленного изображения невозможно определить тип шума, присутствующего на изображении, за исключением случая присутствия импульсного шума. В то время как гистограммы соответствующих зашумленных изображений существенно отличаются друг от друга, что наглядно демонстрирует преимущество использования анализа гистограмм при исследовании зашумленных изображений.
Периодический шум
Причиной появления периодического шума обычно являются электрические или электромеханические помехи во время получения изображения. Данный вид шумов может быть существенно уменьшен при помощи методов частотной фильтрации. Присутствие периодического шума на изображении можно определить путем анализа Фурье спектра зашумленного изображения. Преобразование Фурье от изображения, искаженного периодическим шумом гармонического происхождения, представляет собой наложенную на спектр исходного изображения пару сопряженных импульсов, расположенных в центрально-симметричных точках частотной области, отвечающих частотам гармонической волны.
Построение оценок для параметров шумов
Оценка параметров периодического шума обычно осуществляется путем анализа Фурье-спектра изображения. Периодический шум приводит к появлению пиков в частотной области, которые часто обнаруживаются при визуальном анализе спектре.
Параметры функции плотности распределения вероятностей шума могут быть частично известны исходя из технических характеристик сенсоров, однако зачастую необходимо оценивать эти параметры для конкретной системы, использованной при получении данного изображения. В этом случае одним из простейших способов изучения характеристик системы регистрации изображений, связанных с шумами, заключается в том, чтобы получить набор изображений однородных тестовых объектов. В случае обычной оптической системы, таким объектом целесообразно выбрать сплошную равномерно освещенную серую область. Полученные таким образом изображения достаточно полно характеризуют шумы системы.
В тех случаях, когда доступны исключительно изображения, ранее сформированные системой, рассмотрение гистограмм небольших участков изображения примерно постоянной яркости позволяет оценить параметры функции плотности распределения вероятностей шума. Для рассматриваемых участков изображения вычисляют среднее значение и дисперсию яркости на основе применения следующих статистических формул:
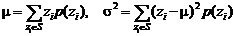
где zi – значения яркости элементов части изображения S, p(zi) – соответствующие нормализованные значения гистограммы.
Вид гистограммы определяет, какая из существующих функций плотности распределения вероятностей является наиболее подходящей. Например, в том случае, если форма гистограммы близка к гауссовой функции плотности распределения вероятностей, то необходимо определить значения среднего и дисперсии. Для распределения других типов рассматриваются выражения для среднего и дисперсии как уравнения для параметров a и b, решение которых позволит найти параметры распределения.
5.2 Подавление шумов – пространственная фильтрация
В том случае, если искажение изображения обусловлено исключительно наличием шума, то модель искаженного изображения можно представить в виде аддитивной суммы шума и исходного изображения:
Или аналогично в частотной области:
В общем случае, слагаемое, описывающее шум – η (x, y) или N(u, v) неизвестно, поэтому его нельзя просто вычесть из функции g(x, y) или G(u, v). В случае периодического шума спектр G(u, v) дает возможность оценить величину N(u, v), в этом случае в целях построения приближения исходного изображения, величина N(u, v) может быть вычтена из функции G(u, v).
В тех ситуациях, когда на изображении присутствует только аддитивный шум, пространственная фильтрация является лучшим из возможных методов восстановления.
Усредняющие фильтры
Фильтр, основанный на вычислении среднего арифметического
Данный тип фильтра называется среднеарифметическим фильтром и является простейшим среди усредняющих фильтров. Пусть Sxy обозначает прямоугольную окрестность – множество координат точек изображения размерами m × n с центром в точке (x, y). Процедура фильтрации предполагает вычисление среднего арифметического значения искаженного изображения g (x, y) по окрестности Sxy. Значение восстановленного изображения в произвольной точке (x, y) представляет собой среднее арифметическое значений в точках, принадлежавших окрестности Sxy:
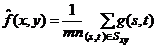
Данная операция может быть реализована в виде свертки с маской, все коэффициенты которой равны 1/ m · n. Усредняющий фильтр сглаживает локальные вариации яркости на изображении, уменьшение шума происходит в результате этого сглаживания.
Фильтр, основанный на вычислении среднего геометрического
Изображение, восстановленное с использованием среднегеометрического фильтра, задается выражением:
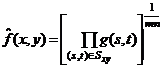
Применение среднегеометрического фильтра приводит к сглаживанию, сравнимому с тем, которое достигается при использовании среднеарифметического фильтра, но при этом теряется меньше деталей изображения.
Фильтр, основанный на вычислении среднего гармонического
Результат обработки с применением среднегеометрического фильтра определяется выражением:
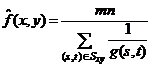
Среднегармонический фильтр применим для обработки изображений, искаженных гауссовым шумом, а также так называемым, “белым импульсным шумом”, т.е. когда значение шума соответствует появлению белых точек на изображении, но не работает в случае появления “черного импульсного шума”, когда значение шума соответствует появлению черных точек.
Фильтр, основанный на вычислении среднего контргармонического
Обработка с применением операции вычисления среднего контргармонического описывается выражением:
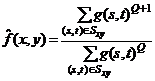
где Q называется порядком фильтра.
Данный тип усредняющего фильтра хорошо приспособлен для уменьшения или почти полного устранения импульсного шума. При положительных значениях Q фильтр устраняет “черную” часть импульсного шума, при отрицательных – “белую” часть импульсного шума. Заметим, что контргармонический фильтр при Q =0 сводится к среднеарифметическому фильтру, а при Q =0 – к среднегармоническому фильтру.
Таким образом, в заключении необходимо сказать, что среднеарифметические и среднегеометрические фильтры наиболее приемлемы для фильтрации случайных шумов типа гауссова или равномерного. Контргармонические фильтры подходят для фильтрации импульсного шума, но их применение затрудняется необходимостью наличия априорной информации о типе импульсного шума (черный или белый), поскольку необходимо выбрать правильный знак порядка фильтра.
Фильтры, основанные на порядковых статистиках
Фильтры, основанные на порядковых статистиках, представляют собой пространственные Фильтры, вычисление отклика которых требует предварительного упорядочивания или ранжирования значений пикселей, заключенных внутри обрабатываемой фильтром области. Отклик фильтра в любой точке определяется по результатам упорядочивания.
Медианные фильтры
Наиболее известным из фильтров, основанных на порядковых статистиках, является медианный фильтр. Действие этого фильтра состоит в замене значения в точке изображения на медиану значений яркости в окрестности этой точки:
Медианные фильтры отлично справляются с задачей подавления некоторых видов случайных шумов, и при этом обеспечивают меньшее размытие изображений по сравнению с линейными сглаживающими фильтрами того же размера. Медианные фильтры особенно эффективны при наличии как биполярного, так и униполярного импульсного шума.
Фильтры, основанные на выборе максимального и минимального значения
Медиана выборки представляет собой 50-й перцентиль упорядоченного набора чисел, однако, использование других статистических характеристик предоставляет ряд дополнительных возможностей подавления шумов на изображении.
Использование 100-го перцентиля приводит к фильтру, основанному на выборе максимального значения или фильтра максимума, который задается выражением:
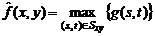
Такой фильтр полезен при обнаружении наиболее ярких точек на изображении. Применение такого фильтра приводит к уменьшению “черного” импульсного шума, так как в процессе фильтрации из окрестности Sxy выбирается максимальное значение.
Использование 0-го перцентиля приводит к фильтру, основанному на выборе минимального значения или фильтре минимума:
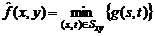
Данный фильтр полезен при обнаружении наиболее темных точек на изображении. Применение фильтра минимума приводит к уменьшению униполярного “белого” импульсного шума вследствие операции выбора минимума.
Фильтр срединной точки
Применение фильтра срединной точки заключается в вычислении среднего между максимальными и минимальными значениями в соответствующей окрестности:
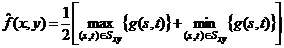
Такой фильтр объединяет в себе методы порядковых статистика и арифметического усреднения. Фильтрация подобного типа наиболее эффективна при наличии случайно распределенных шумов, таких как гауссов или равномерный.
Фильтр, основанный на вычислении усеченного среднего
Предположим, что из изображения были удалены d /2 наименьших и d /2 наибольших значений яркости из множества всех значений функции g(s, t) в окрестности Sxy. Пусть тогда gr(s, t) представляет собой оставшиеся элементы изображения, количество которых равно (m × n − d). Фильтр, действие которого заключается в усреднении оставшихся значений, называется фильтром усеченного среднего:
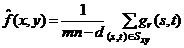
Значение d может изменяться в диапазоне от 0 до m × n −1. В случае d =0, фильтр усеченного среднего сводится к среднеарифметическому фильтру, в случае, d /2=(m × n −1)/2, фильтр сводится к медианному фильтру. Применение фильтра усеченного среднего наиболее целесообразно при искажении изображения комбинацией импульсного и гауссова шумов.
Адаптивные фильтры
Адаптивным фильтром является такой фильтр, поведение которого изменяется в зависимости от статистических свойств изображения внутри области действия фильтра, которая определяется прямоугольной m × n окрестностью Sxy. К преимуществам адаптивных фильтров по сравнению с ранее рассмотренными видами фильтров является то, что их возможности обработки зашумленных изображений существенно превосходят возможности неадаптивных фильтров, что достигается за счет усложнения практической реализации таких фильтров.
Адаптивные локальные фильтры подавления шума
Простейшими локальными характеристиками случайной величины являются ее среднее значение и дисперсия. Данные параметры изображений или его некоторой области составляют основу при разработке адаптивных фильтров, в силу того, что указанные величины связаны с внешним видом обрабатываемого изображения: среднее значение определяет среднюю яркости рассматриваемой области, а дисперсия – меру среднего отклонения в этой области.
Отклик адаптивного фильтра в некоторой точке (x, y), которая является центром окрестности Sxy, должен определяться следующими величинами:
1) значением изображения с шумом в точке (x, y);
2) дисперсией шума σ2η, превращающего исходное изображение f (x, y) в искаженное изображение g (x, y);
3) локальным средним mL по значениям в окрестности Sxy;
4) локальной дисперсией σ2 L, по значениям в окрестности Sxy;
Поведение адаптивного фильтра должно определяться следующими условиями:
1. Если дисперсия шума σ2η=0, то отклик фильтра должен быть равен значению g (x, y), что соответствует тривиальному случаю нулевого шума, когда g (x, y) равно f (x, y).
2. Если локальная дисперсия σ2 L много больше σ2η, то значение отклика фильтра должно быть порядка g (x, y). Большое значение локальной дисперсии обычно связано с наличием контуров, которые должны быть сохранены.
3. Если обе дисперсии принимают значения одного порядка, то отклик фильтра должен быть равен среднему арифметическому значений в окрестности Sxy. Условие выполняется в том случае, когда статистические характеристики данной локальной области и изображения в целом совпадают, и локальный шум должен быть уменьшен, для чего используется простое усреднение.
Адаптивный фильтр, удовлетворяющий перечисленным условиям, может быть задан следующим выражением:
Единственной величиной, которая должна быть заранее известна или оценена, является полная дисперсия шума σ2η. Остальные входящие в приведенное выражение величины вычисляются для каждой точки (x, y) по значениям элементов изображения в окрестности Sxy с центром в этой точке.
Общее уменьшение шума на изображении при обработке адаптивными локальными фильтрами обычно сопоставимо с уменьшением шума при использовании арифметических сглаживающих фильтров, однако, изображение, получаемое после обработки с помощью адаптивного фильтра, является намного более резким.
Если оценка дисперсии шума слишком занижена относительно истинного значения, то в результате обработки получаемое изображение будет незначительно отличаться от исходного зашумленного изображения. В том случае, если оценка наоборот завышена, то отклик адаптивного локального фильтра будет очень близок или даже совпадать с откликом среднеарифметического фильтра, что, в конечном счете, приведет к излишнему размытию обрабатываемого изображения.
Адаптивные медианные фильтры
Обычнее медианные фильтры обеспечивают приемлемый результат фильтрации импульсных шумов до тех пор, пока пространственная плотность импульсного шума невелика (как правило – Pa и Pb не превышают 0,2). Адаптивная медианная фильтрация позволяет обрабатывать изображения, искаженные шумами большей интенсивности. Дополнительным преимуществом адаптивного медианного фильтра, по сравнению с обычным фильтром, является гораздо меньшее искажение контуров присутствующих на изображении объектов.
Адаптивный медианный фильтр изменяет размеры окрестности Sxy во время работы в соответствии с определенными условиями. Введем следующие обозначения:
zmin – минимальное значение яркости в окрестности Sxy; zmax – максимальное значение яркости в окрестности Sxy; zmed – медиана значений яркости в окрестности Sxy; zxy – значения яркости в точке (x, y). Smax – максимальный допустимый размер Sxy.
Алгоритм медианной фильтрации состоит их двух ветвей, обозначенных ниже как ветвь А и ветвь Б, и его действие заключается в следующем:
| Ветвь А: | A1 = zmed−zmin; A2 = zmed−zmax; Если A1 >0 и A2 <0, то переходим к ветке Б; Иначе увеличить размер окрестности; Если размер окрестности Sxy ≤ Smax – повторить ветвь А; Иначе результат равен zxy |
| Ветвь Б: | B1 = zxy − zmin; B2 = zxy − zmax; Если B1 >0 и B2 <0, результат равен zxy Иначе результат равен zmed |
Применение данного алгоритма преследует три основные цели: удалить биполярный импульсный шум, обеспечить сглаживание шумов других типов, свести к минимуму искажения границ объектов на изображении. Значения zmin и zmax воспринимаются алгоритмом статистически как значения импульсных составляющих шума.
Ветвь А алгоритма преследует цель определить, является ли медиана zmed импульсом или нет. Если условие zmin< zmed< zmax выполнено, то zmed не может быть импульсом. В этом случае алгоритм переходит на ветвь Б и осуществляется проверка, является ли импульсом значение zxy в той точке, которая отвечает центру окрестности. Если условия B1 >0 и B2 <0 выполнены, то zmin< zxy< zmax, то значение zxy не является импульсным. В этом случае алгоритм дает на выходе неизменное значение zxy. Сохранение значения яркости в таких точках минимизирует искажения, вносимые обработкой изображения. Если хотя бы одно из условий B1 >0 или B2 <0 нарушено, то либо zxy = zmin, либо zxy = zmax. В обоих случаях значения является экстремальным, и алгоритм дает на выходе значение медианы zmed, которое, как следует из результатов работы ветви А, не является значением импульсного шума. Последняя операция в точности соответствует процедурам обычного медианного фильтра. Отличие заключается в том, что обычный медианный фильтр заменяет значения в каждой точке на значение медианы по соответствующей окрестности, что и приводит к излишним искажениям деталей на изображении.
В том случае, если вычисленная при работе ветви А медиана является импульсом, т.е. нарушено условие перехода к ветви Б, то в таком случае алгоритм предполагает увеличение размеров окрестности и повторение вычислений по ветви А. Процесс повторяется до тех пор, пока либо не будет найдена медиана, отличная от импульса, либо размеры окрестности не достигнут максимального допустимого размера. В последнем случае алгоритм на выходе выдает значение zxy, при этом нет гарантий, что это значение не является импульсным. Чем меньше плотности вероятности шума Pa и Pb, или чем больше максимальный допустимый размер окрестности Smax , тем меньше вероятность такого преждевременного (без перехода к ветви Б) выхода из алгоритма. При увеличении плотности импульсов необходимо будет использовать окрестность большего размера для устранения шумовых пиков.
После получения значения обрабатываемого элемента изображения, центр окрестности смещается в позицию следующего элемента, алгоритм инициализируется вновь и применяется к пикселям внутри окрестности Sxy, находящейся в новом положении.
Выбор максимального допустимого размера окрестности в алгоритме зависит тот конкретного приложения. Оптимальную оценку данного параметра можно получить, экспериментируя предварительно с обычными медианными фильтрами различных размеров, что позволит также оценить примерные результаты от применения адаптивного алгоритма медианной фильтрации.
Необходимо заметить, что при обработке биомедицинских изображений предъявляются жесткие требования к минимизации вносимых искажений применяемыми алгоритмами и фильтрами, в силу этого, адаптивные медианные фильтры находят гораздо более частое применение в задачах медицинской диагностики при анализе изображений, чем простой медианный фильтр, действие которого на изображение зачастую приводит к появлению крайне нежелательных нелинейных эффектов, проявляющихся в утончении или утолщении контуров объектов изображения, что может привести к постановке неверного диагноза.
5.3 Подавление периодического шума – частотная фильтрация
Для уменьшения или полного устранения периодического шума на изображении применяются специализированные полосовые, режекторные, узкополосные полосовые и узкополосные режекторные фильтры, реализованные в частотной области.
Режекторные фильтры
Режекторные фильтры удаляют или ослабляют частоты в кольцевой полосе вокруг начала координат преобразования Фурье. Передаточная функция идеального режекторного фильтра задается выражением:
где: D (u, v) – расстояние, измеряемое от центра частотного прямоугольника, W – ширина кольца, D 0 – радиус окружности, проходящей через его середину.
Передаточная функция режекторного фильтра Баттерворта порядка n задается выражением:
Передаточная функция режекторного гауссова фильтра задается выражением:
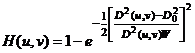
Изображение типового режекторного фильтра типа Баттерворта приведено на рисунке 44.
Рисунок 44 – Изображение режекторного фильтра Баттерворта
Режекторные фильтры весьма эффективны при обработке изображений, искаженных гармоническим шумом. Радиус и ширину режекторного фильтра необходимо выбирать таким образом, чтобы шумовые импульсы полностью попадали в соответствующую область. Для уменьшения нежелательных искажений обрабатываемого изображения необходимо удалять как можно меньшую часть Фурье-преобразования, необходимо использовать режекторные с крутой и узкой передаточной характеристикой. Необходимо заметить, что фильтрация в пространственной области с использованием масок небольшого размера не позволяет достичь аналогичного результата.
Полосовые фильтры
Полосовые фильтры осуществляют операцию противоположную режекторным фильтрам. Передаточная функция полосового фильтра Hbp (u, v) может быть получена из передаточной функции соответствующего режекторного фильтра при помощи выражения:
Hbp (u, v)=1− Hbr (u, v)
Полосовая фильтрация обычно не используется для улучшения изображений непосредственно, поскольку, как правило, в результате ее применения слишком большая часть деталей оказывается удаленной. Тем не менее, полосовая фильтрация оказывается весьма полезной для отделения тех компонентов, которые обусловлены частотными составляющими в выбранном диапазоне, в том числе частотными составляющими гармонического шума.
Таким образом, полосовая фильтрация позволяет выделять шумовую составляющую изображения, что позволяет серьезно упростить процедуру анализа шума, которая может быть осуществлена независимо от содержательной части самого изображения.
Узкополосные фильтры
Узкополосные полосовые фильтры и узкополосные режекторные фильтры соответственно пропускают или не пропускают частоты в определенных окрестностях своих центральных частот.
В силу свойств симметрии преобразования Фурье для получения вещественных результатов фильтрации любой фильтр должен быть симметричен относительно начала координат – центра частотного прямоугольника.
Передаточная функция идеального узкополосного режекторного фильтра радиуса D 0 с центрами в точке (u0, v0) и, в силу симметрии, в точке (− u0, − v0) задается выражением:
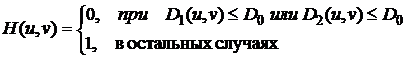
где:
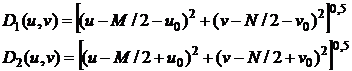
Центр частотного прямоугольника находится в точке с координатами (M/2, N/2), поэтому значения (u0, v0) отсчитываются от этого центра частотного прямоугольника.
Передаточная функция узкополосная режекторного фильтра Баттерворта порядка n задается выражением:
Передаточная функция гауссова узкополосного фильтра Баттерворта порядка n имеет вид:
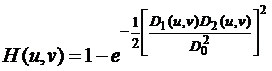
Узкополосные полосовые фильтры, пропускающие частотные составляющие в окрестностях своих центральных частот, могут быть получены тем же способом, что и полосовые фильтры, их передаточные функции могут быть заданы выражением:
Hnp (u, v)=1− Hnr (u, v)
где: Hnp (u, v) – передаточная функция узкополосного полосового фильтра, соответствующего узкополосному режекторному фильтру с передаточной функцией Hnr (u, v).
Использование узкополосных фильтров позволяет уменьшить шум на изображениях, не приводя при этом к заметному сглаживанию, что делает данный тип фильтров более предпочтительным для использования по сравнению с обычными полосовыми или режекторными фильтрами.
Оптимальная узкополосная фильтрация
Зачастую помехи на изображении не имеют ясно выраженной структуры, что затрудняет непосредственное применение частотной фильтрации. Например, изображения, полученные при помощи электрооптических приборов, иногда бывают искажены в результате интерференции и усиления сигналов низкого уровня в электронном тракте регистрирующей системы, в результате чего на изображении возникают двумерные периодические помехи сложной природы, т.е. такие помехи содержат более чем одну периодическую компоненту.
Если помехи, присутствующие на изображении, содержат несколько составляющих, то рассмотренные ранее методы фильтрации не всегда применимы, так как могут привести к потере слишком большого количества информации на изображении в процессе фильтрации. Частотные составляющие помех, как правило, не являются узко локализованными вблизи некоторых отдельных точек в частотной области, и находятся в достаточно широкой частотной области, содержащей соответствующую информацию о структуре исходного изображения. Нахождение таких областей классическими методами Фурье-анализа далеко не всегда является простой задачей. Для решения подобных проблем разработаны методы фильтрации, которые являются оптимальными в том смысле, что обеспечивают минимизацию локальной дисперсии восстановленного изображения.
Суть оптимальных методов фильтрации заключается в том, чтобы получить в виде отдельного изображения основной вклад, привносимый помехой и вычесть из исходного искаженного изображения некоторую непостоянную весовую долю полученного изображения помехи.
Первый шаг метода состоит в выделении основных частотных составляющих помехи, что может быть осуществлено при помощи узкополосного фильтра H (u, v), который пропускает частоты в окрестностях каждого связанного с помехой частотного пика. Фурье-преобразование шумовой составляющей определяется выражением:
N (u, v)= H (u, v)· G (u, v)
где: G (u, v) – Фурье-преобразование искаженного изображения.
Построение фильтра H (u, v) требует принятие решения о том, является ли каждый конкретный пик в частотной области шумовым пиком или нет. По этой причине узкополосный фильтр подбирается, как правило, интерактивно на основе визуального анализа спектра изображения G (u, v). После того, как конкретный фильтр выбран, соответствующее изображение шума в пространственной области может быть следующим образом:
Основная проблема заключается в том, что фильтрация обычно позволяет получить некоторое приближение к функции, определяющей связанную с помехой составную часть изображения. Эффект, связанный с отличием построенного приближения η(x, y) от реальной помехи, может быть уменьшен, если при построении приближения для неискаженного изображения f (x, y) из искаженного изображения g (x, y) вычитать некоторую взвешенную долю функции η(x, y):
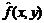= g (x, y)− w (x, y)·η(x, y)
где: 
– приближение для неискаженного изображения f (x, y), w (x, y) – весовая функция или функция модуляции.
Задача метода состоит в таком выборе весовой функции w (x, y), чтобы полученный результат оказался в некотором смысле оптимальным. Одним из критериев выбора функции w (x, y) заключается в том, чтобы величина локальной дисперсии получаемого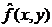 
приближения по заданной окрестности принимала минимальное значение в каждой точки (x, y).
Рассмотрим окрестность некоторой точки (x, y) размерами (2а+1)×(2b+1), локальная дисперсия функции в точке с координатами может быть получена следующим образом:
где: 
– среднее значение функции 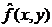по окрестности, определяемое как:
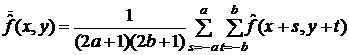
Запишем выражение для локальной дисперсии в следующем виде:
Предположим, что функция w (x, y) практически постоянна в пределах окрестности, т.е.:
w (x+ s, y+ t)= w (x, y)
при − a ≤ s ≤ a и − b ≤ s ≤ b. При этом в окрестности будет иметь место следующее равенство:
Представим выражение для локальной дисперсии как:
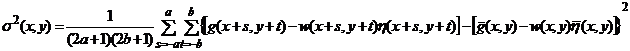Для того, чтобы найти функцию w (x, y), для которой реализуется экстремум (минимум) функционала σ2(x, y), нужно решить следующее уравнение относительно w (x, y):
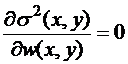
Решение данного уравнения относительно w (x, y) имеет вид:
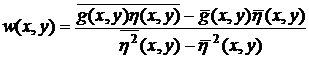
В силу предположения о том, что функция w (x, y) является постоянной в пределах окрестности, то нет необходимости вычислять значения этой функции для всех точек обрабатываемого изображения. Вместо этого можно вычислить по одному значению w (x, y) в некоторой точке каждого из непересекающихся его фрагментов (предпочтительно в центральной точке фрагмента), а затем использовать это значение при обработке всех точек изображения, содержащихся в этом фрагменте.
5.4 Оценка искажающей функции
Существует три основных способа оценки искажающей функции (или ядра искажающего оператора) для последующего ее использования при восстановлении изображений:
1) визуальный анализ;
2) эксперимент;
3) математическое моделирование.
В силу того, что искажающая функция редко бывает известна полностью, процесс восстановления изображения с использованием приближения искажающей функции, полученного некоторым образом, иногда называют процессом реконструкции “вслепую”.
Оценка на основе визуального анализа изображения
Предположим, что имеется искаженное изображение, но информация об искажающей функции H отсутствует. Один из способов оценить эту функцию состоит в выделении информации непосредственно из изображения. Например, если изображение является размытым, то можно рассмотреть небольшой фрагмент, содержащий простую структуру, такую как часть некоторого объекта и фон. С целью уменьшения влияния шума на наблюдения, необходимо выбирать ту область изображения, которая содержит полезный сигнал большой амплитуды, используя яркости объекта и фона, можно приблизительно построить неразмытое изображение тех же размеров и с теми же особенностями, что и рассматриваемая часть исходного изображения. Обозначим рассматриваемую часть изображения как gs (x, y) и построенное изображение (которое в действительности представляет собой наше приближение для части неискаженного изображения в рассматриваемой области) как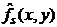 
. Предполагая, что влияние шума пренебрежимо мало в силу выбора области с большим полезным сигналом, можно получить выражение следующего вида:
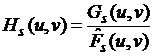
где: Hs (u, v) – Фурье-преобразование оцениваемой искажающей функции, Gs (u, v) – Фурье-преобразование части изображения gs (x, y), 
– Фурье-преобразование построенного изображения.
Исходя из свойств функции Hs (u, v) можно сделать выводы о свойствах полной искажающей функции H (u, v).
Оценка на основе эксперимента
Если оборудование, которое использовалось для получения рассматриваемого изображения или аналогичное ему является доступным, то представляется возможным получить точную оценку искажающей функции. Для этого необходимо подобрать параметры системы, чтобы искажения на получаемых с ее помощью изображениях, похожих по сценарию на подлежащее восстановлению изображении, как можно лучше соответствовали искажениям на этом изображении. На следующем этапе необходимо сформировать импульсный отклик (ядро искажающего оператора), для чего нужно получить изображение импульса (меленькой яркой точки), используя систему с подобранными значениями параметров.
Импульс симулируется яркой световой точкой, чтобы уменьшить влияние шума, яркость импульса должна быть как можно больше. Учитывая, что Фурье-преобразование импульса представляет константу, можно получить следующее выражение:
где: G (u, v) – Фурье-преобразование полученного изображения, А – константа, описывающая величину яркости импульса.
Оценка на основе моделирования
Моделирование искажений, проявляющихся на изображении, позволяет проникнуть в суть задачи восстановления изображений, в некоторых случаях, моделирование позволяет учесть внешние условия, вызывающие появление искажений. Другим важным аспектом моделирования является построение математической модели непосредственно из основных принципов получения изображения. При создании такого рода математических моделей зачастую необходимо наличие информации о природе возникновения артефактов на изображении, например, моделирование смазывания или размытия на изображении, вследствие движения изображения сцены относительно регистрирующей системы в процессе регистрации и формировании изображения объекта, основывается на том, что известен закон движения объекта.
Создание корректных и адекватных математических моделей, описывающих процесс проявления различного рода артефактов на биомедицинских изображениях является нетривиальной задачей и требует индивидуального подхода в зависимости от той или иной ситуации формирования изображения.
5.5 Инверсная фильтрация
Задача восстановления изображения значительно упрощается, если известна или определена с помощью ранее описанных методов искажающая функция (ядро или оператор H). Простейшим способом восстановления изображения является инверсная фильтрация, которая предполагает получение оценки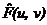 
Фурье-преобразования исходного изображения делением Фурье-преобразования искаженного изображения на частотное представление искажающей функции: (деление подразумевается как поэлементная операция).
Введем величину N (u, v), определяемую как Фурье-преобразование функции присутствующего на изображении шума η(x, y), и справедливым является следующее выражение:
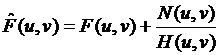
Данное выражение показывает, что обладая информацией исключительно об искажающей функции, невозможно восстановить неискаженное исходное изображение (с помощью операции обратного Фурье-преобразования функции F (u, v)), так как функция N (u, v) представляет собой Фурье-преобразование случайной величины и является неизвестной. Как правило, значение искажающей функции становятся пренебрежимо малыми на больших частотах, в силу этого функция H (u, v) может принимать нулевые или близкие к нулевым значениям, поэтому вклад второго слагаемого становится доминирующим, что дополнительно затрудняет процесс восстановления изображения.
Одним из способов устранения указанных трудностей состоит в том, чтобы ограничить частоты фильтра значениями вблизи начала координат, так как полагается, что функция H (u, v) обращается в нуль вне некоторой области вблизи начала координат.
Для реализации этого способа достаточно умножить правую часть указанного выше равенства на передаточную функцию некоторого идеального низкочастотного фильтра. Как известно, значение H (0, 0) равно среднему значению функции h (x, y) и обычно является наибольшим значением H (u, v) в частотной области, поэтому ограничиваясь рассмотрением частот вблизи начала координат, уменьшается вероятность встреть нулевое значение.
Инверсная фильтрация обладает очевидным недостатком – отсутствие информации о статистических свойствах присутствующих на изображении шумов при восстановлении, что делает данный метод слабо применимым на практике.
5.6Винеровская фильтрация
Рассмотренный ранее метод инверсной фильтрации не обеспечивает корректной работы по отношению к шуму. Одним из наиболее эффективных методов восстановления изображения, основанного одновременно на учете свойств искажающей функции и статистических свойств шума в процессе восстановления, является винеровская фильтрация или фильтрация методом минимизации среднеквадратического отклонения.
Данный метод основан на рассмотрении изображений и шума как случайных процессов, и задача формулируется следующим образом: необходимо найти такую оценку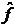 
для неискаженного изображения f, чтобы среднеквадратическое отклонение этих величин друг от друга было минимальным. Среднеквадратическое отклонение e задается формулой:
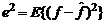
где: E {·} обозначает математическое ожидание своего аргумента.
Предполагается, что выполнены следующие условия:
1) шум и неискаженное изображение не коррелированны между собой;
2) либо шум, либо неискаженное изображение имеют нулевое среднее значение;
3) оценка линейно зависит от искаженного изображения.
При выполнении этих условий минимум среднеквадратического отклонения достигается для оценивающей исходное изображении функции, заданной в частотной области следующим образом:
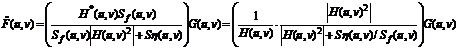
где: G (u, v) – Фурье-преобразование искаженного изображения; H (u, v) – частотное представление искажающей функции, H* (u, v) – комплексное сопряжение H (u, v); 
– энергетический спектр искажающей функции;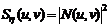 
– энергетический спектр шума; 
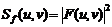– энергетический спектр неискаженного изображения.
Приведенный результат был впервые получен Н. Винером, и метод известен как оптимальная фильтрация по Винеру. Фильтр, представленный передаточной функцией внутри скобок, называется винеровским фильтром. Анализируя приведенное выражение, необходимо заметить, что для винеровского фильтра отсутствует проблема обращения в нуль спектра искажающей функции, за исключением того случая, когда функции H (u, v) и S η(u, v) обращаются в некоторых точках в нуль одновременно.
Восстановление изображения в пространственной области достигается применением обратного преобразования Фурье к оценке 
. Отметим, что если шум равен нулю, то и его энергетический спектр обращается в нуль, и в этом случае винеровская фильтрация сводится к инверсной фильтрации.
В том случае, если на изображении присутствует белый шум, спектр которого 
является постоянной функцией, то выражение для винеровского фильтра упрощается. Однако, в большинстве случаев спектр неискаженного изображения редко бывает известен. В тех случаях, когда спектры шума и неискаженного изображения неизвестны и не могут быть оценены, часто используется подход, состоящий в аппроксимации исходного выражения следующим выражением:
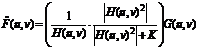
где K – определенная константа.
Винеровская фильтрация обладает несомненным преимуществом по сравнению с инверсной фильтрацией, и позволяет получить результаты восстановления изображения очень близкие по виду к исходному изображению.
Среднегеометрический фильтр
Обобщением винеровского фильтра является среднегеометрический фильтр, определяемый следующим выражением:
где: α и β – положительные вещественные константы.
При α=1 среднегеометрический фильтр сводится к инверсному фильтру, при α=0 фильтр превращается в параметрический винеровский фильтр, который при β=1 сводится в свою очередь к обычному винеровскому фильтру. При α=0,5 фильтр представляет собой среднегеометрическое двух величин, откуда и происходит название самого фильтра. При α=0,5 и β=1 фильтр известен как фильтр эквализации спектра.
Таким образом, представленный среднегеометрический фильтр является обобщенной моделью для целого семейства различных фильтров, использующихся при восстановлении изображений от присутствующих на них шумов и помех.
5.7 Фильтрация методом минимизации сглаживающего функционала со связью
Большинству методов восстановления присуща общая проблема, заключающаяся в необходимости иметь некоторую информацию относительно искажающей функции. Применением винеровской фильтрации связано с дополнительной трудностью, состоящей в том, что энергетические спектры неискаженного изображения и шума должны быть известны.
Существуют методы, требующие наличие информации исключительно о среднем значении и дисперсии шума. Одним из таких методов является фильтрация методом минимизации сглаживающего функционала со связью. Данный метод обладает особенным свойством, заключающимся в том, что с его помощью можно получить оптимальный результат для каждого конкретного изображения, к которому он применяется.
Используя определение свертки, запишем в матрично-векторном виде выражение, определяющее матрицу искаженного изображения G:
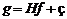
Пусть искаженное изображение g (x, y) имеет размеры M × N. Тогда можно сформировать вектор g таким образом, чтобы первые N его элементов были равны значениям в первой строке изображения g (x, y), следующие N элементов были равны значениям во второй строке и т.д. Полученный вектор будет иметь размер M· N. Аналогично формируются векторы f и ç, которые в результате имеют те же размеры. Матрица H – матрица искажающего оператораимеет размеры M· N × M· N, а ее элементы задаются значениями h в свертке.
Основной проблемой восстановления является высокая чувствительность матрицы искажающего оператора H к шуму. Один из способов преодоления трудности состоит в регуляризации поставленной задачи, которая достигается заменой исходной задачи на задачу нахождения экстремума (минимума) некоторого сглаживающего функционала. В качестве такого функционала C [ f ] можно использовать квадрат нормы лапласиана:
с дополнительным ограничением (связью) вида:
где: 
– искомая оценка неискаженного изображения, 
– евклидова норма вектора w, определяемая как: 
, wk – k -ая координата вектора.
Решение данной оптимизационной задачи в частотной области определяется выражением следующего вида:
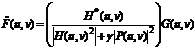
где: параметр γ (параметр регуляризации) выбирается таким образом, чтобы выполнялось приведенное выше ограничение о равенстве квадратов норм; функция P(u, v) определяется Фурье-преобразованием функции вида (т.е. маска оператора Лапласа):
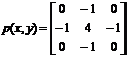
Фильтрация методом минимизации сглаживающего функционала обеспечивает сопоставимые по качеству результаты с винеровской фильтрации, однако, не требует, априорной информации об энергетических спектрах неискаженного изображения и шума.
5.8 Геометрические преобразования
Геометрические преобразования также могут успешно применяться при решении задач восстановления изображений. Суть геометрических преобразований сводится к изменению пространственных взаимосвязей между пикселями на изображении. С точки зрения цифровой обработки изображений геометрические преобразования состоят из следующих двух основных операций:
1) пространственное преобразование, в результате которого происходит изменение расположения точек изображения в плоскости;
2) интерполяция значений яркости, при которой происходит присвоение значений яркости точкам изображения, подвергнутого пространственному преобразованию.
Пространственные преобразования
Предположим, что изображение f с координатами пикселей (x, y) подвергается геометрической деформации, в результате чего формируется изображение g с координатами (x ̸
