4.1 Предварительные замечания. Введение в Фурье-анализ
Частотные методы улучшения изображений основаны на выполнении преобразования Фурье над функцией двух переменных (над функцией дискретного изображения). Прямое дискретное Фурье-преобразование функции f(x, y), изображения размером M×N задается равенством:
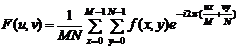
где: u=0,1,2,…, M–1; v=0,1,2,…, N–1
Обратное преобразование Фурье задается выражением:

Переменные u и v называются переменными преобразования или частотными переменными, а переменные x и y называются пространственными переменными или переменными изображения. Как правило, числа M и N являются четными для упрощения компьютерной реализации, а центр Фурье образа находится в точке с координатами: u=(M/2)+1, v=(N/2)+1. Значение Фурье-преобразования в точке (u, v)=(0, 0) равно:

Таким образом, если f(x, y) – изображение, то значение Фурье-преобразования в начале координат равно среднему значению яркости на изображении. Поскольку началу координат отвечают нулевые частоты, то величину F(0, 0) часто называют постоянной составляющей спектра. В силу того, что функция f(x, y) вещественная, то спектр Фурье-преобразования изображения обладает свойством симметрии. Справедливы следующие соотношения между отсчетами в пространственной и частотной области:

Центрированный спектр простой двумерной функции
Необходимо отметить, что Фурье-спектр состоит из пикселей, имеющих большой динамический диапазон. Система воспроизведения изображений, как правило, не способна правильно отобразить столь большой диапазон значений интенсивности, что приводит к тому, что при обычном отображении спектра Фурье теряется значительное число деталей. В этой связи для улучшения зрительного восприятия полутонов, изображение спектра подвергается логарифмическому преобразованию.
На рисунке 25 слева представлен белый прямоугольник размерами 20×40 пикселей, наложенный на черный фон размерами 512×512 пикселей, на рисунке 25 справа представлен центрированный Фурье спектр изображения. Для того, чтобы центрировать спектр необходимо исходное изображение умножить на (-1)x+yперед вычислением Фурье-преобразования.

Рисунок 25 – Слева – изображение белого прямоугольника размерами 20×40 пикселей на черном фоне размерами 512×512 пикселей, справа – центрированный Фурье-спектр, представленный после применения логарифмического преобразования
Фильтрация в частотной области
Частотная область цифрового изображения представляет собой не что иное, как пространство, в котором принимают значения переменные (u, v) Фурье-преобразования. Как известно частота сигнала прямо связана со скоростью изменения сигнала, поэтому интуитивно понятно, что частоты в Фурье-преобразовании связаны с вариацией яркости на изображении. Наиболее медленно меняющаяся (постоянная) частотная составляющая (u=0, v=0) совпадает со средней яркостью изображения. Низкие частоты, соответствующие точкам вблизи начала координат Фурье-преобразования, определяют медленно меняющиеся компоненты изображения. По мере удаления от начала координат, более высокие частоты начинают соответствовать все более и более быстрым изменениям яркости, представляющие собой границы объектов и другие детали изображения, характеризующиеся резкими изменениями яркости, например шум на изображении.
Основы фильтрации в частотной области
Процедура фильтрации в частотной области просто и состоит из следующих шагов:
1. Исходное изображение умножается на (–1)x+y, чтобы его Фурье преобразование оказалось центрированным.
2. Вычисляется прямое дискретное преобразование Фурье (ДПФ) F(u, v) исходного изображения.
3. Функция F(u, v) умножается на функцию фильтра H(u, v).
4. Вычисляется обратное ДПФ от результата шага 3.
5. Выделяется вещественная часть результата шага 4.
6. Результат шага 5 умножается на (–1)x+y.
Функция фильтра H(u, v) или передаточная характеристика фильтра подавляет некоторые частоты преобразования, оставляя другие при этом без изменения. На рисунке 26 представлена структурная схема, включающая основные этапы проведения фильтрации изображения в частотной области.

Рисунок 26 – Основные этапы фильтрации изображения в частотной области
На стадии предварительной обработки помимо умножения изображения на (–1)x+y, могут применяться операции яркостного масштабирования, нормировка размеров исходного изображения, преобразование формата входных данных в формат с плавающей точкой и ряд других.
Некоторые основные фильтры и их свойства
Основными видами используемых фильтров являются: низкочастотный фильтр – ослабляет высокие частоты, одновременно, пропуская низкие частоты; высокочастотный фильтр – фильтр, обладающий противоположными свойствами. Низкие частоты Фурье-преобразования отвечают за возникновение превалирующих значений яркости на гладких участках изображения, в то время как высокие частоты отвечают преимущественно за контуры и шум. После применения низкочастотной фильтрации изображение, по сравнению с исходным изображением, содержит меньше резких деталей. После применения высокочастотной фильтрации на изображении уменьшаются изменения яркости в пределах больших гладких областей и выделяются переходные зоны быстрого изменения яркости, то есть контуры изображения, как правило, такое изображение обладает большей резкостью по сравнению с исходным.
В силу того, что высокочастотные фильтры почти полностью подавляют постоянную составляющую F(0, 0), которая определяет среднюю яркость изображения, выходное изображения после обработки таким фильтром выглядит очень темным, для устранения указанного недостатка к передаточной функции фильтра добавляют константу, равную половине высоты фильтра.
Другим видом частотного фильтра является фильтр-пробка или режекторный фильтр, вырезающий определенное значения яркости из изображения, как правило, это значение яркости в точке начала координат – среднее значение яркости изображения. Необходимо заметить, что среднее значения яркости не может быть строго равно нулю, поскольку для этого некоторые элементы изображения должны содержать отрицательные значения, а средства отображения графической информации не могут оперировать с отрицательными значениям яркости. Для устранения указанного противоречия наименьшее отрицательное значение приравнивают к нулю (уровень черного), а остальные значения пропорционально увеличивают.
Соответствие между фильтрацией в пространственной области и фильтрацией в частотной области
Взаимосвязь между пространственной и частотной областями фильтрации устанавливается с помощью теоремы о свертке. В основе операции свертки лежит процедура смещения некоторой маски по изображению от элемента к элементу и вычисление для каждого такого элемента некоторой заранее определенной величины. Дискретная свертка двух функций f(x, y) и h(x, y) размерами M×N обозначается символом f(x, y)*h(x, y) и определяется выражением:

Если F(u, v) и H(u, v) обозначают соответственно Фурье образы функций f(x, y) и h(x, y), то теорема о свертке утверждает, что функции f(x, y)*h(x, y) и F(u, v)·H(u, v) образуют Фурье-пару, утверждение может быть формально записано в виде:
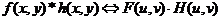
Справедливо также и обратное утверждение: свертка в частотной области приводит к умножению в пространственной области:
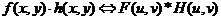
Ведем понятие импульсная функция (или дельта-функция) интенсивностью А, локализованная в точке с координатами (x0, y0), для которой будем использовать обозначение А ·δ(x – x0, y – y 0), определяется выражением:
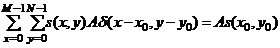
Таким образом, суммирование любой функции s(x, y), умноженной на импульс, дает значение этой функции в точке локализации импульса, умноженное на амплитуду импульса. Импульсная функция А ·δ(x – x0, y – y 0) является изображением размера M×N, состоит из нулей за исключением точки с координатами (x0, y0), в которой значение изображения равно А. Импульсная функция обладает свойством отсеивания, в силу того, что свертка импульсной функцией с функцией изображения “копирует” значение функции изображения в точке локализации импульсной функции.
Вычислим Фурье-образ единичного импульса (А =1) в начале координат (u=0, v=0):

Фурье-образ единичного импульса в начале координат пространственной области представляет собой постоянную вещественную функцию. Вычислим свертку единичного импульса с функцией изображения h(x, y):

На основе теоремы о свертке можем получить следующие выражения:
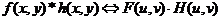
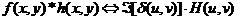

Таким образом, очевидно, что фильтры в пространственной и частотной областях образуют Фурье-пару. В силу этого, по заданному в частотной области фильтру мы можем получить соответствующий фильтр в пространственной области, применив к первому обратное преобразование Фурье.
Фильтры на основе гауссовой функции
Данный тип фильтров обладает двумя важными свойствами:
1) прямое и обратное Фурье-преобразования гауссовой функции также являются гауссовыми функциями;
2) форма такого фильтра задается всего двумя параметрами.
Ограничимся рассмотрением одномерного случая. Пусть H(u) – частотная передаточная функция гауссова фильтра, которая задается равенством:

где: σ – гауссово среднеквадратичное отклонение.
Соответствующий фильтр в пространственной области задается равенством:

Данные выражения наглядно показывают, что если функция H(u) имеет широкий профиль (большое значение σ), то функция h(x) имеет узкий профиль и наоборот. График гауссова фильтра в частотной области показан на рисунке 27 А.

Рисунок 27 – А – низкочастотный гауссов фильтр в частотной области, Б – соответствующий низкочастотный фильтр в пространственной области, В – высокочастотный гауссов фильтр в частотной области, Г – соответствующий высокочастотный фильтр в пространственной области
Анализируя форму данного фильтра, становится очевидно, что это низкочастотный фильтр. Соответствующий фильтр в пространственной области представлен на рисунке 27 Б, все значения данного фильтра являются положительными числами, это означает, что низкочастотная фильтрация в пространственной области может быть осуществлена при помощи маски, целиком состоящей из положительных коэффициентов. Также необходимо отметить, что чем более узким в частотной области является фильтр, тем сильнее он подавляет высокие частоты, что выражается в дальнейшей расфокусировки изображения. Это эквивалентно использованию более широкого фильтра в пространственной области.
На основе гауссовых функций можно построить более сложные фильтры, например, высокочастотный фильтр может быть задан с помощью двух гауссовых функций:

где: A≥B и σ1≥σ2.
Соответствующий фильтр в пространственной области имеет вид:

Маска пространственного высокочастотного фильтра содержит отрицательные коэффициенты в отличие от низкочастотного фильтра. Для высокочастотного фильтра также справедливым является взаимообратное отношение ширины профилей.
К преимуществам фильтров в частотной области по сравнению с фильтрами в пространственной области относятся:
1) большая эффективность вычисления при одинаковом размере фильтров, особенно при использовании алгоритмов быстрого преобразования Фурье;
2) фильтрация в частотной области является боле наглядной, поэтому зачастую позволяет получить тривиальное решение тех задач, прямое решение которых представляет собой сложную или невозможную реализацию в пространственной области.
Однако, необходимо заметить, что целый ряд наиболее распространенных проблем в области обработки изображения можно реализовать методами пространственной фильтрации с использованием масок относительного малого размера, что позволяет достичь заметного выигрыша в быстродействии.
4.2 Сглаживающие частотные фильтры
Как отмечалось ранее, контуры и другие резкие перепады яркости на изображении, включая шумы, вносят значительный вклад в высокочастотные составляющие его Фурье-преобразования. Сглаживание изображения в частотной области достигается путем ослабления высокочастотных компонент определенного диапазона Фурье-образа данного изображения.
Модель фильтрации изображения в частотной области в обобщенном виде может быть описана следующим равенством:
G(u, v)= H(u, v)· F(u, v)
где: F(u, v) – Фурье-образ изображения, которое подлежит операции фильтрации, H(u, v)· - передаточная функция фильтра, которая ослабит высокочастотные компоненты F(u, v) и сформирует функцию G(u, v).
Рассмотрим три вида низкочастотных фильтров: идеальный фильтр, фильтр Баттерворта и гауссов фильтр. Указанные фильтры по виду передаточной функции покрывают диапазон от очень резких фильтров (идеальный фильтр) до очень гладких фильтров (гауссов фильтр).
Фильтр Баттерворта является единственным из рассматриваемых, который характеризуется порядком фильтра – параметром, определяющим крутизну передаточной функции фильтра. При малых значениях порядка фильтра передаточная функция имеет гладкую форму, близкую по форме к передаточной характеристике гауссова фильтра; при высоких значениях фильтр характеризуется крутой передаточной функцией и приближается по форме к характеристик идеального фильтра.
Идеальные фильтры низких частот
Идеальный фильтр низких частот представляют собой такой низкочастотный фильтр, который обрезает все высокочастотные составляющие Фурье-образа, находящиеся на большем расстоянии от начала координат центрированного изображения, чем некоторое заданное расстояние D0. Такой тип фильтра еще называется двумерным идеальным низкочастотным фильтром и имеет передаточную функцию:

где D0 – заданная неотрицательная величина, точка профиля фильтра, в которой совершается переход от значений H(u, v) =1 к значениям H(u, v) =0, называемая частотой среза; D(u, v) – расстояние от точки (u, v) до начала координат – центра частотного прямоугольника. В силу того, что Фурье-преобразование центрировано, расстояние D(u, v) определяется по формуле:

На рисунке 28 представлен идеальный низкочастотной фильтр в виде изображения, а также радиальный профиль фильтра:

Рисунок 28 – слева: представление идеального низкочастотного фильтра в виде изображения, справа: радиальный профиль фильтра
Идеальность фильтра подчеркивается тем, что все частоты внутри круга радиуса D0 проходят без изменения, в то время как частоты вне круга подавляются полностью. Низкочастотный идеальный фильтр обладает свойством симметрии относительно начала координат, поэтому для того, чтобы однозначно задать фильтр достаточно построить один радиальный профиль – функция расстояния от начала координат. Передаточная функция фильтра в координатах H(u, v) получается вращением профиля на 3600 вокруг начал координат.
Одним из способов выбора эталонного набора положений частот среза состоит в том, чтобы определить круги, в которых заключена заданная часть полной энергии изображения PT. Полная энергия будет определена как сумма компонент энергетического спектра во всех точках (u, v); u =0, 1, 1… M –1; v =0, 1, 1… N –1.

где величина P(u, v) определяется как:
P(u, v)=| F(u, v)|2
где F(u, v) – Фурье-преобразование исходного изображения f(x, y).
Частота r (α) определятся как радиус круга с центром в центре частотного прямоугольника, содержащего α процентов энергии спектра изображения, т.е.:
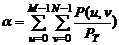
Выбор неоптимального значения частоты среза фильтра может привести к значительным искажениям обрабатываемого изображения: выбор слишком малого значения частоты среза приведет к устранению большинства деталей изображения. В то время как выбор относительно большого значения частоты среза приведет к тому, что выходное изображение будет незначительно отличаться от исходного, при этом уровень шума также не изменится.
При использовании идеального фильтра низких частот возникают нежелательные эффекты, такие как эффекты размывания и появления ложных контуров, при этом при уменьшении ширины используемого фильтра в частотной области эффекты размытия изображений усиливаются.
Возникающие нежелательные эффекты при использовании идеального фильтра низких частот получили название “звон” (или эффект Гиббса), выражающийся в появлении ложных контуров вокруг реальных контуров. Структура ложных контуров становится тоньше по мере уменьшения энергии отсекаемой высокочастотной составляющей.
Природа появления ложных контуров может быть объяснена при помощи теоремы о свертке, согласно которой, существует пространственный аналог идеального фильтра низких частот. Пространственная функция такого фильтра может быть определена с помощью обратного преобразования Фурье от передаточной функции низкочастотного фильтра и представляет собой последовательность круговых концентрических колец различной яркости, приводящих главным образом к появлению ложных контуров: рисунок 29 иллюстрирует проявление эффекта Гиббса при использовании идеального фильтра низких частот.
Под понятием профиль яркости подразумевается зависимость изменения яркости пикселей от номера пикселей, расположенных на горизонтальной прямой, как правило, проходящей через центр изображения; отсчет пикселей по прямой начинается с крайне левого пикселя и заканчивается крайне правым пикселем.

Рисунок 29 – А – изображение идеального фильтра низких частот, Б – профиль яркости в пространственной области, В – изображение идеального низкочастотного фильтра в пространственной области, Г – условное изображение, состоящее из 5 ярких точек в пространственной области, Д – свертка изображений В и Г, Е – профиль яркости отфильтрованного изображения Д
Таким образом, приведенные результаты фильтрации с помощью идеального низкочастотного фильтра показывают, что идеальные фильтры низких частот не имеют большого практического применения.
Фильтры низких частот Баттерворта
Передаточная функция низкочастотного фильтра Баттерворта порядка n с частотой среза на расстоянии D0 от начала координат задается формулой:

Радиальные профили передаточной функции низкочастотного фильтра Баттерворта в зависимости от порядка фильтра представлены на рисунке 30.
В отличие от идеального низкочастотного фильтра передаточная функция низкочастотного фильтра Баттерворта не имеет разрыва, который устанавливает точную границу между пропускаемыми и обрезаемыми частотами.
К преимуществам низкочастотных фильтров Баттерворта относится намного меньшее проявление нежелательных эффектов размытия и появления ложных контуров, по сравнению с идеальными низкочастотными фильтрами. С увеличением порядка низкочастотного фильтра Баттерворта возрастает проявление эффектов размытия, принято считать, что низкочастотный фильтр Баттерворта второго порядка является оптимальным с точки зрения компромисса между эффективностью низкочастотной фильтрации и приемлемым уровнем проявления ложных контуров и общего размытия изображения.

Рисунок 30 – Радиальные профили передаточной функции низкочастотного фильтра Баттерворта в зависимости от порядка фильтра
На рисунке 31 приведены профили яркости изображений низкочастотных фильтров Баттерворта с одинаковой частотой среза порядка 1, 2, 5 и 20 соответственно.

Рисунок 31 – слева направо: профили яркости низкочастотных фильтров
Баттерворта с одинаковой частотой среза порядка 1, 2, 5 и 20 соответственно
Гауссовы фильтры низких частот
В двумерном случае гауссовы фильтры низких частот задаются формулой:

где σ задает ширину гауссовой кривой, обозначив σ= D 0, (D 0 – частота среза фильтра) перепишем выражение для фильтра в виде:

При величине D(u, v) = D 0, значение передаточной функции фильтра составляет 0,667 от своего максимального значения. На рисунке 32 приведены радиальные профили гауссова фильтра при различных значениях D 0.
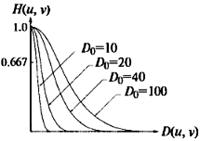
Рисунок 32 – Радиальные профили передаточной функции низкочастотного гауссова фильтра при различных значениях частоты среза D 0
Как было показано ранее, обратное преобразование Фурье от гауссовой функции является также гауссовой функцией. Иными словами, данное свойство гауссовой функции означает, что пространственный гауссов фильтр низких частот, полученный с помощью обратного преобразования Фурье от передаточной функции частотного гауссова фильтра, будет положительным, и не будет иметь концентрических колец. Это приведет к полному отсутствию звона на обрабатываемом изображении, что является основным преимуществом гауссовых низкочастотных фильтров по сравнению с фильтрами Баттерворта. Тем не менее, применение низкочастотного гауссова фильтра обеспечивает зачастую меньшее сглаживание при одинаковой частоте среза по сравнению с фильтрами Баттерворта, поэтому в тех случаях, когда требуется жесткий контроль переходной зоны от низких частот к высоким частотам, фильтры Баттерворта представляются более подходящим выбором. В задачах обработки биомедицинских изображений отсутствие ложных контуров и недопустимость проявления артефактов любого рода предпочтительным является использование гауссовых фильтров.
4.3 Частотные фильтры повышения резкости
Контуры и другие скачкообразные изменения яркости на изображении связаны с высокочастотными составляющими Фурье-преобразования изображения. Повышение резкости изображения может быть достигнуто в частотной области при помощи процедуры высокочастотной фильтрации, которая подавляет низкочастотные составляющие и не затрагивает высокочастотную часть Фурье-преобразования.
Передаточная функция высокочастотных фильтров может быть получена при помощи следующего соотношения:
Hhp(u, v) =1− Hlp(u, v)
где: Hlp(u, v) – передаточная функция соответствующего низкочастотного фильтра.
Рассмотрим следующие виды высокочастотных фильтров: идеальные высокочастотные фильтры, высокочастотные фильтры Баттерворта и гауссовы высокочастотные фильтры. Для изучения свойств высокочастотных фильтров в пространственной области необходимо, как и ранее для случая низкочастотных фильтров, выполнить следующие операции: (1) умножить функцию фильтра H(u, v) на (−1) u+ v для центрирования; (2) вычислить обратное ДПФ; (3) умножить действительную часть обратного ДПФ на (−1) x+ y.
Идеальные фильтры высоких частот
Двумерные идеальные высокочастотные фильтры определяются формулой:

где D0 – частота среза, равная расстоянию от центра частотного прямоугольника, D(u, v) – расстояние от точки с координатами (u, v) до центра частотного прямоугольника (начала координат).
На рисунке 33 приведен радиальный профиль передаточной функции идеального высокочастотного фильтра.

Рисунок 33 – Радиальный профиль передаточной функции идеального
высокочастотного фильтра
Идеальным высокочастотным фильтрам, точно также как и идеальным низкочастотным фильтра, присущ эффект Гиббса, который приводит к появлению “звона” на обрабатываемом изображении. На рисунке 34 приведена функция идеального высокочастотного фильтра в пространственной области и соответствующий профиль яркости.

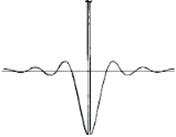
Рисунок 34 – Слева: функция идеального высокочастотного фильтра в пространственной области, справа: соответствующий профиль яркости
По аналогии с идеальными низкочастотными фильтрами идеальные высокочастотные фильтры также почти не имеют реального практического применения.
Фильтры высоких частот Баттерворта
Передаточная функция высокочастотного фильтра Баттерворта порядка n с частотой среза на расстоянии D0 от начала координат определяется выражением:
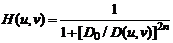
На рисунке 35 приведены радиальный профиль передаточной функции высокочастотного фильтра Баттерворта второго порядка, функция высокочастотного фильтра Баттерворта в пространственной области, а также профиль яркости пространственной функции фильтра.
Фильтры Баттерворта высоких частот приводят к гораздо меньшим искажениям границ объектов, чем идеальные высокочастотные фильтры Баттерворта. С увеличением порядка высокочастотного фильтра Баттерворта искажения границ объектов заметно увеличиваются.


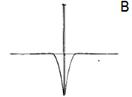
Рисунок 35 – А – радиальный профиль передаточной функции высокочастотного фильтра Баттерворта второго порядка, Б – функция высокочастотного фильтра Баттерворта в пространственной области, В – профиль яркости пространственной функции фильтра
Гауссовы фильтры высоких частот
Передаточная функция гауссова фильтра высоких частот с частотой среза, расположенной на расстоянии D0 от начала координат, задается выражением:

На рисунке 36 приведены: радиальный профиль передаточной функции гауссова фильтра высоких частот, функция высокочастотного гауссова фильтра в пространственной области, а также профиль яркости пространственной функции гауссова фильтра.
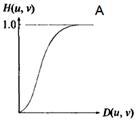


Рисунок 36 – А – радиальный профиль передаточной функции высокочастотного гауссова фильтра, Б – функция высокочастотного гауссова фильтра Баттерворта в пространственной области, В – профиль яркости пространственной функции фильтра
Высокочастотный гауссов фильтр обеспечивает высокое качество фильтрации даже для маленьких объектов и тонких полос, характеризуется полным отсутствием искажений.
Лапласиан в частотной области
Фильтры, определенные в пространственной области, могут быть также описаны в частотной области, путем выполнения преобразования Фурье над пространственной функцией фильтра.
Одним из свойств прямого преобразования Фурье является следующее:

На основании данного выражения можем записать следующее равенство:

 Выражение в левой части равенства представляет собой лапласиан функции f(x, y). Таким образом, имеет место следующее равенство:
Выражение в левой части равенства представляет собой лапласиан функции f(x, y). Таким образом, имеет место следующее равенство:

Последнее выражение показывает, что вычисление лапласиана можно осуществить в частотной области с помощью фильтра следующего вида:
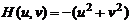
Начало координат для функции F(u, v) находится в центре частотного прямоугольника, что достигается умножением функции f(x, y) на (-1) x+ y перед вычислением ее Фурье-преобразования. Если функция изображения f(x, y) имеет размеры M× N, то в результате такого умножения центр преобразования попадает в точку (M/2, N/2) частотного прямоугольника. Центр передаточной функции фильтра также должен быть сдвинут:
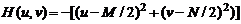
Результат применения дискретного оператора Лапласа, заданного в частотной области, получается, посредством вычисления обратного преобразования Фурье от функции H(u, v)· F(u, v):

На рисунке 37 представлено трехмерное изображение передаточной функции лапласиана в частотной области H(u, v), двумерное полутоновое изображение лапласиана в частотной области, изображение лапласиана в пространственной области и соответствующий профиль яркости, а также маска лапласиана.
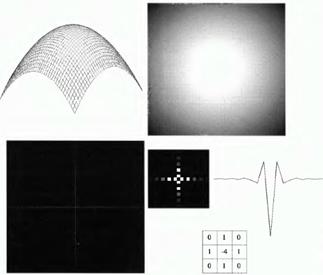
Рисунок 37 – А – трехмерное изображение лапласиана в частотной области, Б – двумерное полутоновое изображение лапласиана в частотной области, В – изображение лапласиана в пространственной области, Г – увеличенный центральный фрагмент изображения В, Д – профиль яркости пространственной функции лапласиана, Е – маска лапласиана
Для получения улучшенного изображения g(x, y) необходимо из исходного изображения f(x, y) вычесть лапласиан-изображение, полученное с использованием частотного фильтра Лапласа:
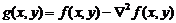
Обработку в частотной области можно полностью осуществить, используя один фильтр, передаточная характеристика которого определяется следующим образом:
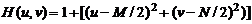
Для получения корректного результата необходимо осуществить масштабирование фильтра, поскольку квадраты переменных могут быть больше единицы на несколько порядков. Применение лапласиана приводит к увеличению резкости мелких деталей на обрабатываемом изображении.
Нерезкое маскирование. Высокочастотная фильтрация с подъемом
частотной характеристики
Изображения, получаемые в результате высокочастотной фильтрации, имеют среднее значение яркости фона близкое к нулю, так как высокочастотные фильтры, применяемые для обработки данных изображений, уничтожают постоянную составляющую (нулевую компоненту) их Фурье-преобразования. Для устранения данного недостатка можно к результату фильтрации добавить некоторую долю исходного изображения в качестве, так называемой “подложки изображения”. В ряде случаев представляется необходимым увеличить вклад, привносимый исходным изображением в итоговый результат фильтрации. Такой подход называется методом высокочастотной фильтрации с подъемом частотной характеристики и представляет собой обобщение метода нерезкого маскирования.
Нерезкое маскирование состоит в формировании резкого изображения путем вычитания из оригинала его сглаженной копии. В терминах частотных преобразований это означает, что имеет место высокочастотная фильтрация, которая достигается вычитанием из исходного изображения f(x, y) результата его низкочастотной фильтрации flp(x, y):
fhp(x, y)=f(x, y)−flp(x, y)
Обобщением последнего выражения является следующее выражение, описывающее высокочастотную фильтрацию с подъемом частотной характеристики:
fhb(x, y)=A·f(x, y)−flp(x, y)
Фильтрация с подъемом частотной характеристики позволяет изменять вклад, вносимый исходным изображением в конечный результат обработки. Запишем последнее выражение в следующем виде:
fhb(x, y)=(A−1)· f(x, y)+ f(x, y)− flp(x, y) или: fhb(x, y)=(A−1)· f(x, y)+ fhp(x, y)
Последнее выражение показывает, что основу метода фильтрации составляет высокочастотная, а не низкочастотная фильтрация. При A =0, фильтрация с подъемом частотной характеристики сводится к обычной высокочастотной фильтрации, если значение А превышает 1, то вклад исходного изображения становится более заметным.
Учитывая, что Fhp(u, v) = F(u, v)− Flp(u, v) и Flp(u, v)= Hlp(u, v)· F(u, v), где Hlp(u, v) – передаточная функция низкочастотного фильтра, то нерезкое маскирование может быть осуществлено непосредственно в частотной области с использованием составного фильтра вида:
Hhp(u, v) =1− Hlp(u, v)
Аналогично фильтрация с подъемом частотной характеристики может быть осуществлена при помощи следующего составного частотного фильтра:
Hhb(u, v) =(A −1)+ Hhp(u, v), при A ≥1
Процедура включает умножение фильтра на центрированное изображение Фурье-преобразования входного изображения и затем вычисления обратного преобразования Фурье от произведения. Умножение действительной части полученного результата на (−1) x+ y дает изображение в пространственной области, являющееся результатом фильтрации с подъемом частотной характеристики.
Фильтрация с усилением высоких частот
Иногда при обработке изображения выгодно усилить его высокочастотную составляющую. Передаточная функция фильтра с усилением высоких частот задается выражением:
Hhfe(u, v) = a + bHhp(u, v)
Характерные значения а находятся в диапазоне от 0,25 до 0,5; характерные значения b – в диапазоне от 1,5 до 2,5 (при этом важно отметить, что b > a). При значениях b >1 происходит усиление высоких частот, откуда и происходит название метода.
Основная сфера применения фильтрации с усилением высоких частот в задачах обработки биомедицинских изображений является повышение резкости рентгенографических изображений. Рентгеновские лучи не могут быть сфокусированы с помощью линз, как световые лучи, поэтому большинство рентгеновских снимков выглядят расплывчато. Зачастую яркость рентгенографических изображений сдвинута в темную область, поэтому также необходимо использовать методы обработки изображения для увеличения яркости контрастности изображения.
На рисунке 38 А представлен рентгеновский снимок грудной клетки с узким диапазоном изменения яркости. На рисунке 38 Б представлен результат высокочастотной фильтрации исходного изображения с использованием фильтра Баттерворта порядка 2 с частотой среза D0, равной 5% вертикального размера изображения. Полученное после фильтрации изображение маловыразительно, сложно отличить даже основные контуры оригинального изображения. Изображение, приведенное на рисунке 38 В демонстрирует преимущества фильтрации с усилением частот (в данном случае использовались следующие параметры: a =0.5 и b =2). На рисунке 38 Г приведен результат обработки изображения В, характеризующегося узким диапазоном яркости, с помощью метода эквализации гистограммы.
Таким образом, итоговый результат, полученный при использовании фильтрации с усилением высоких частот и эквализации гистограммы, приводит к большему результату по сравнению с использованием каждого метода по отдельности, Комплексное использование различных процедур и методов улучшения изображения является отличительной особенностью при решении целого ряда задач обработки биомедицинских изображений.

Рисунок 38 – А – рентгеновский снимок грудной клетки, Б – результат высокочастотной фильтрации с использованием фильтра Баттерворта, В – результат фильтрации с усилением высоких частот, Г – результат применения метода эквализации гистограммы к изображению В
4.4 Гомоморфная фильтрация
Изображение f(x, y) согласно предложенной ранее математической модели может быть представлено в виде произведения освещенности и коэффициента отражения:
f(x, y) = i(x, y)· r(x, y)
Рассмотрим следующую величину:
z(x, y) = lnf(x, y) = ln[i(x, y)] + ln[r(x, y)]
Необходимо с осторожностью подходить к логарифмированию изображения, в силу того, что некоторые элементы изображения могут обратиться в нуль.
Перейдем в пространство Фурье-преобразования и запишем:
Z(u, v) = Fi(u, v) + Fr(u, v)
где: Fi(u, v) – Фурье-образфункции ln[i(x, y)], Fr(u, v) – Фурье-образфункции ln[r(x, y)].
Подвергнем функцию Z(u, v) процедуре фильтрации с помощью фильтра H(u, v). Тогда можем записать следующее выражение:
S(u, v) = H(u, v)· Z(u, v)= H(u, v)· Fi(u, v) + H(u, v)· Fr(u, v)
где: S(u, v) – Фурье-образ результата.
В пространственной области соответственно запишем:

Если обозначить:
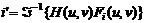

В этом случае результат фильтрации в пространственной области можно записать в виде:
s(x, y) = i′(x, y)+ r′(x, y)
В силу того, что функция z(x, y) была получена в результате логарифмирования исходного изображения f(x, y), то обратная операция – потенцирование позволяет получить искомое обработанное изображение, обозначаемое g(x, y):
g(x, y) = es(x, y) = ei′(x, y)·er′(x, y) = i0(x, y)·r0(x, y)
где: i0(x, y) – освещенность исходного изображения, r0(x, y) – коэффициент отражения исходного изображения.
Метод обработки изображения, основанный на использовании представленного метода, схематически представлен на рисунке 39.

Рисунок 39 – Структурная схема метода гомоморфной фильтрации для обработки изображений
Ключевым моментом рассматриваемого подхода является разложение изображения на составляющие, связанные с освещенностью и коэффициентом отражения. Гомоморфный фильтр с передаточной функцией H(u, v) применяется к каждой из полученных составляющих по отдельности.
Составляющие изображения, связанные с освещенностью, обычно характеризуется медленными изменениями в пространственной области, в то время как составляющая, обусловленная коэффициентом отражения, характеризуется резкими изменениями, особенно в местах соединения разнородных объектов. Данные различия позволяют ассоциировать низкочастотную составляющую преобразования Фурье от логарифма изображения с освещенностью, а высокочастотную – с коэффициентом отражения.
Использование гомоморфного фильтра предоставляет возможность в значительной степени контролировать каждую из составляющих. Для этого необходимо задать передаточную функцию H(u, v) так, чтобы фильтр по-разному действовал на низкочастотные и высокочастотные составляющие Фурье-преобразования. На рисунке 40 представлен радиальный профиль гомоморфного фильтра.

Рисунок 40 – Радиальный профиль передаточной функции гомоморфного фильтра
В том случае, если параметры фильтра γL и γH выбраны так, что γL<1 и γH>1, то гомоморфный фильтр в данном случае будет ослаблять вклад, вносимый низкими частотами (освещенностью) и усиливать вклад, вносимый высокими частотами (коэффициентом отражения). Конечный результат воздействия гомоморфным фильтром заключается в одновременном сжатии динамического диапазона и усилении контраста.
Для аппроксимации кривой, показанной на рисунке 40, можно использовать любые из основных видов высокочастотных фильтров, рассмотренных ранее. Например, использование модифицированного гауссова высокочастотного фильтра с передаточной характеристикой вида:

В данном выражении константа с введена для того, чтобы контролировать крутизну наклона передаточной функции фильтра в переходной области между γL и γH.






