Изображений
3.1 Градационные преобразования
Под методами улучшения изображения подразумевается осуществления таких преобразований над исходным изображением, которое приводит к получению результата более подходящего с точки зрения конкретного применения. Визуальное оценивание качества изображения представляет собой крайне субъективный процесс. В том случае, когда целью обработки изображения является их дальнейшее использование в системах машинного восприятия, критерием эффективности обработки исходного изображения является получение более точных результатов машинного распознавания.
Множество подходов к улучшению изображения распадается на 2 категории: методы обработки в пространственной области и методы обработки в частотной области. Термин пространственная область относится к плоскости изображения как таковой, и данная категория объединяет подходы, основанные на прямом манипулировании пикселями изображения.
Пространственные методы представляют собой процедуры, оперирующие непосредственно значениями пикселей и описываются уравнением:

где: f(x, y) – входное изображение, g(x, y) – обработанное изображение, T – оператор над f, определенный в некоторой окрестности точки (x, y). Под окрестностью точки понимается квадратная или прямоугольная область, являющаяся подмножеством изображения и центрированная относительно данной точки.

Рисунок 9 – Градационное преобразование для улучшения контраста
Простейшая форма оператора T достигается в случае, когда окрестность имеет размер в один пиксель, в этом случае значение g зависит только от значения f в точке (x, y) и T становится функцией градационного преобразования. Оператор T часто называют также функцией преобразования интенсивностей или функцией отображения и записывают в виде: s=T(r). Переменные r и s представляют собой значения яркостей изображений f(x, y) и g(x, y) в точке (x, y). Если T(r) имеет вид как на рисунке 9а, то эффект от такого преобразования заключается в получении изображения более высокого контраста по сравнению с оригиналом. Данное преобразование известно как усиление контраста и относится к группе методом поэлементной обработки изображений.
В предельном случае, показанном на рисунке 9б, оператор T(r) обеспечивает двухградационное или бинарное изображение. Отображение такой формы называют пороговой функцией.
Градационные преобразования классифицируются на следующие группы методов: линейные (негатив и тождественное преобразование), логарифмические и степенные.

Рисунок 10 – Основные функции градационных преобразований
Преобразование изображения в негатив
Преобразования изображения в негатив с яркостями в диапазоне [0, L–1] осуществляется с использование негативного преобразования, определяемого выражением:
S= L –1– r
Данный тип обработки подходит для усиления белых или серых деталей на фоне темных областей изображения, особенно когда темные области имеют преобладающие размеры.
Логарифмические преобразования
Общий вид логарифмического преобразования выражается формулой:
S= c· log( 1 + r)
Данный вид преобразований отображает узкий диапазон малых значений яркостей на исходном изображении в более широкий диапазон выходных значений. Для больших значений входного сигнала верно обратное утверждение.
Степенные преобразования
Степенные преобразования имеют вид:
S= c∙ rγ
где c и γ – положительные константы.
Заметим, что амплитудная характеристика многих устройств, используемых для ввода, печати или визуализации изображений, соответствует степенному закону. Процедура, используемая для коррекции такой степенной характеристики называется гамма-коррекцией. Например, устройства с ЭЛТ имеют степенную зависимость яркости от напряжения с показателем степени в диапазоне от 1,8 до 2,5. При γ=2,5 подобная система изображения будет иметь тенденцию к воспроизведению изображений темнее, чем они есть на самом деле. Компенсация данного недостатка производится с помощью методов гамма-коррекции: для этого осуществляется предобработка визуализируемого изображения с помощью преобразования вида s=r1/2.5=r0.4
Правильное воспроизведение цветов также требует применения методов гамма-коррекции. Также степенные преобразования могут применяться для улучшения контрастов: уменьшения или увеличения яркости изображений. При γ>1 яркость изображения уменьшается, степенные преобразования в этом случае применяются для устранения слишком светлых участков изображения, при γ<1 яркость изображения увеличивается.
На рисунке 11 показаны исходный снимок, полученный с помощью ЯМР томографа, а также 3 изображения, полученные в результате степенного преобразования исходного изображения при различных значениях коэффициента γ.

Рисунок 11 – Снимок позвоночника человека с переломом; А – исходное изображение получено с помощью ЯМР-томографа, Б – результат степенного преобразования c=1, γ=0,6; В – c=1, γ=0,4; Г – c=1, γ=0,3
Кусочно-линейные преобразования
Кусочно-линейные преобразования применяются для усиления контраста исходного изображения, при этом данный метод обладает большей гибкостью в использовании по сравнению с ранее рассмотренными. На рисунке 12 приведено кусочно-линейное преобразование для усиления контраста.
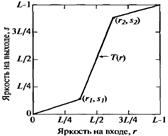
Рисунок 12 – Вид кусочно-линейного преобразования для усиления контраста
Значения (r1, s1) (r2, s2) обеспечивают различные степени растяжения уровней яркости на результирующем изображении, меняя тем самым его контраст. В том случае, если r1=r2, а s1=0 и s2=L–1, то преобразование приводит к получению бинарного изображения. Зачастую наиболее эффективным выбором параметров является следующий: r1=rmin, r2=rmax, s1=0 и s2=L–1, где rmin и rmax означают минимальную и максимальную яркости исходного изображения. Таким образом, функция преобразования линейно растягивает исходный диапазон яркостей в полный диапазон [0, L–1]. Заметим, что соблюдение следующих условий: r1<r2 и s1<s2 означает, что функция преобразования является однозначной и монотонно возрастающей, что в свою очередь, обеспечивает сохранение правильной последовательности уровней яркости, предотвращая тем самым появление ложных деталей на обработанном изображении.
Кусочно-линейные преобразования используются также для вырезания диапазона яркостей на изображении. В практическом применении может потребоваться улучшение контраста отдельных частей изображения, для реализации используются следующие подходы: первый подход состоит в отображении всех тех уровней, которые представляют интерес некоторой одной большой яркостью, а всех остальных уровней – другой низкой яркостью. Такое преобразования в результате дает бинарное изображение. Второй подход заключается в повышении яркостей точек из выбранного диапазона с сохранением яркости фона и остальных участков изображения. На рисунках 13а и 13б приведены функции преобразования, реализующие первый и второй подходы, соответственно.
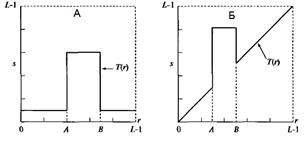
Рисунок 13 – Функции преобразования, реализующие вырезание диапазона
яркостей
Вырезание битовых плоскостей
Вместо выделения диапазонов яркостей, может оказаться полезным выделение информации о вкладе тех или иных битов в общее изображение. Пусть каждый пиксель изображения представлен 8 битами. В этом случае все изображение можно представить себе в виде 8 битовых плоскостей, ранжированных от плоскости 0 с наименее значащими битами до плоскости 7 с наиболее значащими битами.
Старшие биты с 7 по 4 содержат основную часть визуально значимых данных, октальные битовые плоскости с 0 по 3 дают вклад в более тонкие детали изображения. Разделение цифрового изображения на битовые плоскости полезно для анализа относительной информативности, которую несет каждый бит изображения, что позволяет оценить необходимое число битов, требуемое для квантования каждого пикселя. Такая декомпозиция особенно полезна при рассмотрении методов сжатия изображений.
3.2 Видоизменения гистограмм изображения
Гистограммой цифрового изображения с уровнями яркости в диапазоне [0, L–1] называется дискретная функция h(rk)=nk, где rk есть k-й уровень яркости, а nk – число пикселей на изображении, имеющих яркость rk. Обычно гистограмма нормализуется путем деления каждого из ее значений на общее число пикселей в изображении, обозначаемое n. Таким образом, значения нормализованной гистограммы будут определяться как: p(rk)=nk/n, для k=0, 1…, L–1, при этом p(rk) представляет собой вероятность появления пикселя со значением яркости rk, сумма всех значений нормализованной гистограммы равны единице.

Рисунок 14 – Типичные гистограммы для 4-х основных типов изображения
Эквализация гистограммы
Эквализация или линеаризация гистограммы цифрового изображения называется такое преобразование исходного изображения, при котором гистограмма эквализованного изображения перекрывает более широкий диапазон уровней яркости, чем гистограмма исходного изображения. Функция преобразования задается уравнением вида:

Таким образом, суть метода эквализации гистограммы заключается в нахождении функции преобразования, которая стремится сформировать выходное изображение с равномерной гистограммой. Эквализация гистограммы изображения приводит к существенному усилению контраста, к достоинствам метода относится простота его реализации и предсказуемость получаемых результатов.
Тем не мене, в некоторых случаях, улучшение изображения, основанное на модели равномерной гистограммы, не является наилучшим подходом. В некоторых случаях необходимо задавать желаемую форму гистограммы для обрабатываемого изображения. Метод, позволяющий получить обработанное изображение с заданной формой гистограммы, называется методом приведения или задания гистограммы. Данный метод представляет собой итеративную процедуры, заключающуюся в подборе оптимальной формы гистограммы.
Локальное улучшение
Рассмотренный метод гистограммной обработки является глобальным методом, в силу того, что функция преобразования строилась на основе анализа яркостного содержания всего изображения. Существуют случаи, когда приходится улучшать детали изображения посредством анализа малых областей изображения, это связано с тем, что число пикселей в таких областях мало и не оказывает заметного влияния на глобальную гистограмму. Решение заключается в разработке функции преобразования, основанной на распределении яркостей по окрестности каждого элемента изображения.
Процедура состоит в том, что задается форма квадратной или прямоугольной окрестности вокруг обрабатываемого элемента и затем центр этой области перемещается от точки к точке. Для каждого нового положения окрестности определяется гистограмма по входящим в нее точкам и находится функция преобразования эквализации гистограммы. Затем эта функция используется для отображения уровня яркости центрального элемента окрестности, далее центр окрестности перемещается на соседний пиксель и процедура повторяется.
Использование гистограммных статистик для улучшения изображения
Для улучшения изображения можно использовать статистические параметры, получаемые из гистограммы, такие как математическое ожидание и дисперсия.

Математическое ожидание представляет собой меру среднего уровня яркости на изображении, а дисперсия – меру среднего контраста.
В задачах улучшения изображения используются как глобальные статистики, так и локальные. В зависимости от требуемого эффекта обработки изображения суть метода, основанного на использовании гистограммных статистик, заключается в изменении значений яркостей тех пикселей, яркость которых больше или меньше значений локальной или глобальной статистики. Метод позволяет различать светлые или темные участки на изображении, а затем проводить необходимую обработку требуемых локальных областей. Для реализации метода исследователю необходимо задать верхнюю и нижнюю границы контраста, а также определить требуемую область значений яркости.
Пусть f(x, y) исходное значение пикселя в точке (x, y) и g(x, y) – значение того же пикселя, полученного в результате обработки, тогда справедливо выражение:

где: E, k0, k1, k2 – задаваемые параметры метода, MG – глобальное среднее, DG – глобальное стандартное отклонение, mSxy – локальное среднее в окрестности точки с координатами (x, y).
Подбор оптимальных значений параметров требует проведения определенного количества экспериментов и зависит как от вида и структуры самого изображения, так и от субъективного подхода исследователя.
3.3 Методы улучшения изображений на основе арифметико-логических операций
Все арифметико-логические операции над изображениями выполняются поэлементно. Наиболее часто используются операции сложения и вычитания.
В системах медицинской диагностики наибольшее применение вычитание изображений находит при обработке рентгенографических изображений с использованием масок. В частности одним из таких направлений является область медицинской интроскопии на основе рентгенографических методов.
g(x, y)=f(x, y)–h(x, y)
Изображение h(x, y) принято называть маской, в данном случае маска представляет собой рентгеновское изображение интересующего участка тела пациента. Затем вводится рентгеноконтрастное вещество и регистрируется новое изображение – f(x, y). Результирующий эффект вычитания заключается в том, что детали, различающиеся на изображениях f(x, y) и h(x, y), на выходном изображении приобретают повышенный контраст. Рисунок 15 иллюстрирует улучшение изображения путем осуществления операции вычитания.

Рисунок 15 – Улучшение изображения путем вычитания, рисунок слева – изображение-маска, рисунок справа – разность изображения, полученного после введения контрастного вещества в систему кровообращения, и маски
Зачастую изображение может регистрироваться телекамерой, поэтому данное процедура позволяет получить фильм, показывающий, как контрастное вещество распространяется по различным артериям в наблюдаемой области, что позволяет увеличить диагностическую ценность данного исследования.
На практике изображения представляются в виде 8-битового сигнала, тем самым значения изображений не могут выходить за диапазон [0, 255]. На разностном изображении значения могут меняться в диапазоне от –255 до 255, а значит, для воспроизведения результатов необходимо осуществить процедуры масштабирования результирующего изображения. Существует 2 основных варианта такого масштабирования. Первый вариант состоит в прибавлении ко всем значениям константы 255 и последующем делении на 2. Данный метод является быстрым и простым в реализации, однако, его недостатки заключаются в том, что может оказаться задействованным не весь диапазон значений, а также в усечении разностных значений при делении на 2, что означает некоторую потерю в точности. Второй метод заключается в том, что находится минимум разности и полученное значение вычитается из значений всех элементов разностного изображения, тем самым на модифицированном изображении минимальное значение будет рано нулю. Затем все элементы полученного изображения приводятся в интервал [0, 255] умножением на значение 255/Max, где Max – максимальное значение элементов модифицированного изображения. Однако, данный подход более сложен и трудоемок в реализации.
Усреднение изображений
Усреднение изображений зачастую используется для эффективного снижения шумов, присутствующих на изображении. Рассмотрим зашумленное изображение g(x, y), формируемое прибавлением шума η(x, y) к исходному изображению f(x, y):
g(x, y)=f(x, y)+η(x, y)
Предполагается, что значения шума в каждой точке (x, y) является некоррелированными и имеют нулевое среднее значение. Целью усреднения серий изображений, отличающихся только шумом, является уменьшение уровня зашумленности и повышения качества изображения. Пусть изображение  получено усреднением K изображений g i (x, y):
получено усреднением K изображений g i (x, y):

Математическое ожидание и дисперсия  определяется как:
определяется как:

Стандартное отклонение в каждой точке усредненного изображения будет определяться как:

Таким образом, очевидно, что при увеличении числа суммируемых изображений, уровень шума уменьшается. На практике последовательность суммируемых изображений может быть получена в процессе накопления, при этом все изображения должны быть совмещенными, чтобы уменьшить влияние расфокусировки или других искажении на выходном изображении.
3.4 Основы пространственной фильтрации
Локальные преобразования оперируют одновременно как со значениями пикселей в окрестности, так и с соответствующими им значениями некоторой матрицы, имеющей те же размеры, что и окрестность, такую матрицу принято называть фильтром, маской, ядром, шаблоном или окном. Схема пространственной фильтрации проиллюстрирована на рисунке 16, процесс основан на простом перемещении маски фильтра от точки к точке изображения, в каждой точке (x, y) отклик фильтра вычисляется с использованием предварительно заданных связей.

Рисунок 16 – Схема пространственной фильтрации
Фильтрация изображения f, имеющего размеры M×N с помощью фильтра размерами m×n задается выражением общего вида:

где: a=(m–1)/2, b=(n–1)/2, x=0, 1, 2…M–1; y=0, 1, 2…N–1.
Для маски размером 3×3 элемента результат линейной фильтрации изображения в точке (x, y) представлено выражением:
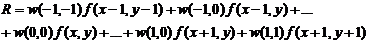
Таким образом, процедура линейной фильтрации представляет собой процедуру свертки коэффициентов фильтра (маски) с отсчетами исходного изображения. В случае, когда интерес представляет только значение отклика R по маске m×n в точке (x, y) используется следующее выражение:

где: wi – коэффициент маски, zi – значение пикселя, соответствующего данному коэффициенту, m· n – общее число коэффициентов в маске.
Сглаживающие пространственные фильтры
Сглаживающие фильтры применяются для расфокусировки изображения и подавления шума. Расфокусировка применяется как предварительный шаг обработки изображения, например, для удаления мелких деталей перед обнаружением больших объектов, для устранения разрывов в линиях или деталях.
Линейные сглаживающие фильтры
Отклик или выходной сигнал линейного сглаживающего фильтра представляет собой среднее значение элементов по окрестности, покрытой маской фильтра, что обеспечивает сглаживающий эффект. Такие фильтры иногда также называют низкочастотными фильтрами.
Заменой исходных значений элементов изображения на средние значения по маске фильтра достигается уменьшение резких переходов уровней яркости. Поскольку случайный шум как раз характеризуется резкими скачками яркости, наиболее очевидным применением сглаживания является подавление шума. Однако, негативной стороной применения сглаживающих фильтров является расфокусировка контуров изображения, которые также характеризуются резкими перепадами яркостей. Главное использование сглаживающих фильтров состоит в подавлении несущественных деталей на изображении, под которыми понимается совокупность пикселей, которые малы по сравнению с размерами маски фильтра.

Рисунок 17 – Маски сглаживающих фильтров
Постоянный множитель перед маской равен единице, деленной на сумму значений коэффициентов, множитель необходим для нормировки. Первый фильтр имеет одинаковые коэффициенты и называется однородным усредняющим фильтром, выходное значение данного фильтра представляет собой обычное среднее значение по маске. Вторая маска обеспечивает на выходе фильтра взвешенное среднее, коэффициент в центре маски имеет самое большое значение, значения остальных коэффициентов уменьшаются по мере удаления от центра маски. Основная стратегия применения подобного рода фильтров – уменьшение расфокусировки при сглаживании.
Общая формула фильтрации изображения размерами M×N с помощью фильтра взвешенного среднего по окрестности m×n определяется выражением:

Подбор оптимального размера маски требует проведения нескольких экспериментов и определяется как размерами исходного изображения, так и основным назначением выполнения процедуры сглаживания изображения.
Фильтры, основанные на порядковых статистиках
Фильтры, основанные на порядковых статистиках, относятся к классу нелинейных пространственных фильтров. Отклик такого фильтра определяется предварительным ранжированием значений пикселей, покрываемых маской фильтра. И последующим выбором значения, находящегося на определенной позиции упорядоченной последовательности. Иными словами, фильтрация сводится к замещению исходного значения пикселя (находящегося в центре маски) на полученное значение отклика фильтра.
Наиболее известным является медианный фильтр, который заменяет значение пикселя на значение медианы распределения яркостей всех пикселей в окрестности (включая исходный). Для определенных типов случайных шумов медианные фильтры обеспечивают хорошее подавление шумов при значительно меньшем эффекте расфокусировки, чем у линейных сглаживающих фильтров с аналогичными размерами. Медианные фильтры особенно эффективны при фильтрации импульсных шумов, которые выглядят как наложение на изображение случайных черных и белых точек, такой тип шума называется шумами “соль и перца”.
Медиана набора чисел есть такое число ξ, что половина чисел из набора меньше или равны ξ, а другая половина – больше или равны ξ. Для реализации процедуры медианной фильтрации для элемента изображения необходимо упорядочить по возрастанию пиксели внутри окрестности, затем найти значение медианы и присвоить полученное значение обрабатываемому элементу.
Основная функция медианного фильтра заключается в замене отличающегося от фона значения пикселя на другое значение, более близкое к его соседям. Изолированные темные или светлые (по сравнению с окружающим фоном) кластеры, имеющие площадь не более n2/2 (половина площади маски фильтра), будут удалены медианным фильтром с маской размерами n×n, при этом кластеры больших размеров искажаются значительно меньше.
Помимо медианного фильтра к фильтрам, основанным на порядковых статистиках, также относят фильтр максимума и фильтр минимума. В фильтре максимума в качестве порогового отсчета используется 100-й перцентиль, в фильтре минимума – 0-й перцентиль. Данные типы фильтров полезны при нахождении наиболее ярких или наиболее темных точек по отношению к окружающему фону.
3.5 Пространственные фильтры повышения резкости изображений
Главная цель повышения резкости заключается в том, чтобы подчеркнуть мелкие детали изображения или улучшить те детали, которые оказались расфокусированы вследствие ошибок или несовершенства самого метода регистрации изображений.
Ранее было показано, что расфокусировка изображения осуществлялась путем усреднения значений пикселей по окрестности. Повышение резкости изображения может быть достигнуто с помощью обратной процедуры – пространственного дифференцирования.
Дифференцирование изображения позволяет усилить перепады и другие разрывы на изображении, но также неизбежно приводит и к усилению шумов на изображении. Величина отклика оператора производной в точке изображения пропорциональна степени разрывности изображения в данной точке.
Производные дискретной функции определяются в терминах разности. Первая производная должна быть:
1) равной нулю на участках с постоянным уровнем яркости;
2) ненулевой в начале и в конце ступеньки или склона яркости;
3) ненулевой на склонах яркости.
Вторая производная должна быть:
1) равной нулю на участках с постоянным уровнем яркости;
2) ненулевой в начале и в конце ступеньки или склона яркости;
3) равной нулю на склонах постоянной крутизны.
Первая производная одномерной функции определяется как разность значений соседних элементов:

Аналогично вторая производная определяется как разность соседних значений первой производной:
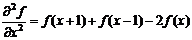
Отметим, что вторая производная является намного более эффективной при решении задач усиления резких переходов на изображении чем первая производная, однако, вторая производная обеспечивает намного большее усиление мелких деталей, включая шум.
Улучшение изображений с использованием вторых производных: лапласиан
В данном случае рассматривается использование оператора двумерной второй производной в задачах улучшения изображения. Подход сводится к выбору дискретной формулировки второй производной и к последующему построению маски фильтра, основанной на предложенной формулировке. В данных задачах рассматриваются исключительно изотропные фильтры, отклик которых не зависит от направления неоднородностей на обрабатываемом изображении. Изотропные фильтры обладают свойством инвариантности к повороту изображения, то есть поворот изображения и последующее применение фильтра дает тот же результат, что и первоначальное применение фильтра с последующим поворотом результата.
Простейшим оператором, основанным на производных, является оператор Лапласа – лапласиан, который для функции двух переменных определяется как:

Для применения оператора Лапласа в цифровой обработке изображений его необходимо выразить в дискретном виде. Наиболее часто используется следующее представление:


Дискретная формулировка двумерного лапласиана получается объединением этих двух составляющих:

Данное уравнение может быть реализовано с помощью маски, представленной на рисунке 18.

Рисунок 18 – Маска фильтра, используемая для реализации дискретного лапласиана
Данная маска дает изотропный результат для поворотов на углы, кратные 900. В формулу дискретного лапласиана могут быть включены диагональные направления добавлением еще двух членов – по одному для каждого из диагональных направлений. Маска, соответствующая такому определению, представлена на рисунке 19. Данная маска является изотропной для поворотов на углы, кратные 450.
В силу того, что оператор Лапласа по сути является второй производной, его применение подчеркивает разрывы уровней яркостей на изображении и подавляет области со слабыми изменениями яркостей. Это приводит к получению изображения, содержащего сероватые линии на месте контуров и других разрывов, наложенные на темный фон без особенностей. Для восстановления прежнего фона при сохранении эффекта повышения резкости, достигаемого использованием лапласиана, достаточно сложить исходное изображение и изображение, получаемое на выходе оператора Лапласа.
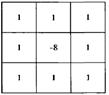
Рисунок 19 – Маска фильтра, используемая для реализации дискретного
лапласиана, полученная с учетом диагональных направлений
Необходимо отметить, что результаты, получаемые с применением маски, содержащей диагональные элементы (рисунок 19), являются более резкими, чем с применением первичной маски, приведенной на рисунке 18.
Нерезкое маскирование и фильтрация с подъемом высоких частот
Процедура, использующаяся для повышения резкости изображения, заключающаяся в вычитании из исходного изображения его расфокусированной копии называется нерезким маскированием и выражается следующей формулой:

где: fs(x, y) – изображение с повышенной резкостью, полученное методом нерезкого маскирования,  – расфокусированная копия исходного изображения f(x, y).
– расфокусированная копия исходного изображения f(x, y).
Обобщенной операцией нерезкого маскирования является фильтрация с подъемом высоких частот, которая задается в следующем виде:

где А ≥1.
При увеличении А больше 1, эффект увеличения резкости становится меньше. Типичным применением фильтрации изображений с подъемом высоких частот является случай, когда исходное изображение темнее, чем это требуется. Варьированием постоянного коэффициента А удается добиться общего увеличения яркости изображения и получить желаемый результат.
Улучшение изображений с использованием первых производных: градиент
В обработке изображений первые производные реализуются через модуль градиента. Для функции f(x, y) градиент f в точке (x, y) определяется как двумерный вектор-столбец:

Модуль этого вектора часто называют градиентом, который определяется следующим образом:

В силу большего объема вычислений, необходимых для обработки всего изображения оператором градиента, на практике часто используют приближенное значение в виде:

Определим дискретные приближения приведенных уравнений. Для указания пикселей в окрестности 3×3 будем использовать обозначения, представленные на рисунке 20.

Рисунок 20 – Область изображения размером 3×3 элемента
Простейшими приближениями первой производной являются следующие выражения: Gx=z8–z5 и Gy=z6–z5. Робертс предложил использовать перекрестные направления: Gx=z9–z5 и Gy=z8–z6. В этом случае градиент будет определяться следующим выражением:

В случае использования приближенной формулы для определения градиента:

Приведенное уравнение может быть реализовано с помощью масок, приведенных на рисунке 21.

Рисунок 21 – Маски 2×2, используемые для вычисления градиента
Данные маски называют перекрестным градиентным оператором Робертса. Однако, маски четного размера неудобны в своей реализации, поэтому более предпочтительным является применение масок с минимальным размером окрестности 3×3, в этом случае градиентный оператор может быть реализован с помощью следующего выражения:

Соответствующие маски приведены на рисунке 22. Представленные маски называют оператором Собела.
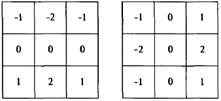
Рисунок 22 – Маски 3×3, используемые для вычисления градиента
Использование весовых коэффициентов со значением 2 основано на стремлении присвоить центральным точкам большую значимость и тем самым достичь большей гладкости. Заметим, что сумма коэффициентов каждой из масок равна 0, что обеспечивает нулевой отклик операторов первой производной на участках изображения с постоянным уровнем яркости, что соответствует требованиям к оператору первой производной. Градиентные операторы применяются для улучшения контуров, в задачах улучшения видимости дефектов и для удаления слабо меняющихся характеристик фона.
3.6 Комбинированные методы пространственного улучшенияизображений
При решении конкретных задач обработки биомедицинских изображений для достижения приемлемого результат может потребоваться применение нескольких дополняющих друг друга пространственных методов улучшения изображения.
В клинической диагностике используются полные снимки скелета, полученные с помощью гамма-лучей для обнаружения таких заболеваний, как костные инфекции и опухоли. Одной из актуальных задач обработки такого рода изображений является повышение резкости изображения для более подробного выявления деталей скелета. Зачастую такие изображения характеризуются малым динамическим диапазоном уровней яркости и высоким содержанием шума, что затрудняет реализацию поставленных задач.
Стратегия обработки данного вида изображений состоит в использовании лапласиана для выделения мелких деталей скелета и градиента для улучшения выступающих краев, а также градационного преобразования для увеличения динамического диапазона яркостей.
На рисунке 23 Б приведен лапласиан, полученный фильтрацией исходного изображения, для лучшего воспроизведения это изображение было подвергнуто градационной коррекцией. Более резкое изображение приведено на рисунке 23 В, полученное сложением исходного изображения А и изображения Б, однако, изображение В содержит высокий уровень шумов. Уменьшить уровень шумов можно с помощью медианной фильтрации, однако, медианная фильтрация является нелинейно операцией, способной удалить мелкие детали изображения, что может оказаться неприемлемым в данной ситуации.
Альтернативным подходом является использование маски, формируемой путем сглаживания градиента исходного изображения. Оператор второй производной (лапласиан) обеспечивает значительное улучшение отображения мелких деталей изображения, по сравнению с градиентом, однако, при этом лапласиан усиливает шум в большей степени, чем градиент. Градиент по сравнению с лапласианом дает более сильный отклик в областях со значительными изменениями яркости (яркостные переходы и ступеньки), при этом отклик градиента на шум и мелкие детали слабее, чем у лапласиана, и может быть в дальнейшем дополнительно снижен путем сглаживания градиента усредняющим фильтром.
На рисунке 23 Г показан градиент, полученный фильтрацией исходного изображения оператором Собела. Контуры на этом изображении выделяются сильнее, чем на изображении-лапласиане (рисунок 23 В).
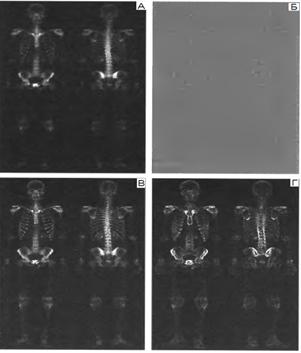
Рисунок 23 – А – полный снимок скелета, Б – применение оператора Лапласа к изображению А, В – повышение резкости сложением изображений А и Б, Г – применение оператора Собела к изображению А
На рисунке 24 А приведено сглаженное градиентное изображение с рисунка 23 Г, полученное с использованием усредняющего фильтра в окрестности 5×5. Результат перемножения лапласиана (рисунок 23 В) и сглаженного градиента (рисунок 24 А) приведен на рисунке 24 Б. Заметное преобладание резких контуров и относительное снижение уровня наблюдаемого шума явилось результатом маскирования лапласиана сглаженным градиентным изображением. На рисунке 24 В приведено изображение с повышенной резкостью, полученное суммированием исходного изображения (рисунок 23 А) и изображения, представленного на рисунке 24 Б. Данное улучшение резкости недостижимо при использовании одного только лапласиана или градиента.
Рассмотренные выше процедуры не влияют на динамический диапазон яркостей изображения, на рисунке 24 Г представлено финальный результат обработки изображения, полученный в результате применения процедуры градационной коррекцией по степенному закону изображения, представленного на рисунке 24 В.

Рисунок 24 – А – изображение на рисунке 19Г, сглаженное усредняющим фильтром по окрестности 5×5, Б – изображение-маска, полученное перемножением изображения на рисунке 19В и изображения А, В – изображение с повышенной резкостью, полученное сложением изображения на рисунке 19А и изображения Б, Г – изображение, полученное градационной коррекцией по степенному закону изображения В






