Все данные материального мира несут в себе информацию о происходящих событиях, являясь по сути регистрацией сигналов, возникающих в результате этих событий. Но данные не тождественны информации. Во многих случаях для того, чтобы получить информацию об объекте, данные надо преобразовать. Это обработка данных. Для обработки данных обязательно применяется какой-нибудь метод.
Представление об информации различается в разных науках. В информатике это первичное понятие. Такие понятия вводятся аксиоматически, т. е. не определяются, а лишь поясняются. В простейшем бытовом понимании с термином "информация" обычно ассоциируются некоторые сведения, данные, знания и т. п.
Информация — это продукт взаимодействия данных и адекватных им методов обработки. Для передачи информации необходима какая-нибудь среда, которая называется каналом связи. Информация имеет некоторый набор свойств. Кроме того, она подразумевает некую возможность ее измерения в количественном или качественном плане.
(слайд) Информация обладает рядом свойств, отличающих ее от других объектов природы.
Дуализм информации характеризует ее двойственность. С одной стороны информация объективна в силу объективности данных, с другой — субъективна, в силу субъективности применяемых методов. Понятие объективности и субъективности информации является относительным. Например, два человека читают одну и ту же книгу и получают подчас весьма разную информацию, хотя прочитанный текст, т. е. данные были одинаковы.
Полнота информации. Это свойство характеризует качество информации, т. е. степень достаточности данных для принятия решения. Неполный набор данных оставляет большую долю неопределенности, в то же время избыточный набор создает повышенный информационный шум и вызывает необходимость применения дополнительных методов, например, фильтрации, сортировки и т. п.
Достоверность информации — это степень соответствия информации реальному объекту с необходимой точностью, т. е. проблема разделения полезного сигнала и шумов. При увеличении уровня шумов достоверность информации снижается.
Адекватность информации есть степень соответствия реальному объективному состоянию дела. Неадекватная информация может образовываться при создании новой информации на основе неполных или недостоверных данных. Получение адекватной информации также затрудняется при недоступности адекватных методов.
Доступность информации - это возможность получения информации при необходимости. Доступность складывается из двух составляющих: из доступности данных и доступности методов.
Актуальность информации - это степень соответствия информации текущему моменту времени. Информация может устаревать. Поскольку информационные процессы растянуты во времени, то достоверная и адекватная, но устаревшая информация может приводить к ошибочным решениям.
Информация в виде сообщения передается с помощью носителя информации в виде сигналов.
Сигнал - это изменяющийся во времени физический процесс. Он может быть дискретным или непрерывным (рис. 1 а, б). Пример дискретного сообщения — процесс чтения книги, информация в которой представлена дискретной последовательностью букв. Пример непрерывного сообщения — человеческая речь, передаваемая модулированной звуковой волной. Непрерывное сообщение можно преобразовать в дискретное (такая процедура называется дискретизацией). Возможность дискредитации непрерывного сигнала с любой желаемой точностью принципиально важна с точки зрения информатики. Компьютер — цифровая машина, т. е. внутреннее представление информации в нем дискретно. Теоретическая база возможности дискретизации непрерывного сигнала заложена следующей теоремой.
Теорема 1.1 (теорема Котельникова[1]). Если непрерывный сигнал имеет спектр, ограниченный сверху частотой 
, то этот сигнал полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал 
.
 |
Из этой теоремы следует, что, во-первых, непрерывная информация может быть дискретизирована, во-вторых, что после дискретизации непрерывный сигнал может быть восстановлен точно.
Рис. 1. Непрерывный и дискретный сигналы
Информация передается в виде сообщений, т. е. данных.
Данные — это зарегистрированные сигналы — объективная часть информации. Метод регистрации данных может быть любым: механическим, физическим, химическим и т. д. В соответствии с методом регистрации данные могут храниться и транспортироваться на носителях разных видов. Распространенными носителями являются бумага, магнитные ленты и диски, оптические диски (CD-ROM), фотографии. Любой носитель характеризуется разрешающей способностью (количество данных, записанных в принятой для носителя единице измерения) и динамическим диапазоном (логарифмическим отношением интенсивности амплитуд максимального и минимального регистрируемого сигнала).
(слайд) Различают следующие основные операции с данными:
сбор данных — это накопление информации;
формализация данных — приведение данных, поступающих из разных источников, к одинаковой форме;
фильтрация данных — уменьшение уровня шума, повышение уровня достоверности и адекватности;
сортировка данных — упорядочение по заданному признаку с целью удобства;
архивация данных — организация хранения в удобной и легкодоступной форме;
защита данных — комплекс мер, направленных на предотвращение утраты, воспроизведения и модификации данных;
транспортировка данных — прием и передача данных между участниками информационного процесса;
преобразование данных — перевод их из одной формы в другую в связи с изменением, например, вида носителя.
Цифровой компьютер — это машина, которая может решать задачи, выполняя данные ей команды. Последовательность команд, описывающих решение определенной задачи, называется программой. Электронные схемы каждого компьютера могут распознавать и выполнять ограниченный набор простых команд. Все программы перед выполнением должны быть превращены в последовательность таких команд, которые обычно не сложнее чем:
• сложить 2 числа;
• проверить, не является ли число нулем;
• скопировать кусок данных из одной части памяти компьютера в другую.
Эти примитивные команды в совокупности составляют язык, на котором люди могут общаться с компьютером. Такой язык называется машинным языком. Разработчик при создании нового компьютера должен решать, какие команды включить в машинный язык этого компьютера. Это зависит от назначения компьютера, от того, какие задачи он должен выполнять. Обычно стараются сделать машинные команды как можно проще, чтобы избежать сложностей при конструировании компьютера и снизить затраты на необходимую электронику. Так как большинство машинных языков очень примитивны, использовать их трудно и утомительно.
Это простое стремление порождает сложности при общении с компьютером. Что понятно и просто пользователю совершено не приемлемо для компьютера. Это привело к построению ряда уровней на каждом из которых происходит преобразование программ и данных к виду более понятному для машины и в конечном итоге к последовательности элементарных (примитивных) команд. Такой подход носит название многоуровневой компьютерной организацией.
Итак, существует огромная разница между тем, что удобно для людей, и тем, что удобно для компьютеров. Люди хотят сделать X, но компьютеры могут сделать только Y. Из-за этого возникают проблемы.
История развития компьютеров показала, что это противоречие решается двумя способами. Оба эти способа включают в себя разработку новых команд, которые более удобны для человека, чем встроенные машинные команды.
В первом случае, выполнение программы, написанной на языке понятном человеку, производится путем замены каждой команды на эквивалентный набор команд в языке понятном машине. В этом случае компьютер выполняет новую программу, написанную на машинном языке, вместо программы, написанной на понятном человеку. Эта технология называется трансляцией, преобразующая программа называется транслятором.
Второй способ — каждая команда из программы написанной на языке понятном человеку преобразуется в набор команд машинного языка и выполняется по очереди.
Эта технология не требует составления машинной программы. Она называется интерпретацией, а программа, которая осуществляет интерпретацию, называется интерпретатором.
Следует заметить, что команды программы написанные на языке понятном человеку называются операторами (каждые представляет набор машинных команд).
Трансляция и интерпретация сходны. При применении обоих методов компьютер в конечном итоге выполняет набор команд на машинном языке, эквивалентных командам исходной программы. Различие лишь в том, что при трансляции вся исходная программа переделывается в машинную, загружается в память компьютера и затем выполняется.
При интерпретации каждая команда (оператор) исходной программы перекодируется в машинную и сразу же выполняется.
Такой подход приводит к тому, что выполнение программы производится в несколько этапов (допустим n) на каждом из которых производятся соответствующие преобразования. Таким образом компьютер должен обеспечивать преобразования на n уровнях.
Человеку, который пишет программу n -го уровня, не обязательно знать о трансляторах и интерпретаторах более низких уровней. Машина выполнит эти программы, и не важно, будут ли они выполняться шаг за шагом интерпретатором или их будет выполнять сама машина. В обоих случаях результат один и тот же: программа будет выполнена.
Большинство программистов, пишущих программы n уровня, интересуются только самым верхним уровнем, то есть уровнем, который меньше всего сходен с машинным языком. Однако те, кто хочет понять, как в действительности работает компьютер, должны изучить все уровни. Те, кто проектирует новые компьютеры или новые уровни (то есть новые виртуальные машины), также должны быть знакомы со всеми уровнями.
Большинство современных компьютеров состоит из двух и более уровней. Существуют машины даже с шестью уровнями (слайд). Уровень 0 — аппаратное обеспечение машины. Его электронные схемы выполняют программы, написанные на языке уровня 1. Ради полноты нужно упомянуть о существовании еще одного уровня, расположенного ниже уровня 0. Этот уровень не показан, так как он попадает в сферу электронной техники и, следовательно, не рассматривается в этой книге. Он называется уровнем физических устройств. На этом уровне находятся транзисторы, которые являются примитивами для разработчиков компьютеров.
Объяснять, как работают транзисторы, — задача физики Вы будете их изучать в дисциплине Радиоматериалы и компоненты.
На самом нижнем уровне, цифровом логическом уровне, объекты называются вентилями. Хотя вентили состоят из аналоговых компонентов, таких как транзисторы, они могут быть точно смоделированы как цифровые средства. У каждого вентиля есть одно или несколько цифровых входных данных (сигналов, представляющих 0 или 1). Вентиль вычисляет простые функции этих сигналов, такие как И или ИЛИ. Каждый вентиль формируется из нескольких транзисторов. Несколько вентилей формируют 1 бит памяти, который может содержать 0 или 1. Биты памяти, объединенные в группы, например, по 16, 32 или 64, формируют регистры. Каждый регистр может содержать одно двоичное число до определенного предела.
Вентили и булева алгебра
Цифровые схемы могут конструироваться из небольшого числа простых элементов путем сочетания этих элементов в различных комбинациях.
Вентили
Цифровая схема — это схема, в которой есть только два логических значения. Обычно сигнал от 0 до 1 В представляет одно значение (например, 0), а сигнал от 2 до 5 В — другое значение (например, 1). Напряжение за пределами указанных величин недопустимо. Крошечные электронные устройства, которые называются вен тилями, могут вычислять различные функции от этих двузначных сигналов. Эти вентили формируют основу аппаратного обеспечения, на которой строятся все цифровые компьютеры.
Описание принципов работы вентилей не входит в наше изучение, поскольку это относится к уровню физических устройств, который находится ниже уровня 0. Тем не менее, основной принцип, очень простой.
Вся современная цифровая логика основывается на том, что транзистор может работать как очень быстрый бинарный переключатель. На рис. 2, а изображен биполярный транзистор, встроенный в простую схему. Транзистор имеет три соединения с внешним миром; коллектор, базу и эмиттер. Если входное напряжение Vcc ниже определенного критического значения, транзистор выключается и действует как очень большое сопротивление. Это приводит к выходному сигналу V ou t, близкому к Vcc (напряжению, подаваемому извне), обычно +5 В для данного типа транзистора. Если V i n превышает критическое значение, транзистор включается и действует как провод, вызывая заземление сигнала V ou t.
 |
Важно отметить, что если напряжение Vin низкое, то Vout высокое, и наоборот.
Эта схема, таким образом, является инвертором, превращающим логический 0 в логическую 1 и логическую 1 в логический 0. Резистор нужен для ограничения количество тока, проходящего через транзистор, чтобы транзистор не сгорел. На переключение с одного состояния на другое обычно требуется несколько наносекунд.
На рис. 2, 6 два транзистора соединены последовательно. Если и напряжение V1, и напряжение V2 высокое, то оба транзистора будут служить проводниками и снижать Vout. Если одно из входных напряжений низкое, то соответствующий транзистор будет выключаться и напряжение на выходе будет высоким.
Другими словами, Vout будет низким тогда и только тогда, когда и напряжение V1, и напряжение V2 высокое.
На рис. 2, в два транзистора соединены параллельно. Если один из входных сигналов высокий, будет включаться соответствующий транзистор и снижать выходной сигнал Если оба напряжения на входе низкие, то выходное напряжение будет высоким.
Эти три схемы образуют три простейших вентиля Они называются вентилями НЕ, НЕ-И и НЕ-ИЛИ. Вентили НЕ часто называют инверторами. Мы будем использовать оба термина. Если принять, что высокое напряжение (Vcc) — это логическая 1, а низкое напряжение («земля») — логический 0, то можно выражать значение на выходе как функцию от входных значений. Значки, которые используются для изображения этих трех типов вентилей, показаны на рис. 3, а-в. Там же приводится поведение функции для каждой схемы.
На этих рисунках А и В — это входные сигналы, а X — выходной сигнал. Каждая строка таблицы определяет выходной сигнал для различных комбинаций входных сигналов.
Булева алгебра
Чтобы описать схемы, которые строятся путем сочетания различных вентилей, нужен особый тип алгебры, в которой все переменные и функции могут принимать только два значения: 0 и 1. Такая алгебра называется булевой алгеброй. Она названа в честь английского математика Джорджа Буля (1815-1864). На самом деле в данном случае мы говорим об особом типе булевой алгебры, а именно об алгебре релейных схем, но термин «булева алгебра» очень часто используется в значении «алгебра релейных схем», поэтому мы не будем их различать.
Как и в обычной алгебре (то есть в той, которую изучают в школе), в булевой алгебре есть свои функции. Булева функция имеет одну или несколько переменных и выдает результат, который зависит только от значений этих переменных.
Можно определить простую функцию f, сказав, что f(а)=l, если а=0, и f(а)=0, если а=1. Такая функция будет функцией НЕ (см. рис. 3, а).
Так как булева функция от п переменных имеет только 2" возможных комбинаций значений переменных, то такую функцию можно полностью описать в таблице с 2" строками. В каждой строке будет даваться значение функции для разных комбинаций значений переменных. Такая таблица называется таблицей истинности. Все таблицы на рис. 3 представляют собой таблицы истинности. Если мы договоримся всегда располагать строки таблицы истинности по порядку номеров, то есть для двух переменных в порядке 00, 01, 10, 11, то функцию можно полностью описать 2" -битным двоичным числом, которое получается, если считывать по вертикали колонку результатов в таблице истинности.
Таким образом, НЕ-И - это 1110, НЕ-ИЛИ - 1000, И - 0001 и ИЛИ - 0111. Очевидно, что существует только 16 булевых функций от двух переменных, которым соответствуют 16 возможных 4-битных цепочек. В обычной алгебре, напротив, есть бесконечное число функций от двух переменных, и ни одну из них нельзя описать, дав таблицу значений этой функции для всех возможных значений переменных, поскольку каждая переменная может принимать бесконечное число значений.
 |
На рис. 3, а показана таблица истинности для булевой функции от трех переменных: M=f(a, b, c) Это функция большинства, которая принимает значение 0, если большинство переменных равно 0, и 1, если большинство переменных равно 1. Хотя любая булева функция может быть определена с помощью таблицы истинности, с возрастанием количества переменных такой тип записи становится громоздким. Поэтому вместо таблиц истинности часто используется другой тип записи. Чтобы увидеть, каким образом осуществляется этот другой тип записи, отметим, что любую булеву функцию можно определить, указав, какие комбинации значений переменных дают значение функции 1. Для функции, приведенной на рис. 4, а, существует 4 комбинации переменных, которые дают значение функции 1. Мы будем рисовать черту над переменной, чтобы показать, что ее значение инвертируется. Отсутствие черты означает, что значение переменной не инвертируется. Кроме того, мы будем использовать знак умножения (точку) для обозначения булевой функции И (знак умножения может опускаться) и + для обозначения булевой функции ИЛИ.
| А | В | Х |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Например, AB принимает значение 1, только если А=1, В=0. В таблице на рис. 4, а функция принимает значение 1 в 2-х строках: AB, AB. Функция Х принимает значение истины (то есть 1), если одно из этих двух условий истинно. Следовательно, мы можем написать
Х=АВ+АВ.
Это компактная запись таблицы истинности.
Системы счисления
Общие сведения
Системой счисления называется принятый способ записи чисел и сопоставления этим записям реальных значений. (слайд) Все системы счисления разделяются на два класса: позиционные и непозиционные.
Позиционной системой счисления называется такое представление чисел, в котором последовательные числовые разряды являются последовательными целыми степенями некоторого целого числа, называемого основанием системы счисления. Основание системы счисления — это отношение соседних разрядов числа. Позиционные системы для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т. е. от позиции, занимаемой цифрой.
Непозиционные системы для записи числа используют бесконечное множество символов, и значение символа не зависит от того места, которое он занимает в числе. Примером непозиционной системы может служить римская система счисления. Например, числа один, два и три кодируются буквой I: I, II, III. Для записи числа пять выбирается новый символ V, для десяти — Х и т. д. Кроме сложной записи самих чисел такая форма их представления приводит к очень сложным правилам арифметики.
Число в позиционной системе счисления с основанием 
может быть представлено в виде многочлена по степеням следующим образом:
,
где 
— запись числа в системе счисления с основанием 
, 
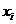— цифра в 
-ом разряде, 
— число разрядов целой части, 
- число разрядов дробной части.
Записывая слева направо числа, получим закодированную запись числа в -ичной системе счисления 
.
В двоичной системе счисления все арифметические действия выполняются весьма просто, например таблица сложения и умножения будет иметь восемь правил (табл. 2). Однако запись числа в двоичной системе счисления длиннее записи того же числа в десятичной системе счисления в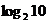 
раз (примерно в 3.3 раза). Это громоздко и неудобно для использования.
Наряду с двоичной системой в информатике применяются восьмеричная и шестнадцатеричная системы счисления. Восьмеричная система счисления имеет восемь цифр (0, 1, 2, 3, 4, 5, 6, 7), шестнадцатеричная — шестнадцать (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Таблица 2. Арифметические действия в двоичной системе счисления
| Сложение | Умножение |
| 0+0=0 | 0×0=0 |
| 0+1=1 | 0×1=0 |
| 1+0=1 | 1×0=0 |
| 1+1=10 | 1×1=1 |
Если из контекста не ясно, к какой системе счисления относится запись, то основание системы записывается после числа в виде нижнего индекса. Например, одно и то же число 137 запишется в двоичной, восьмеричной и шестнадцатеричной системе следующим образом: 
.
Арифметические действия с числами в восьмеричной и шестнадцатеричной системах счисления выполняются по аналогии с двоичной и десятичной системами. Для этого необходимо воспользоваться соответствующими таблицами (например, табл. 3).
Таблица 3. Арифметические действия в восьмеричной системе счисления
| Сложение | Умножение | ||||||||||||||||
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 3 | 0 | 3 | 6 | 11 | 14 | 17 | 22 | 25 |
| 4 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 |
| 5 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 5 | 0 | 5 | 12 | 17 | 24 | 31 | 36 | 43 |
| 6 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 6 | 0 | 6 | 14 | 22 | 30 | 36 | 44 | 52 |
| 7 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 |
