Динамический массив обычно передается в подпрограмму по значению, т.к. сама переменная уже является ссылкой:
procedure Squares(a: array of integer);
begin
for var i:=0 to a.Length-1 do
a[i]:= Sqr(a[i]);
end;
begin
var a:= Arr(1,3,5,7,9);
Squares(a);
end.
Динамический массив передается по ссылке только в одном случае: если он создается или пересоздается внутри подпрограммы. В частности, это необходимо делать если для динамического масива внутри подпрограммы вызывается SetLength:
procedure Add(var a: array of integer; x: integer);
begin
SetLength(a,a.Length+1);
a[a.Length-1]:= x;
end;
begin
var a:= Arr(1,3,5,7,9);
Add(a,666);
writeln(a);
end.
Задача о движении артиллерийского снаряда относится к задачам внешней баллистики. Не останавливаясь на вопросах внутренней баллистики, рассмотрим движение снаряда как тела, принимаемого за материальную точку, брошенного под углом к горизонту с некоторой начальной скоростью 
. При движении в безвоздушном пространстве на снаряд действует только сила тяжести 
, т.е. он движется с постоянным по величине и направлению ускорением земного притяжения (рис. 1).
Не останавливаясь на достаточно простом выводе уравнений движения снаряда по осям х и у, которые можно получить, составив дифференциальные уравнения движения на основании второго закона динамики или из кинематических соображений, не применяя этот закон.
Приведем эти уравнения.
(1-2)
Определение траектории снаряда
Траекторией называется кривая линия, описываемая центром тяжести снаряда в полете. Уравнение (1) и (2) являются параметрическими уравнениями кривой. Для получения уравнения траектории в координатной форме (в явном виде) исключим из этих уравнений время t, для чего выразим его из уравнения (1) и подставим в уравнение (2), получим
(3)
Полученное уравнение является уравнением траектории в явном виде и графически изображается параболой, общее уравнение которой, как известно из математики [3], имеет вид
(4)
где для нашей задачи
Используя уравнения (1) - (3), можно решить ряд задач по определению многих характеристик движения снаряда.
Определение времени, высоты и дальности полета
Положив в уравнении (2) у = 0, получим
,
Отсюда 
- время начала движения снаряда, 
– время полета.
Подставив 
в уравнение (1) после преобразования получим дальность полета
Максимальную высоту подъема Н определим, продифференцировав уравне- ние (2) по времени и полученное выражение приравняв нулю, т.е. в верхней точке траектории функция имеет максимум или проекция скорости на ось у V y = 0.
,
Отсюда время подъема в верхнюю точку
(6)
т.е. равно половине времени 
полета снаряда.
Тогда
Определение угла при котором дальность полета имеет максимум
Продифференцируем выражение (5) по углу и приравняем его к нулю
Отсюда 
При этом значении угла
Высота подъема
Время подъема на эту высоту
Располагая ствол орудия под различными углами α к горизонту, получим семейство параболических траекторий. Для их построения вычислим максимальные высоты Н и максимальные дальности L полета при различных значениях уг- лов α (табл. 1).
| 10 | 20 | 30 | 45 | 60 | 70 | 80 | 90 |
| 
| 
| 
| 
|
|
| 
| 
|
| 
| 
| 
| 
| 
| 
| 
| 
|
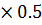
Из таблицы видно, что одинаковые значения дальности полета имеют место при двух разных по величине углах α наклона ствола орудия, из которых, если один 
, то второй 
, т.к. 
.
Построим параболы, отложив по горизонтальной оси значения L, а по вертикальной оси – значения H (рис. 2)
Рисунок 2.
Определение угла 
при котором снаряд попадает в заданную точку с координатами 
.
Преобразуем уравнение (3) траектории движения снаряда с использованием тождества
Получим
После преобразований получим квадратное уравнение относительно 
,
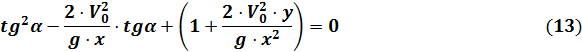
Решение этого уравнения имеет вид
Определение параболы безопасности
Для построения формулы параболы безопасности (огибающая максимальных значений высоты полета снаряда) исследуем на экстремум уравнение (12), для чего возмем производную по и приравняем полученное выражение к нулю.
Отсюда получим
При таком значении функция имеет максимум, после подстановки выражения (15) в (12) получим
После преобразования получим
Это и есть уравнение параболы безопасности
Литература ________________________________________
______________________________________________________
______________________________________________________
Разработал: старший преподаватель С.Приступа
« » ______________ ___ г.
