Преобразование из десятичной в прочие системы счисления производится в соответствии с формулой 1.4.2 с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно. Рассмотрим алгоритм перевода на примере целого числа 137 в двоичную систему. Разделим его нацело на 2, получим 
, остаток 1. Полученный результат можно записать следующим образом: 
. Продолжим операцию деления дальше
, остаток 0, 
;
, остаток 0, 
;
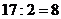, остаток 1, 
;
, остаток 0, 
;
, остаток 0, 
;
, остаток 0, 
.
Далее процесс продолжать нельзя, т. к. 0 не делится нацело на 2. Таким образом, последовательное деление нацело на 2 позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа: 
. Все приведенные выкладки можно сократить, записав процесс деления в виде следующей схемы:
Читая частное и остатки от деления в порядке, обратном получению, найдем двоичную запись числа. Для других систем счисления все описанные действия выполняются аналогичным способом. Например, это же число 137 в восьмеричную и шестнадцатеричную систему счисления переводится по похожим схемам.
Для дробных чисел правило последовательного деления заменяется правилом последовательного умножения. Переведем 0.2 из десятичной системы счисления в двоичную. Умножим 0.2 на 2, т. е. 
или 
.
, 
;
, 
;
, 
;
, 
,
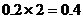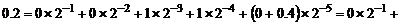
т. е. 
. Все вышеприведенные выкладки можно свести в табл. 4.
Таблица 4
| 0 | 0.2 2 |
| 0 | 0.4 2 |
| 1 | 0.8 2 |
| 1 | 0.6 2 |
| 0 | 0.2 2 |
| … | … |
Заметим, что в десятичной системе правильная дробь переводится в десятичную дробь в конечном виде только тогда, когда ее знаменатель имеет множители только степени двоек и пятерок, т. е. дробь имеет вид 
. Аналогично в двоичной системе счисления конечный вид получают дроби, где в знаменателе только степени двойки. Таким образом, большинство десятичных конечных дробей в двоичной системе счисления будут бесконечными периодическими дробями.
Обратный перевод чисел из двоичной системы счисления в десятичную производится методом подстановки. Для этого необходимо представить число по формуле (1.4.2):
.
Между двоичной системой счисления, восьмеричной и шестнадцатеричной существует связь, позволяющая легко переводить числа из одной системы в другую. Чтобы перевести число из двоичной системы счисления в восьмеричную, надо от десятичной запятой вправо и влево выделить группы по три цифры (триады), и каждую группу независимо от других перевести в одну восьмеричную цифру. Для перевода в шестнадцатеричную систему необходимо выделять по четыре цифры (тетрады) и переводить каждую группу в одну шестнадцатеричную цифру.
