До сих пор мы строили линии нагрузки для постоянного тока. При подаче переменного сигнала на вход усилителя, кроме постоянного тока, через транзистор и элементы схемы протекает ещё и переменный ток. В подавляющем большинстве случаев пути прохождения переменного тока отличаются от путей прохождения постоянного тока. По этой причине нагрузка переменному току отличается от нагрузки постоянному току, а нагрузочная линия переменному току занимает иное положение, чем нагрузочная линия постоянному току.
Когда сигнал переменного напряжения подан на вход схемы, напряжения и токи изменяются по линии нагрузки для переменного тока. Линия нагрузки для переменного тока должна проходить через точку покоя А (UКЭ; IОК), но её наклон определяется величиной сопротивления нагрузки переменному току Rн ~. 
На рис.1.13 показана принципиальная схема каскада транзисторного усилителя с автоматическим смещением или эмиттерной стабилизацией.
| |
Рис.1.13. Принципиальная схема усилительного каскада с ОЭ.
Входнойпеременный сигнал U1 поступает на базу транзистора через разделительный конденсатор Ср1, а выходной сигнал U2 поступает в нагрузку через разделительный конденсатор Ср2, который не пропускает постоянную составляющую в R2н. Конденсатор большой емкости СЭ шунтирует эмиттерный резистор для того, чтобы на эмиттере не появилось переменное напряжение. Без СЭ коэффициент усиления упадет из-за отрицательной ОС, поскольку переменное напряжение на резисторе RЭ вычитается из входного сигнала и на вход транзистора б-э поступает меньшее напряжение UБЭ=UБ – UЭ
Для анализа усилителей на переменном токе используются эквивалентные схемы, в которых все точки, имеющие неизменяемый потенциал по постоянному току, рассматриваются как имеющие нулевой потенциал для переменной составляющей. В области средних частот, на которых и принято строить нагрузочную линию переменному току, влияние конденсаторов на работу схемы можно не учитывать, т.е. можно считать, что все конденсаторы имеют большую ёмкость, являются идеальными и для переменной составляющей представляют короткозамкнутую цепь, а для постоянной составляющей – разомкнутую. Вследствие этого на эквивалентной схеме для переменного тока (рис.1.14а) R1И соединен с базой, R2Н – с коллектором транзистора, а эмиттер соединён с общим проводом (заземлён) благодаря конденсатору СЭ, который имеет большую величину ёмкости, и, следовательно, практически нулевое сопротивление переменному току.
Источники питания постоянного тока обычно обладают большой ёмкостью, которая для переменного сигнала представляет короткозамкнутую цепь. Вследствие нулевого сопротивления источника питания EК переменному току, точка “а” соединяется с общим проводом.
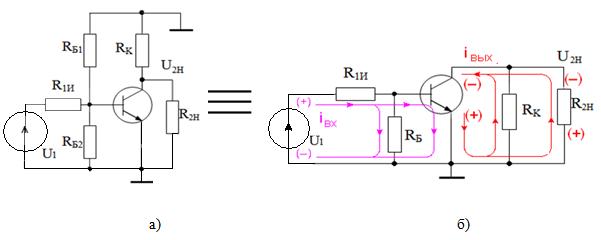
Рис.1.14 Эквивалентная схема для переменного тока на средних частотах усилителя с ОЭ, выполненного по схеме рис.1.13.
На эквивалентной схеме рис.1.14 б показаны пути прохождения входного переменного тока ίвх и пути прохождения выходного переменного тока ίвых. В выходной цепи переменная составляющая коллекторного тока проходит через сопротивление RК и сопротивление внешней нагрузки R2Н. Эти сопротивления включены параллельно и образуют эквивалентное сопротивление нагрузки переменному току RН~=RК·R2Н/(RК+R2Н). Оно и определяет наклон нагрузочной линии переменному току. Поскольку сопротивление нагрузки переменному току Rн~ меньше сопротивления нагрузки постоянному току RН= = RК + RЭ, нагрузочная линия переменному току пройдёт через точку покоя с большей крутизной, чем нагрузочная линия постоянному току.
Уравнение для нагрузочной линии переменному току может быть получено из алгебраического выражения для наклонной линии вида ү – ү 1 = m (х – x 1), где х 1, ү 1 – точки на линии, а m – её наклон. Для схемы на биполярном транзисторе это уравнение удобно представить в виде IОК –iК1= (UКЭ – uк1)/Rн~.
Через приращение тока коллектора ∆ίК=IОК–ίК1 выражаем приращение напряжения ∆uК=UКЭ–uК1 и получаем уравнение нагрузочной линии переменному току ∆ίкRн ~ = – ∆uК.
ПРИМЕР 1.9 Построить нагрузочную линию для переменного тока при сопротивлении внешней нагрузки R2Н = 3кОм
Дано: На рис.1.11 изображена нагрузочная линия
постоянному току при RК=2кОм, RЭ=1,2кОм и указана
точка покоя А с координатамиUКЭ=6 В, IОК=2мА
Решение: Определяем эквивалентное сопротивление
нагрузки выходному переменному току
RН~=RК · R2н/(RК + R2н) =
2кОм · 3кОм/(2 + 3)кОм=1,2кОм.
Линия нагрузки переменному току должна
проходить через точку покоя А и иметь наклон
∆iК/∆uК = –1/R Н~.
Выбирая ∆ίК или ∆uК найдём координаты другой
точки, через которую пройдёт нагрузочная линия
переменному току.
Расчет:
Вариант 1. Задаем приращение тока коллектора.
Пусть ∆iк=1мА, тогда ∆uк = –∆ίк · Rн~ = – 1мА · 1,2кОм= – 1,2В
Координаты точки А' на нагрузочной линии переменному току:
I'К=IОК + ∆ίк=2мА + 1мА=3мА,
U'К=UКЭ +∆uК=6,0 В–1,2В=4,8В.
Вариант 2. Задаем приращение коллекторного напряжения.
Пусть ∆uк=1,2В, тогда ∆ίк= –∆uк/Rн~ = – 1,2В/1,2кОм= – 1мА.
Координаты точки А '':
U''К= UКЭ + ∆uК=6,0В + 1,2 В =7, 2В; І''К = IОК+ ∆ίк=2мА – 1,0мА=1,0мА.
Нагрузочную линию переменному току можно провести через точку покоя А и любую из двух других А' или А''.
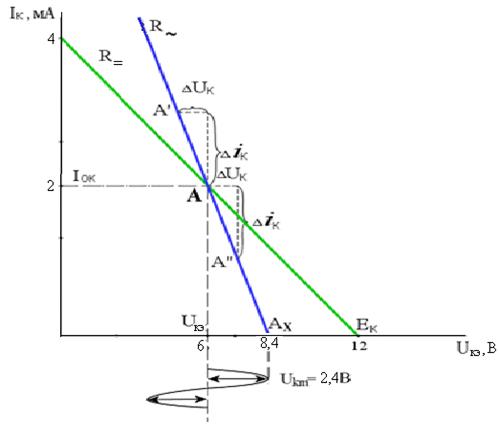
Рис.1.15 Линии нагрузки для постоянного и переменного тока по данным примеров1.5 и, 1.9.
Построение:
Таким образом, если ток ίк увеличится на 1 мА и будет равен 3мА, то uк уменьшится на 1,2В и будет равно 4,8В. Точка А' с координатами
uК =4,8В, ίк=3мА является одной из точек, принадлежащих линии нагрузки для переменного тока. Соединив эту точку с точкой покоя А, получим нагрузочную линию для переменного тока (рис.1.15).
Нагрузочную линию переменному току можно построить также соединив точку покоя А с точкой А'' с координатами ( UК=7,2В; Ік=1мА ).
Заметим, что линия нагрузки переменному току задаёт размах наибольшего переменного напряжения на коллекторе транзистора. Точка Ах имеет координаты:
UК(Х)=UКЭ +∆UК=UКЭ +∆ІОК · RН~ = 6,0В + 2мА · 1,2кОм=8,4В; ІК=0.
Размах сигнала uкm=UКХ – UКЭ=8,4–6,0=2,4В. В данном случае ограничение амплитуды сигнала произойдет в точке Ах. При малой величине напряжения покоя UКЭ на коллекторе транзистора ограничение может возникать слева (при uк=0).При проектировании оконечных каскадов приходится решать задачу выбора точки покоя, чтобы получить ≈максимальное неискажённое напряжение сигнала (слева и справа).
Расчет амплитудно-частотной (АЧХ), фазочастотной (ФЧХ) и переходной (ПХ) характеристик на компьютере.
При использовании программы Fastmean с целью получения АЧХ,ФЧХ и ПХ необходимо выполнить те же этапы, что описаны для расчета по постоянному току.
Первый этап – выбор модели активного элемента – обоснован поведением этого элемента в интересующей нас области частот.
Таким образом, если по постоянному току использовалась модель биполярного транзистора ИТУТ, то и по сигналу следует использовать ту же модель, дополнив ее элементами, описывающими поведение транзистора в области верхних частот.
Такая модель хорошо известна [1--3 ].
Для Fastmean она примет вид (рис.1.16).
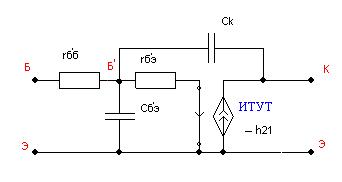
Рис.1.16 Эквивалентная модель биполярного транзистора (ИТУТ) для области верхних частот.
Рассчитаем параметры этой модели:
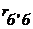- объемное сопротивление базы, = 
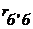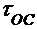/ CК,
где 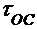- постоянная времени цепи ОС, а CК - емкость коллекторного перехода, приводимые в справочнике.
Сопротивление перехода база-эмиттер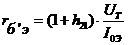 
,
где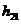 
-коэффициент усиления по току транзистора ОЭ из справочника, а 
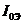-постоянный эмиттерный ток, 
-тепловой потенциал для нормальных условий.
Заметим, что сумма +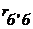 
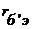= h11.
Емкость 
вычислим, зная частоту единичного усиления транзистора fТ по параметру h21. 
.
ПРИМЕР 1.10 Рассчитать элементы эквивалентной схемы биполярного транзистора по модели рис.1.16.
Дано: Параметры транзистора: h21=150, fТ=200МГц,
CК=12пФ, τОС =100пс, ток покоя Iок=Iоэ=2мА.
Решение: 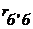= τОС/ CК=100пс/12пФ=8,3пФ,
r б ׳ э =(1+150)*25мВ/2мА=1887 Ом,
=150/(2π*200МГц* 1887Ом)=63,28пФ.
На втором этапе создаем эквивалентную схему по переменному току каскада рис.1.13. Ее вид показан на рис.1.17.
Рис.1.17 Эквивалентная схема по переменному току каскада рис.1.13.
РАСЧЕТ АЧХ И ФЧХ
ПРИМЕР 1.11 Построить АЧХ и ФЧХ усилителя рис.1.13
Дано: Из примера 1.2 RЭ=1.2 кОм, RК=1,8 кОм,
RБ1=62 кОм, RБ2=24 кОм.Сопротивления
источника сигнала R1И=70 Ом, внешней
нагрузки R2Н=400 Ом, ёмкость нагрузки С2Н=10 пФ.
Емкости CР1= CР2=СЭ=1мкФ, элементы
эквивалентной схемы биполярного
транзистора из примера 1.10.
Решение: В эквивалентной схеме рис.1.17 заменяем
транзистор его эквивалентной моделью рис.1.16,
получаем эквивалентную схему усилительного
каскада рис.1.13, удобную для построения частот-
ных характеристик на Fastmean. Эквивалентная
схема по сигналу приведена на рис 1.18
Рис. 1.18 Эквивалентная схема по сигналу усилителя рис.1.13
Параметры усиления тока транзистора h21= -150 А/А. Источник сигнала гармонический. Необходимо помнить, что нумерация элементов зависит от последовательности их набора. Проставив номера узлов, можно приступить к расчету частотных характеристик, воспользовавшись кнопкой ”частотные характеристики” на верхней линейке управления. Масштаб по частоте необходимо установить логарифмический и задать конечную частоту (например f=100 МГц). Масштаб по оси Y выбрать линейный, но в выражение по оси Y ввести db и отношение напряжений в узлах. Так выражение АЧХ по оси Y для примера 1.11 примет вид db(mag(U(5)/U(7)), где U(5) – напряжение на нагрузке R2н (т.е. на выходе каскада), а U(7) – напряжение источника сигнала U1 (рис.1.18). Полученная АЧХ представлена на рис.1.19.
Для определения полосы пропускания по уровню -3дБ необходимо вызвать линейку управления и, установив стрелку на средних частотах, прочитать коэффициент усиления КО дБ. На рис.1.19 КО дБ=20lg(U(5)/U(7))=27,9 дБ.
Частоты среза fн и fв находим по уровню КО дБ-3дБ=24,9 дБ. На рис.1.19
стрелка показывает частоту верхнего среза fв=4,538 МГц. Частота нижнего среза, определяемая таким же способом, fн=12,6 кГц.
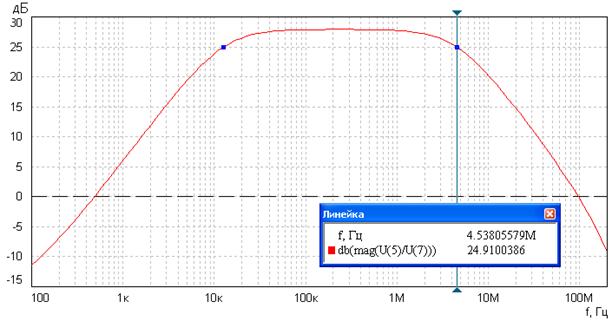
Рис.1.19 АЧХ усилителя рис.1.13 по данным примера 1.11
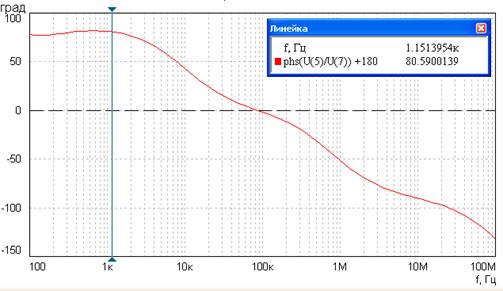
Рис.1.20 АЧХ усилителя рис.1.13 по данным примера 1.11
На рис.1.20 показана ФЧХ этого же усилителя. В учебной литературе принято по ФЧХ определять дополнительный фазовый сдвиг относительно средних частот, при этом фазовый сдвиг на средних частотах принимают за нулевой. В связи с тем, что транзистор, включенный по схеме с ОЭ, дает поворот фазы на – 180о, добавляем 180о в выражение по оси Y. Выражение по оси Y отражается в окне “линейки” (рис.1.20).
