Цепи питания биполярных транзисторов

(схема с эмиттерной стабилизацией)

 

Известно немало схем цепей питания и стабилизации биполярных транзисторов. Одной из распространённых схем цепей питания является схема с эмиттерной стабилизацией ( рис.1.3 ). Эта схема относится к классу схем с автоматическим смещением. Они отличаются от схем с фиксированным смещением тем, что в них при изменении тока коллектора ток базы (или напряжение на базе) автоматически регулируется так, чтобы поддерживать заданный режим.

 

 

Вследствие внешнего сходства расположения резисторов с буквой H (аш), в зарубежной литературе эта структура известна, как схема с H-смещением.

 

 

Рис. 1.3  Схема цепи питания с эмиттерной стабилизацией

 

В исходном (статическом) режиме в схеме текут от плюса источника питания + ЕК к его минусу следующие постоянные токи:

ток покоя коллектора IОК – через резистор RК, через транзистор от коллектора к эмиттеру;

ток покоя базы IОБ – через резистор RБ1, переход база-эмиттер к эмиттеру.

Вытекая из эмиттера эти два тока, образуют эмиттерный  ток IОЭ=IОК+IОБ.  Кроме  этих  токов  в  схеме  протекает   постоянный   ток  через

последовательно соединённые резисторы RБ1 и RБ2. Этот ток принято называть током делителя IД. Так как питание транзистора осуществляется от одного источника питания ЕК, напряжение на базу транзистора подается с делителя напряжения на резисторах RБ1 и RБ2, а именно с резистора RБ2.

Ток эмиттера IОЭ, протекающий через резистор RЭ, создаёт на нём падение напряжения UЭ=IОЭ·RЭ.

Ток делителя создаёт на сопротивлении RБ2 падение напряжения   URБ2=IД·RБ2. Это напряжение соответствует напряжению между базой и общим проводом UБ. В результате напряжение смещения база-эмиттер UОБ=UБ – UЭ=IД·RБ2–IОЭ·RЭ.

 Необходимое напряжение смещения UОБ получают за счёт выбора соответствующих элементов делителя и сопротивления резистора RЭ. Обычно выбором RБ1 и RБ2 устанавливают ток делителя IД>>IОБ. Ток IД=(5…10)IОБ даёт право считать напряжение на базе транзистора фиксированным UБ=IД·RБ2=const.

Динамика процесса стабилизации в рассматриваемой схеме заключается в следующем.

Если под действием какого-либо дестабилизирующего фактора увеличивается ток коллектора IОК↑, то он вызывает рост эмиттерного тока IОЭ↑,

     · · · это приводит к увеличению падения напряжения на резисторе RЭ.

UЭ↑=IОЭ↑·RЭ, 

     · · · увеличение напряжения на эмиттере UЭ↑ до  U'Э =UЭ+∆UЭ при

неизменном напряжении UБ приводит к уменьшению смещения

между базой и эмиттером UОБ ↓ = UБ    U'Э =UБ–UЭ↑.  

     · · · уменьшение смещения на базе UОБ↓ вызывает уменьшение

базового тока IОБ↓,

     · · · уменьшение базового тока IОБ↓ приводит к уменьшению тока

коллектора IОК↓.

 

Краткая запись такого процесса: IОК↓→IОЭ↓→ UЭ↓→UБЭ↑→IОБ↑→IОК↑.

Здесь наблюдаются два воздействия на ток коллектора: прямое, от дестабилизирующих факторов, и обратное - по цепи ОС. Обратите внимание на направления стрелок при IОК. Происходит автоматическая стабилизация тока покоя коллектора IОК.

Высокая стабильность достигается при глубокой ОС. Для этого следует строить звено базового делителя с меньшим номинальным значением сопротивлений RБ1 и RБ2, а в эмиттерной цепи использовать сопротивления RЭ с большими номинальными значениями. К сожалению, сопротивления базового делителя нельзя задавать слишком маленькой величины, так как это приведёт к уменьшению коэффициента усиления, входного сопротивления, и увеличению потребляемой мощности, а RЭ нельзя выбирать слишком большой величины, так как на нём теряется часть напряжения источника питания. Известна рекомендация [4]

RБ=RЭ · h21/10,                                                                                    (1.1)

где RБ  - параллельное соединение RБ1 и RБ2.                          

Для анализа стабилизирующих свойств схемы (рис.1.3) вспомним теорему об эквивалентном генераторе. Заменим принципиальную схему эквивалентной, показанной на рис.1.4. В соответствии с теоремой  Тевенина [6]

ЕБ=ЕК·RБ2/(RБ1 + RБ2),                                                                        (1.2)

RБ=RБ1·RБ2/ (RБ1 + RБ2).      

                                                                            

 

Рис.1.4  Схема с эмиттерной стабилизацией, преобразованная по Тевенину.

   

     Для схемы, приведённой на рис.1.4., можно написать равенство

ЕБ=IОБ·RБ + UБЭ + IОЭ·RЭ.

При нормальной температуре в известном соотношении ίК= ίБ · h21 + IКЭО [7] можно пренебречь обратным током эмиттера IКЭО. Тогда ток покоя коллектора IОК=h21·IОБ.

Выражая ток эмиттера через ток базы IОЭ= IОБ(1+h21), получаем

IОБ=(EБ – UБЭ)/[RБ+(1+h21)·RЭ],                                                         (1.3)                                      

IОК=h21(EБ – UБЭ)/[RБ +(1+h21)RЭ].                                                        (1.4)                                                  

                                            

                    Расчет сопротивлений цепей питания  

 Этот расчёт производится в следующем порядке:

1. Выбираем напряжение источника питания ЕК и сопротивление коллекторной нагрузки RК.  

2. Задаёмся напряжениями на эмиттере и коллекторе.

Напряжение на эмиттере обычно составляет 10–20% от ЕК. Напряжение на коллекторе обычно выбирается равным ЕК/2 или немного больше (например среднее значение между EК и UЭ). Падение напряжения на R Э должно быть больше возможных изменений напряжения U БЭ, но не настолько большим, чтобы заметно уменьшить амплитуду выходного сигнала. Для напряжения на коллекторе имеет место условие U Э < U К< Е К, в то время как при отсутствии R Э U К < Е К.

3. Исходя из заданных значений, определяем RЭ.

4. Выбираем типовое значение h21 транзистора.

5. Используя соотношение (1.2), определяем RБ и ЕБ.

6. Преобразовав выражения для RБ и ЕБ получаем RБ1 =RБ·ЕК/ЕБ,

     RБ2=RБ*R_Б1/(R_Б1–R_Б).

Возможен  другой способ расчета сопротивлений базового делителя. Вместо п.5 и п.6 выбираем ток делителя I_Д=(5…10)* I_{ОБ,  ГДЕ ТОК БАЗЫ}

I_ОБ=I_ОК/h₂₁, напряжение базы U_Б=U_Э+U_{БЭ, СОПРОТИВДЕНИЯ ДЕЛИТЕЛЯ РАВНЫ:}

R_Б1=(E_П-U_Б)/(I_Д+I_ОБ), R_Б2=U_Б/I_Д.

       Номинальные значения сопротивлений резисторов, выпускаемых промышленностью, стандартизованы в соответствии с табл. 1.

      Они выбираются из определенных рядов чисел. Чаще дру­гих используются ряды Е 6, Е 12, Е 24. Цифры после буквы Е указы­вают число номинальных значений в каждом десятичном интервале. При­веденные в рядах числа могут быть продолжены путем умножения или деления этих чисел на 10 в степени n, где n - целое число. Ряды номинальных значений имеют допуск ± 20% (Е 6), ±10% (Е 12), ±5% (Е 24).

 

                                                                                                      Табл.1

E 6	E 12	E 24	E 6	E 12	E 24	E 6	E 12	E 24
1,0   1,5	1,0   1,2   1,5   1,8	1,0 1,1 1,2 1,3 1,5 1,6 1,8 2,0	2,2   3,3	2,2 2,4 2,7   3,3   3,9	2,2 2,4 2,7 3,0 3,3 3,6 3,9 4,3	4,7   6,8	4,7   5,6   6,8   8,2	4,7 5,1 5,6 6,2 6,8 7,5 8,2 9,1

 

  ПРИМЕР 1.1 Рассчитать схему с автоматическим смещением    рис.1.3

                            Дано: ЕК=12В, RК=2кОм, а h21=150

                        Решение: Сначала выбираем значение UК. Допустим что, UК=9В. Тогда падение напряжения на RК равно UR_K = ЕК – UК=12В– 9В=3В.

                                           Теперь проведём расчёт тока покоя коллектора:

                                IОК=UR_К/RК=3В/2кОм=1,5мА.

                                             Ток покоя эмиттера:

                                    IОЭ= IОК ·(1+h21)/h21=1,5мА(101/100)=1,515мА.

                                             Ток покоя базы:

                                        IОБ=IОК/h21=1,5мА/150=10мкА.

Выбрав напряжение эмиттера UЭ=1,7В,       определяем напряжение покоя коллектор–эмиттер UКэ=UК–UЭ==9В–1,7В=7,3В и сопротивление

                                       RЭ=UЭ/IОЭ= 1,7В/1,515мА=1,12кОм.

                                         Согласно рекомендациям (1.2)  

RБ=RЭh21/10=1,12кОм · 150/10=16,8кОм

ЕБ=UЭ + UБЭ + IОБRБ=1,7В + 0,7В + 10мкА · 16,8кОм = 2,568В,

RБ1= RБЕК/ЕБ = 16,8кОм 12В/2,568В = 56кОм,

RБ2 = RБ/ (1–ЕБ/ЕК) = 16,8кОм/ (1–2,568В/12В) = 13,2кОм.

Точка покоя в плоскости входных статических характеристик iБ=f(uБ) определена. Её координаты UБЭ= 0,7В, IОБ =10мкА.

В плоскости выходных статических характеристик iк=f(uк) 

точка покоя имеет координаты UКЭ=7,3В, IОК=1,5мА.

 

ПРИМЕР 1.2  Рассчитать схему с эмиттерной стабилизацией (рис. 1.3) на заданную точку покоя     

                          Дано:(UКЭ=6В, IОК=2мА) при EК=12В, h21=150

                          Решение:Выбираем напряжение эмиттера

                                          UЭ=0,2EК=0,2·12=2,4В, тогда

                                          напряжение UК=UЭ+UКЭ=2,4+6=8,4В,

                                          напряжение UR_К=EК – UК=12–8,4=3,6В.

                                          Сопротивления RК=UR_К/IОК=3,6В/2мА=1,8 кОм,

                                          RЭ=UЭ/IОЭ≈UЭ/IОК≈2,4В/2мА=1,2кОм.

                             Рассчитываем сопротивления базового делителя:

                                          RБ=RЭ·h21/10=1,2кОм·150/10=18кОм,

                                          IОБ=IОК/h21=2мА/150=13мкА,

                                       ЕБ=UЭ+UБЭ+IОБRБ=2,4В+0,7В+13мкА·18кОм=3,34В,

RБ1=RБ·EК/EБ=18кОм·12В/3,34=64,67кОм,

RБ2=RБ*R_Б1/(R_Б1–R_Б)=18кОм*64,67/(64,67–18)=24,97кОм.

 Для реализации схемы рис 1.3 значения сопротивлений выбраны из табл.1:   RЭ=1.2 кОм, RК=1,8 кОм, RБ1=62 кОм, RБ2=24 кОм.

 

 

ПРИМЕР 1.3Рассчитать базовый делитель другим способом

                         Дано: Результаты расчетов примера 1.2.

                         Решение: Выбираем ток делителя I_Д=10*I_{ОБ, ГДЕ   ТОК БАЗЫ} I_ОБ=I_ОК/h₂₁=2/150=0,013 мА, а ток I_Д=10*0,013=0,13 мА.

                                          U_Б = UЭ+UБЭ =2,4+0,7=3,1В        

R_Б2=U_Б/I_Д=3,1/0,13=23,84 кОм,

           R_Б1=(E_К-U_Б)/(I_Д+I_ОБ)=

           (12-3,1)/(0,13+0,013)=60,95 кОм

  Табличные значения резисторов R_Б1 и R_Б2  совпадают с примером 1.2.

 

Проверка расчета сопротивлений цепей питания с помощью компьютера

 

v Для проверки правильности рассчитанных сопротивлений схемы рекомендуем использовать программу “Fastmean”.

Fastmean –это программа анализа схем, основанная на моделировании электрических цепей. С ее помощью можно из введенных в программу элементов “собирать “ на экране исследуемую схему по постоянному токуабилизацией()                                                                         , а также выполнить анализ во временной и частотных областях. Имеется возможность многократного выполнения анализа при изменении параметров элементов схемы (приложение 1).

   Пользование программой можно разбить на 3 этапа:

1.     Выбор модели активных элементов (диода, транзистора,  операционного усилителя);

2.      Создание  эквивалентной схемы и набор модели на экране;

3.      Проведение расчета нужного параметра (ток, напряжение,  АЧХ, ФЧХ,  ПХ).

 

Проведем на компьютере анализ примера 1.2 с целью проверки реализации заданной точки покоя (U_КЭ=6В, I_ОК=2мА) при Е_К=12В, h₂₁=150 и рассчитанных ранее значениях сопротивлений.

Так как схема содержит биполярный транзистор и расчет идет на постоянном токе, то удобнее заменить транзистор источником тока, управляемым током (ИТУТ), как показано на рис.1.5, а.

 

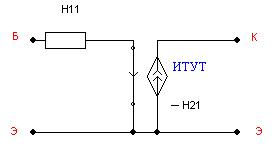
Рис. 1.5,а  Эквивалентная модель биполярного транзистора 

для постоянного тока.

 

    Параметр h_21Э-статический коэффициент передачи тока в схеме с общим эмиттером (ОЭ). В дальнейшем, для удобства h_21Э  заменим на h_21.

Параметр h₂₁ приводится в справочниках на транзисторы. 

Он характеризует усилительные возможности транзистора на переменном токе в области низких частот. Коэффициент усиления на постоянном токе

 H₂₁ ≈ h_21.

 

               H₁₁- входное сопротивление по постоянному току, H₁₁=U_БЭ/I_ОБ.

                      Рис. 1.5,б  показывает различия между входным сопротивлением  биполярного

                транзистора постоянному току H₁₁ и входным сопротивлением переменному

                току  h_11, определяемому касательной к входной характеристике в точке

 покоя А.

 

                   

    Рис. 1.5,б Определение входных сопротивлений биполярного транзистора

               

 

ПРИМЕР 1.4   Вычислить параметры эквивалентной модели биполярного транзистора для постоянного тока.

                        Дано: Транзистор КТ-355А  с коэффициентами

                              усиления тока h₂₁ =  80…300. Ток базы из

                              примера 1.2     I_ОБ=13мкА

                         Решение: Параметры  h₂₁  характеризуют

                                    усиление переменного тока, однако, их

                                    значения практически не отличаются  от

                                    усиления на постоянном токе. Принимаем

                                    среднее значение  h₂₁ = 150.

                                     Напряжение смещения в кремниевых

                                    транзисторах принято считать U_{БЭ =} 0,7В,

                                    откуда  H₁₁=U_БЭ/ I_ОБ =0,7В/13мкА=53,85 кОм

                                                                               

Эквивалентная схема биполярного транзистора представлена на рис. 1.6

Рис.1.6 Эквивалентная схема биполярного транзистора  к Примеру 1.4

 

  Для начала расчета необходимо вызвать программу Fastmean, собрать эквивалентную схему и придать элементам заданные или расчетные значения. После этого проверить соединения во всех узлах и пронумеровать их кнопкой “номера узлов’’, при этом базисный узел не нумеруется.

Вследствие несовпадения направления постоянного коллекторного

тока в реальном транзисторе и в компьютерной модели, коэффициенту передачи тока  h₂₁  необходимо  присвоить  знак  минус (например

h₂₁= – 150А/А).

    Эквивалентная схема каскада примера 1.2, собранная на мониторе, представлена на рис.1.7

 

Рис.1.7 Полученная на мониторе эквивалентная схема каскада примера 1.2 

 

   Расчет постоянных токов и напряжений происходит при нажатии кнопки “переходный процесс “, расположенной на линейке управления вверху экрана. Интересующие токи и напряжения задаются в строчках

“Выражения по оси Y”.

   Ток задается в элементе, через который он протекает, а напряжение - в узлах  или на элементе. Например:

1        t         I(R4)

2        t         U(4)-U(5)

3        t          U(R4)

 

   Результаты расчетов представлены на рис.1.8

t,с

Рис.1.8 Результаты расчетов примера 1.2.

 

Так как единицы измерений токов и напряжений разные и не масштабированы, необходимо нажать кнопку “ показать линейку”,

В результате чего появится окно с расчетными значениями токов и напряжений. Полученный результат подтверждает правильность расчета сопротивлений для реализации точки покоя примера 1.2 (U_КЭ=6В, I_ОК=2мА).   

 

 

Построение нагрузочных линий постоянному току.

На входных статических характеристиках нагрузочная линия строится по уравнению, полученному на основе закона Кирхгофа для базовой цепи (рис.1.4) ЕБ = IБ ·[RБ+ (1 + h21)·RЭ] + UБЭ.

Представленное в виде

,

оно позволяет понять, что эта зависимость соответствует прямой линии вида y=ах+в. Для построения нагрузочной линии рекомендуется использовать два режима [8]: режим холостого хода IБ=0 и режим короткого замыкания UБЭ=0 

При IБ=0  UБЭ=ЕБ, и координаты крайней правой точки Х на нагрузочной линии (рис. 1,а) принимают значения (ЕБ; 0)        

   При UБЭ=0 IБ(Y)=EБ/[RБ+(1+h21)·RЭ], тогда координаты крайней левой  

точки Y на нагрузочной линии (0; IБ(Y)).

 

      ПРИМЕР 1.5   Построить нагрузочную линию на входных статических характеристиках и указать на ней точку покоя

                                         Дано: Результаты расчетов в примерах 1.2 и 1.3

                                      Решение: Координаты крайней правой точки

                                        нагрузочной линии Х (3,34В; 0мкА). В примере 1.2

                                     E_Б=3,34В. Исходя из рис.1.7 уточняем значение

                                     сопротивления R_Б= R_Б1*R_Б2/(R_Б1 + R_Б2)=

                                     62*24/(62+24)=17.3 кОм. При напряжении на

                                      базе UБЭ = 0 получаем ток   IБ(Y)=EБ/[RБ+(1+h21)·RЭ]=

                                     =3,34В/[17.3кОм+(1+150)·1,2кОм]=16,8мкА.

                                     Координаты точки Y (0В; 16,8мкА).

 

IБ мкА

l

Рис.1.9 Нагрузочная линия на входных статических характеристиках.

Рисунок 1.9 иллюстрирует построение нагрузочной линии в плоскости входных статических характеристик. Точка пересечения нагрузочной прямой с входной характеристикой транзистора при заданном UКЭ определяет ток базы и напряжение между базой и эмиттером что соответствует координатам точки покоя А (0,7В; 13мкА), полученным в примерах 1.2 и 1.3

Особенностью входных статических характеристик является то, что ток базы ί Б слабо зависит от напряжения U КЭ. Это приводит к тому что семейство кривых ί Б =ƒ(U Б) при U КЭ≠ 0 на практике сливается и превращается в одну линию [8]. В справочниках обычно приводят две кривые: при U КЭ =0 и при U КЭ≠ 0 (чаще всего это 5B). Естественно, для расчета усилительного каскада используется только одна из них, а именно при U КЭ≠ 0 (рис. 1.1,а).

    ПРИМЕР 1.6Повторить пример1.5 для транзисторов с h21=80 и h21=300.

                            Дано: Результаты расчетов в примерах 1.2 и 1.3

                             Решение:

     1.                h21=80

При UБ=0 IБ(Y) = 3,34В/[17.3кОм+(1+80)1,2кОм]=29мкА

Координаты точки Y (0В; 29мкА), координаты точки Х (3,34 В; 0мкА)

 

Определяем ток покоя базы IОБ=(EБ – UБЭ)/[RБ+RЭ·(1+h21)]=

(3,34–0,7)В/[17.3кОм+(1+80)·1,2кОм]=23мкА.

Это даёт координаты точки покоя А1 (0,7В; 23мкА).

2.                   h21=300

 

Координаты точки Y (0В; 8,8мкА), координаты точки Х (3,34В; 0мкА)

Координаты точки покоя А2 (0,7В; 6,97мкА).

 

На рис.1.10 изображены нагрузочные линии, построенные по данным примеров 1. 6 и 1.5. Штрих - пунктирная линия повторяет нагрузочную линию из рис.1.9

IБ, мкА

UБЭ,В

Рис.1.10 Нагрузочные линии на входных статических характеристиках при различных h21

В плоскости выходных статических характеристик (рис.1.1б) нагрузочная линия строится по уравнению, полученному на базе закона Кирхгофа для выходной цепи, ЕК=IоК·RК+UКЭ+IоЭ·RЭ. Можно показать, что это уравнение также соответствует прямой линии вида y=ах+в. Для определения крайних точек нагрузочной прямой запишем его в виде:

IоК= –UКэ/[RК+RЭ·(1+h21)/h21] + EК/[RК+RЭ·(1+h21)/h21].

Координаты точки X (рис.1.1а)определяются при IК=0, тогда точка Х получает координаты (ЕК; 0). Координаты левой крайней точки Y определяются при UКЭ=0, и они равны (0; IК(Y)), где

IК(Y)= ЕК/[RК + RЭ·(1+h21)/h21].

      ПРИМЕР 1.7   Построить нагрузочную линию в плоскости выходных статических характеристик и указать на ней точку покоя

                          Дано: Результаты расчетов в примерах 1.2 и 1.3

                        Решение:Решение: Координаты точки Х (12В; 0мА).

                          Координаты точки Y

                          (0В, IК(Y)=12В/[1,8кОм+1,2кОм ·151/150] =3,989мА).

                          По данным примера1.2 координаты точки покоя А

                           (UОК=6В; IОК=2мА).

 

Рисунок 1.11  иллюстрирует результаты расчётов по примеру 1.7

Рис.1.11  Нагрузочная линия в плоскости выходных статических характеристик.

 

        ПРИМЕР1.8 Определить координаты точек покоя при h21=80 и h21=300.

                     Дано: Условия примера 1.7

                             Решение:

1.                          h21=80

Координаты точки Х (12В; 0мА), координаты точки Y (0В; 3,989мА), так как (1+h21)/h21≈1.

Координаты крайних точек нагрузочной линии практически совпадают с данными примера 1. 7. Ток коллектора можно определять по выражению IК(Y)≈EК/(RК+Rэ).

Координаты точки покоя связаны с током покоя базы IОБ1=23мкА из примера1. 6.

IОК1=IОБ1·h211=23мкА ·80=1,84мА,

IОЭ1=(1+h211)IОК1/h211=(1+80) · 1,84мА/80=1,86мА,

UКЭ=ЕК – [RК ·IОК1 + IОЭ1Rэ]=12В – [1.8кОм ·1,84мА + 1,86мА ·1,2кОм]=6,45В.

Точка покоя А1 имеет координаты (6,45В; 1,84мА).

 

2.                  h21=300

 

Нагрузочная линия совпадает с другими. Определяем координаты точки покоя:

IОК2=IОБ2 · h212=6,97мкА ·300=2,09мА.

При большом h21  IОК ≈ IОЭ, тогда

UКЭ2 ≈ ЕК – IОК2 ·(RК + RЭ)= 12В – 2,09мА (1.8кОм + 1,2кОм) ≈ 5,7В.

Точка покоя А2 имеет координаты (5,7 В;  2,09мА).

 

На рис.1.12 изображены нагрузочные линии в плоскости выходных статических характеристик с точками покоя при различных h21 из примеров 1.6-- 1.8.

 

 

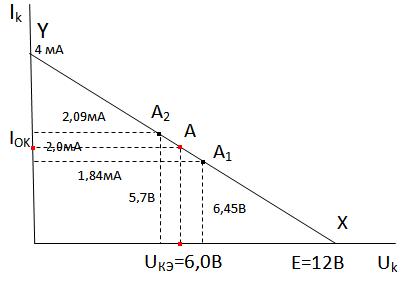
Рис.1.12 Нагрузочная линия и точки покоя по данным примеров 1.6 –1. 8.

Рисунки 1.10 и 1.12 являются наглядной иллюстрацией автоматического смещения. Видно, почему при большом изменении параметра транзисторов h21 ток покоя коллектора Iок меняется лишь на несколько процентов. В примере двукратное изменение h21 вызывает изменение тока покоя менее 10%. Из рис. 1.10 видно, что увеличение h21 вызывает уменьшение тока базы, и это существенно препятствует пропорциональному h21 увеличению тока покоя коллектора. Одновременно с этим изменением тока базы изменяется и напряжение база-эмиттер, которое задаётся пересечением нагрузочной прямой с нелинейной статической характеристикой. В примерах расчётов это не было учтено и смещение везде было принято UБЭ=0,7В.

Нет никакой гарантии, что полученный в расчётах ток покоя I ОБ, будет               соответствовать на входной характеристике транзистора именно смещению в 0,7В. Корректнее было бы учитывать связь тока базы и напряжения на базе транзистора, используя формулу Эберса-Молла. Однако в этом случае не только усложняется математика, но, главное, требуется ещё не менее трёх параметров транзистора и зависимость h 21 от тока базы. Получить необходимую информацию довольно трудно. Точность расчётов при этом возрастёт незначительно (если Вы не являетесь разработчиком интегральных микросхем). По этой причине можно считать используемую методику приемлемой в инженерной практике и учебном процессе. Правильность выбора U БЭ и h 21 легко проверить экспериментально.