Из-за больших значений полинома при x ~= -7 график полинома в той области, где расположены 4 последних корня, похож на линию. Поэтому нам следует рассмотреть именно эти промежутки. 
Теперь просто строим 2 графика полинома в наиболее «выгодных» промежутках с помощью функции subplot.
Единственная проблема, которая может возникнуть, это корни за выбранным интервалом. Т к функция plotнаносит все корни из вектора, маркеры будут располагаться вместе, где функция не построена. Поэтому необходимо избавиться от ненужных корней так же, как мы избавляемся от комплексных.
Вот как это выглядит
Первый подграфик

2 подграфик

Результат:

C) найти первые 3 производные и их вещественные корни.
Как обычно находим производные через функцию polyder, далее подставляя туда предыдущие производные

Корни производных:

D) построить графики полинома и его производных на четырех подграфиках друг под другом, обозначив на них точки, соответствующие вещественным корням
По идее пункт cдолжен был быть подготовительным к пункту d, но в силу особенностей моего полинома мне, потребуется сначала запустить программу с пунктом d’ для правильной работы пункта d.
Дело в том, что у производных есть корень около -7, который не дает нормально построить график в выбранном промежутке. Поэтому в пункте d мы добавляем условие, что корни должны быть больше -3, а также заранее находим значение предыдущей производной или полинома в точке корня.
Пункт d’. По сути тот же пункт с, но с указанными выше поправками

Теперь приступим
Строим как обычно в subplot - е
Для того, чтобы графики были читаемы, необходимо делать усечение
1 подграфик

2 подграфик
Некоторые точки экстремума находятся за гранью усечения. Им мы присваиваем значение границы усечения

Остальные подграфики стандартно:


Результат:

e) Сравнить координаты точек экстремумов, вычисленных двумя способами: - используя функцию поиска минимума, - как корень производной.
Присваиваем вектору значения корней поэлементно с помощью функции fminsearch
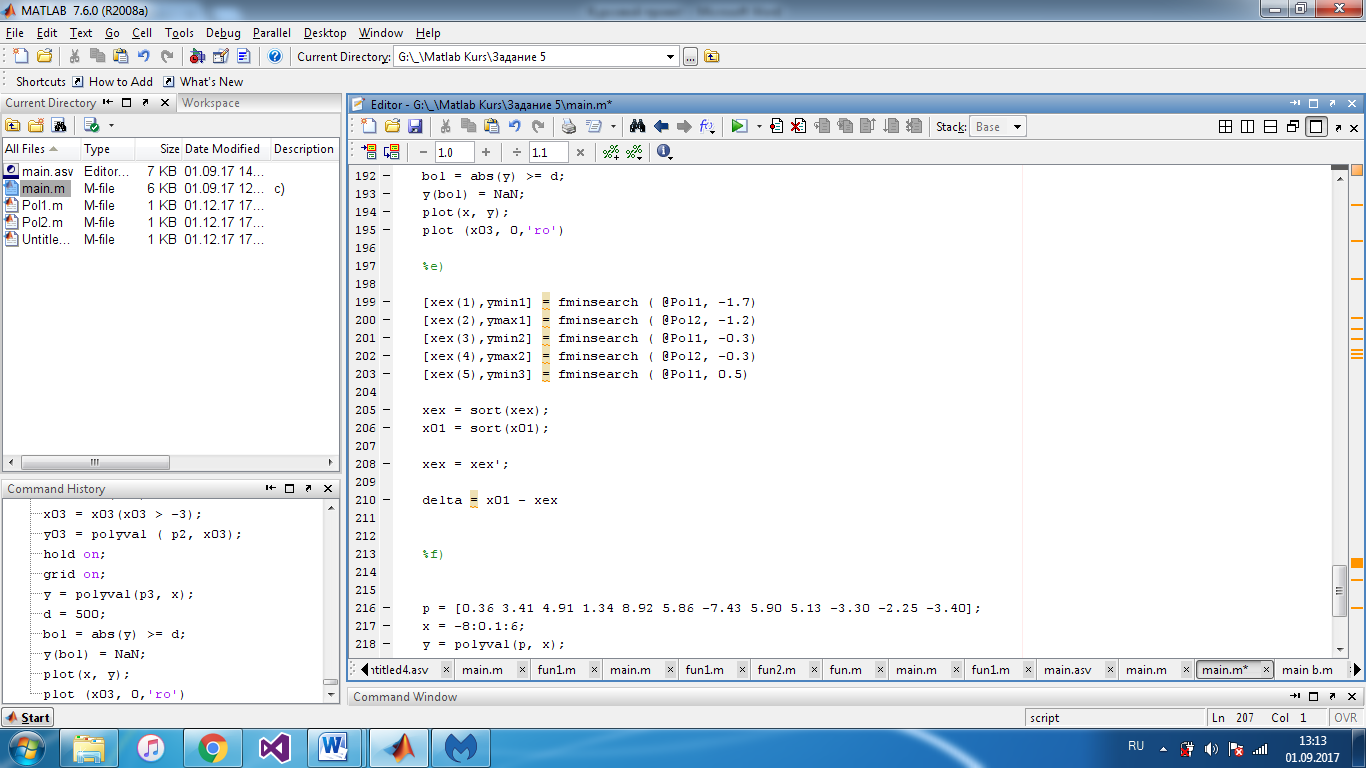
Получившиеся корни

Сортируем новый вектор с корнями и вектор с корнями, полученный в пункте ‘с’ с помощью функции sort

Получилось

хех – строка, поэтому транспонируем ее и находим разность
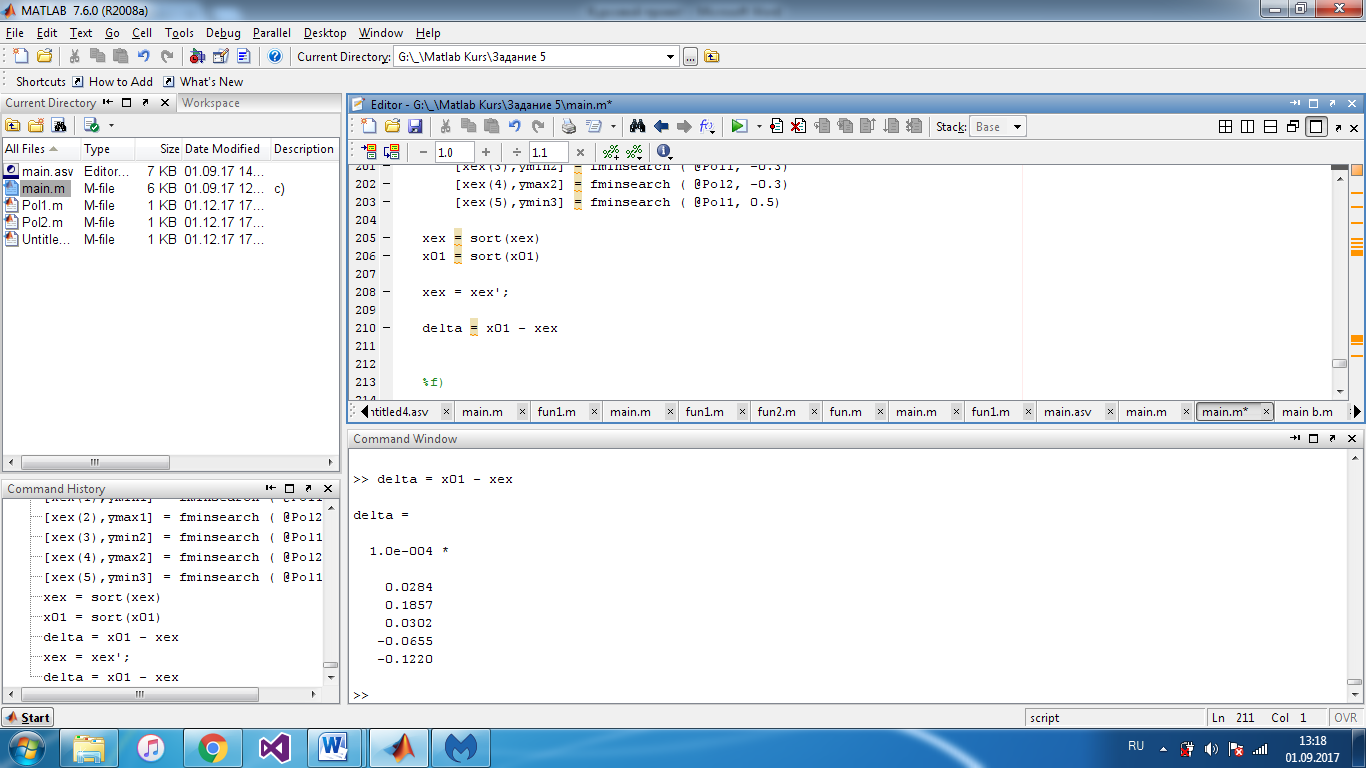

f) Внести случайное изменение, используя функцию rand, во второй коэффициент полинома (не более 5 %) и сравнить (вычислить относительную погрешность) каждого корня полинома






Решение задач алгебры
Для заданной системы линейных уравнений (файл СЛАУ-2017.pdf) получить решение тремя способами:
A) По правилу Крамера
Для начала мы должны создать 2 файла с матрицей и вектором в директории главного м-файла
После этого в начале программы считываем их с м-файла и записываем в переменные А и В
Матрицу В транспонируем в столбец

Находим определитель

Теперь в цикле мы присваиваем столбцам матрицы столбец В и ищем определители, корни и записываем их в вектор rootsa

Транспонируем вектор корней

Результат:





