Пределы:
Для того, чтобы найти пределы, необходимо задать х и другие переменные как символьные. Функцию можно красиво вывести для пользователя с помощью функции pretty. Еще надо задать символьную функцию и точку, в которой предел берется. После использовать функцию limit. И при необходимости функцию simpleдля упрощения. После ответ можно так же красиво вывести с помощью функции pretty.
В 424 номере ответ численный, поэтому функция simpleне нужна


Вот, что выводит функция pretty
Сама функция:

Ответ:

 .
.
В этом номере у нас появились буквенные коэффициенты. Задаем их символьно

Сама функция:

Ответ:

563

В данном примере возникли некоторые трудности. Дело в том, что в матлабе нет (или она мне неизвестна) готовой функции логарифма по выбранному нами основанию. Т е только натуральный, двоичный и десятичный. Поэтому прибегнем к хитрости.


Т к log2 может быть выражен как вещественное число, функция pretty выводит его именно так
Формула:

Ответ

Теперь нам нужно искать производные. Процесс схож с поиском пределов, только теперь не нужно задавать переменные символьно отдельно и вместо limitиспользуется функция diff, которая содержит функцию, символьное значение переменной и порядок производной.
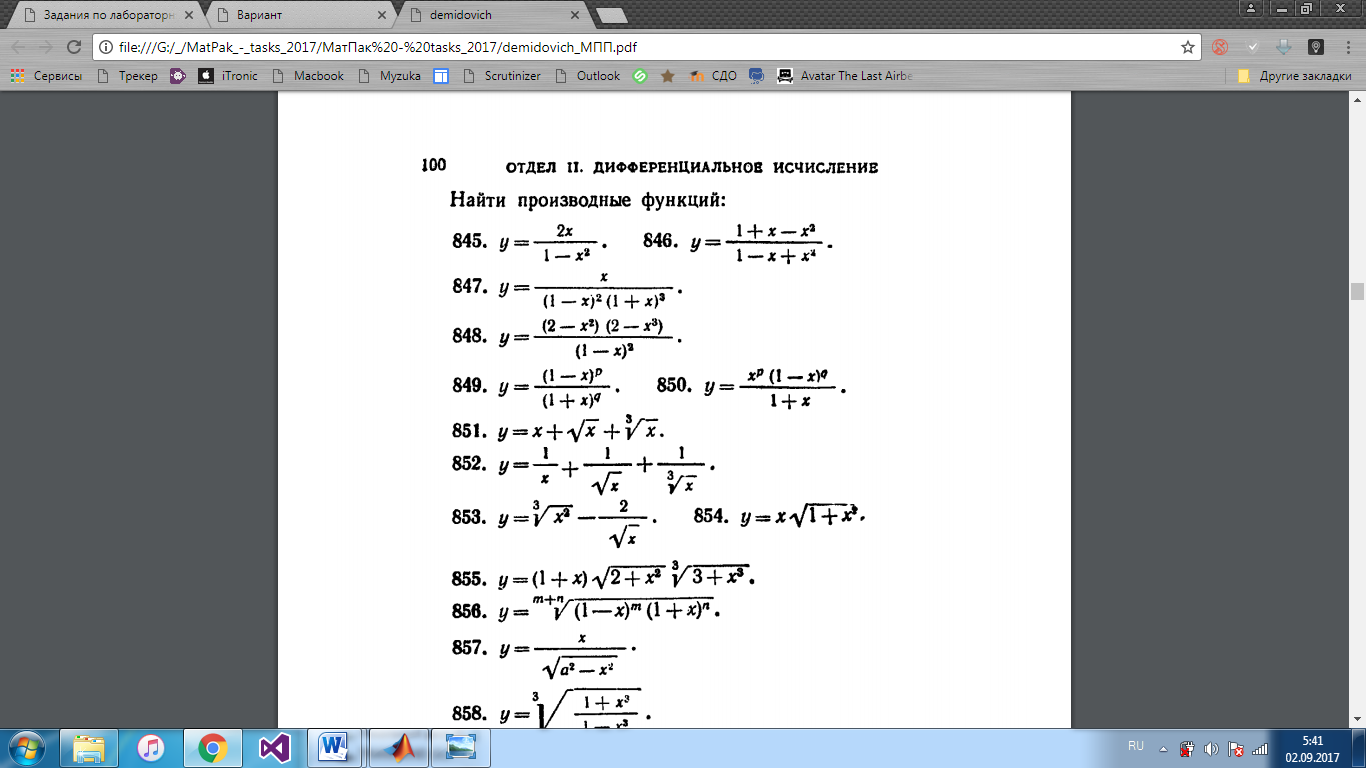

Функция:

Ответ:



Функция:

Ответ:


Тут у нас снова предел

Функция:
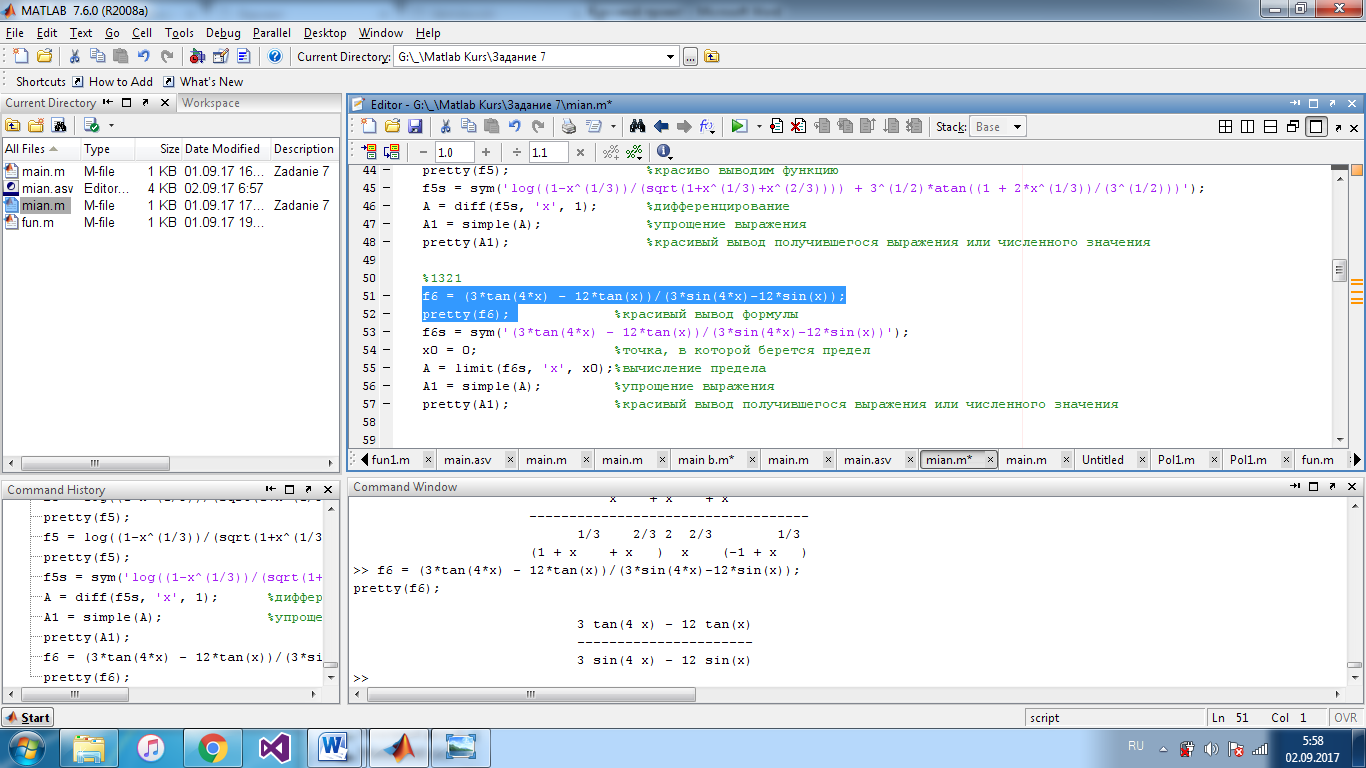
Ответ:

Решить кубическое уравнение аналитически и вычислить корни, используя функцию VPA. Сравнить их с посчитанными численно (без символьных вычислений) функциями roots и fzero.
Для того, чтобы решить кубическое уравнение символьно, необходимо сначала задать переменную (х) символьно. Далее найти корни с помощью команды solve, которая принимает функцию, написанную вручную и переменную, для которой нужно найти решения.
Далее полученный массив корней сортируем и с помощью функции vpa выводим с точностью до 15 знаков после запятой. Для этого также необходим задать formatlong в командной строке.
Символьно:


Результат:

Теперь найдем 1 вещественный корень с помощью функции fzero:
Для этого зададим нашу функцию в отдельном м-файле

Находим корень

Результат:

Осталось найти наши корни как корни полинома. Для этого определим вектор с коэффициентами полинома и найдем корни с помощью функции roots. Также следует не забыть отсортировать вектор корней.

Результат

Осталось сравнить все полученные значения
Сначала сравним корень, полученный через символьное решение с корнем, полученным через fzero

Разность:

Теперь сравним со значениями, полученными через roots

Результат:

Разложить заданную функцию в ряд Тейлора, удерживая разное число членов (2, 3, 4, 5). Вычислить коэффициенты полиномов и построить графики функции отрезка ряда Тейлора (не используя символьные вычисления) на симметричном (относительно точки разложения) интервале, с помощью функции plot.
Для того, чтобы разложить функцию по формуле Тейлора необходимо сперва задать аргумент функции символьно, после задать саму функцию, точку разложения и применить функцию taylor, в которой задается функция, количество элементов разложения, аргумент функции и точка разложения.
После как и в 1 пункте все это можно красиво вывести с помощью функции pretty.
Параллельно с разложением необходимо записывать коэффициенты в вектора, для построения этой же функции как полинома с помощью функцииsym2poly.

Вывод:
2 члена

3 члена

4 члена

5 членов

Теперь построим 4 графикa функции в subplot –e2-мяспособами и сравним их.
Построим в окрестности точки разложения.
Красным цветом – обычный способ
Синим – по Тейлору
Функцию задаем в отдельном м-файле




Построенные графики:

Здесь мы хорошо видим, что чем больше коэффициентов/элементов в разложении, тем наиболее точна зависимость, задаваемая формулой тейлора.
4 Используя функцию rand, построить систему линейных уравнений третьего порядка, имеющую единственное решение, с целыми коэффициентами из интервала [ - 9, 9 ]. Решить систему линейных уравнений аналитически, применяя функцию solve и обращая матрицу функцией inv. Решить эту же систему численно без символьных вычислений. Сравнить результаты, удерживая 10 значащих цифр.
Сперва задаем символьные переменные.
Далее заполняемматрицу A с помощью функции random. В эту функцию задаются команда ’unid', что обеспечивает равномерное заполнение, максимальное число и размеры матрицы. Эта функция генерирует числа от 0 до определенного значения, поэтому для того, чтобы задать диапазон от -9 до 9 необходимо генерировать числа от 1 до 19, а потом из них вычесть 10.

Далее задаем уравнения системы

Теперь мы можем решить эту систему символьным методом через функцию solveи вывести с точностью до 15 цифр с помощью функции vpa. Также нужно решить через обратную матрицу.

Результат:
Символьным

Через обратную

Осталось найти погрешность и вывести, удерживая 10 значащих цифр

Результат







