Методика (с примером) решения задач на тему: Электрические цепи с параллельным соединением активного, емкостного и индуктивного сопротивлений.
Цель: рассчитать напряжения, токи на элементах цепи. Построить диаграмму напряжений и токов.

Теория.
Для такой цепи характерно то, что электроприемники, соединенные параллельно, находятся под общим напряжением. Ток каждой ветви определяется по закону Ома: I 1 = U / Z 1,где Z 1 = √ R 1 2 + XL 1 2, I2 = U /Z2, где Z2 =√ R 2 2 + XC 2 2.
Углы сдвига фаз φ1 и φ2 между током и напряжением каждой ветви определяются с помощью тригонометрических функций:
cos φ1= R1 / Z1 и sin φ1= XL1 / Z1, cos φ2= R2 / Z2 и sin φ2= - XC2 / Z2.
Угол сдвига фаз обязательно следует проверять по синусу во избежание потери знака угла (cos является четной функцией), но находить его тоже нужно. Он потребуется в дальнейшем расчете цепи.
Общий ток цепи следует из I закона Кирхгофа, он равен сумме токов ветвей:
I = I1 + I2.
Векторная диаграмма этих токов:

Общий суммарный или результирующий ток можно найти не только графически (диаграмма строится в масштабе), но и математически, на основании теоремы Пифагора: I = √ Ia 2 +I p 2, где I a – проекция вектора общего тока на вектор напряжений, она называется активной составляющей общего тока, где Iр – проекция вектора общего тока на линию, перпендикулярную линии напряжения, она называется реактивной составляющей общего тока. Из диаграммы видно, что Iа= Iа1 + Iа2, Iр=IL1 - IС2.
В этих формулах: Iа1 и Iа2 - активные составляющие токов первой и второй ветви.
I L1 - реактивные составляющие тока первой ветви. Она носит индуктивный характер и поэтому взята знаком “плюс”.
Iс2 - реактивные составляющие тока второй ветви. Она носит емкостной характер и поэтому взята знаком “минус”.
Введем формулу общего тока: I =√ (Ia1 + Ia 2) 2 + (IL1 - I C2) 2
Значения составляющих токов ветвей можно определять по формулам:
I а1 = I 1 cos φ1; I а2 = I 2 cos φ2; IL 1 = I 1 sin φ1; IC 2 = I 2 sin φ2.
Активная мощность цепи равна арифметической сумме активных мощностей ветвей: Р = Р1 + Р2, где Р1 = U I 1 cos φ1 или Р1 = I 1 2 R 1, Р2 = U I 2 cos φ2 или Р2 = I 2 2 R 2.
Реактивная мощность цепи равна алгебраической сумме реактивных мощностей ветвей: Q =QL1 - QC2, где QL1= U I1 sin φ1 или QL1 = I12 Х L1, QС1= U I2 sin φ2 или
QС2 = I22 Х С2.
Активную и реактивную мощность можно найти и так: Р = UI cos φ или
Q = U I sin φ, г де cos φ = (I а1 + I а2) / I, sin φ = (IL 1 - IC 2) / I,
cos φ и sin φ используют также для определения угла сдвига фаз между общим током и напряжением.
Полная мощность цепи: S =U I или S = √ P 2 + Q 2
Угол сдвига фаз между общим током и напряжением можно определять и из выражений: cos φ = Р / S, sin φ = Q / S
Пример задачи параллельного соединения
Дано: U = 540 B, R1 = 28,8 Oм, XL1 =21,6 Oм, R2 = 45 Oм, XC3=20 Oм.
Определить: I1, I2, I3, I, P, Q, S, cos φ, построить векторную диаграмму токов в масштабе.
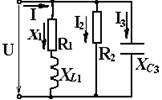
Решение.
1.Полное сопротивление первой (левой) ветви Z1=√ R 1 2 + XL 1 2 = = √ 28,82 +21,6 2 = 36 Oм.
Косинус и синус угла сдвига фаз φ1 между напряжением и током левой ветви:
cos φ1 = R1 / Z1 = 28,8 / 36= 0,8; sin φ1 =X L1 / Z1 = 21,6 / 36 = 0,6
Ток в первой ветви I1 = U / Z1 = 540 / 36 = 15 A.
Активная и реактивная составляющая тока первой ветви:
Iа1 = I1 cos φ1 = 15 · 0,8 =12 A; IL1 = I1 sin φ1 = 15 · 0,6 = 9 A
2.Во второй (средней) ветви дано только активное сопротивление, поэтому ее ток I2 = I2a = U / R2 = 540 В / 45 Ом = 12 A.
Он совпадает по фазе с напряжением и носит активный характер, угол сдвига фаз между этим током и напряжением φ2 = 0.
Реактивная составляющая тока в этой ветви отсутствует I2P = I2 sin φ2 = 12 · 0= 0
3.В третьей (правой) ветви дано только емкостное сопротивление, поэтому ее ток I3 = I C3 = U/XС3= 540 В / 20 Ом = 27 A.Этот ток опережает напряжение на угол φ3 = - 90°.
Активная составляющая тока этой ветви равна нулю I a3 = I3 cos φ3 = 27 cos (- 90◦) = 0
4. Определяем ток в неразветвленной части цепи:
I = √ (I a1 + I a 2) 2 + (I L1 - I C3 ) 2 = √ (12+12)2+(9-27)2 = 30 A.
5.Определяем коэффициент мощности всей цепи:
cos φ = (I a1 + I a 2) / I =(12+12)/ 30=0,8
6.Угол сдвига фаз находим по синусу во избежание потери знака угла (косинус является четной функцией) sin φ =(I L 1 - I C 3) / I = (9- 27) / 30 = - 0,6.
Используя таблицу или калькулятор, находим угол φ = -36° 52´
7.Определяем активную мощность цепи:
Р = UI cos φ = 540·30·0,8 = 12960 Bт или Р = Р1 + Р2, где Р1 = UI1 cos φ1 или
Р 1 = I12R1 , Р 2 = UI2, или Р 2 = I22R2.
8.Реактивная мощность цепи равна Q = U I sin φ = 540 · 30 · (- 0,6)= -9720 вар
Знак “минус” говорит о преобладании емкостного характера нагрузки над индуктивным. Эту мощность можно найти и так:
Q =QL1 - Q C3, где QL1= U I1 sin φ1 или QL1 = I12 Х L1, QС3= U I3 sin φ1 или QС3 = I32 Х C 3
Активную и реактивную мощность можно найти и так: Р = UI cos φ,
Q= U I sin φ
9.Определяем полную мощность цепи S = U I =16200 ВА. Эту мощность можно найти и так: S = √ P 2 + Q 2.






