В электрической цепи, помимо активного сопротивления, могут быть включены одновременно два реактивных элемента: индуктивность L и ёмкость С. Работа цепи в этом случае будет зависеть от того, какой из реактивных элементов преобладает.
Как известно, элементы L и С обладают противоположными свойствами. В зависимости от того, какой из двух реактивных элементов преобладает, цепь будет вести себя как активно-индуктивная (действие индуктивности сильнее) или активно-ёмкостная (сильнее действие ёмкости). Действие более "слабого" реактивного элемента буден нейтрализовано действием более "сильного" элемента.
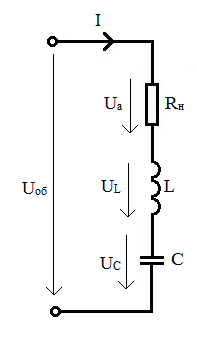
Рис. 61. Последовательное соединение элементов RLC
Чтобы понять процессы, происходящие в такой цепи, рассмотрим векторную диаграмму для случая преобладания индуктивности (рис. 62). Преобладание индуктивности возникает, если индуктивное сопротивление XL больше ёмкостного сопротивления XC.
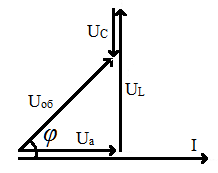
Рис. 62. Векторная диаграмма для цепи с последовательным соединением
элементов RLC. Индуктивность в цепи преобладает
В последовательной цепи переменного тока, общее напряжение, приложенное к цепи, равно векторной сумме напряжений на элементах, входящих в цепь.
Прежде всего, проводится вектор тока I, одинаковый во всех элементах последовательной цепи. Затем, последовательно строятся векторы напряжений на элементах цепи: Uа, UL, и UC. При построении векторов напряжений учитываем их сдвиг по фазе относительно тока.
На диаграмма можно выделить прямоугольный треугольник напряжений, в котором гипотенузой является напряжение Uоб, а катетами являются напряжение Uа и разность напряжений (UL-UC).
По теореме Пифагора, для прямоугольного треугольника:
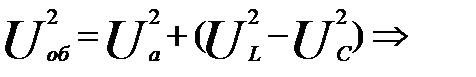
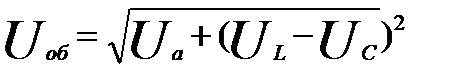
От треугольника напряжений можно перейти к треугольнику сопротивлений и к треугольнику мощностей. Если стороны треугольника напряжений, в масштабе, поделить на ток, то получится треугольник сопротивлений. Если же стороны треугольника напряжений умножить на ток, получим треугольник мощностей.
Используя теорему Пифагора, из треугольника сопротивлений и треугольника мощностей можно записать формулы для сопротивлений и мощностей:
полное сопротивление цепи 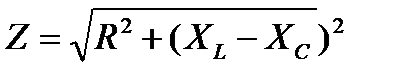 (Ом);
(Ом);
полная мощность 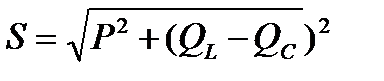
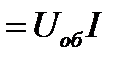 (ВА).
(ВА).
Все рассмотренные формулы записаны для случая, когда в цепи преобладает индуктивность. Однако, они будут справедливы и в случае, когда преобладает ёмкость. При этом, в скобке, входящей в формулу, будет получаться отрицательное значение. Этот факт не имеет значения и не влияет на результат вычисления.
Векторная диаграмма цепи, в которой преобладает ёмкость показана на рис. преобладает емкость, то диаграмма примет вид, показанный на рис. 63. Преобладание ёмкости возникает в случае, когда ёмкостное сопротивление XC больше индуктивного сопротивления XL.
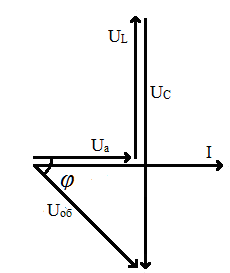
Рис. 63. Векторная диаграмма для цепи с последовательным соединением
элементов RLC. В цепи преобладает ёмкость
Для построения диаграммы в масштабе смотри раздел «Графическое изображение синусоидальных величин».
Пример 15. Последовательное соединение элементов RLC в цепи синусоидального тока.
В цепи последовательно соединены элементы: активное сопротивление R = 12 Ом, индуктивное сопротивление ХL = 32 Ом и емкостное ХС = 16 Ом. Общее напряжение, приложенное к цепи Uоб=120 В.
Определить ток в цепи, напряжение на каждом элементе, а также активную, реактивную и полную мощность.
Решение
Полное сопротивление цепи
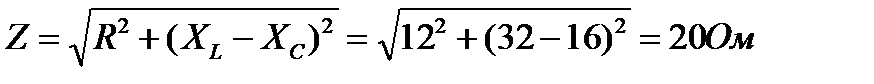 .
.
По закону Ома находим ток в цепи:
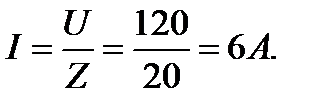
Напряжения на элементах цепи:
на резисторе Uа= I*R;
на индуктивности UL=I*XL;
на ёмкости UC=I*XC.
Мощности, выделяющиеся в цепи:
активная, выделяющаяся в сопротивлении,
Р = I2 · R=36 · 12 = 432 Вт;
реактивная, выделяющаяся в реактивных элементах,
Q = I2 · ( XL- XC) = 62 · 16 = 576 Вар;
полная, выделяющаяся в цепи в целом
S =UI = 120 · 6 = 720 ВА.
При построении векторной диаграммы к задаче по рис.63 или 63 нужно, прежде всего выбрать масштаб. Например 20В в одном см. Он одинаков для всех напряжений. Также, нужно выбрать масштаб для тока, например 1A в см.






