(цепочка RL)
Ранее была рассмотрена идеальная катушка индуктивности, где мы учитывали только один параметр – индуктивность катушки. Для реальной катушки индуктивности приходится учитывать не только её индуктивность L, но и сопротивление R – провода, которыми она намотана. К реальным катушкам индуктивности относятся, например, обмотки трансформаторов и электродвигателей.
На схеме реальная катушка индуктивности изображается последовательным соединением элементов R и L (рис. 57). На каждом из этих элементов действует напряжение, обозначенное на рис. 57 стрелкой. На сопротивлении действует активное напряжение Ua, а на индуктивности – индуктивное напряжение UL.
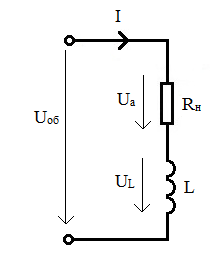
Рис. 57. Последовательное соединение элементов R и L
Известно, что при последовательном соединении элементов цепи общее напряжение равно сумме напряжений на этих элементах.
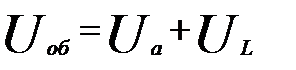
Сумма эта векторная, арифметически суммировать напряжения в цепях переменного тока нельзя. Складывать векторы можно только по рассмотренным выше правилам сложения векторов.
Для понимания работы электрической цепи переменного тока, прежде всего, необходимо построить векторную диаграмму. Для рассматриваемой цепи векторная диаграмма будет иметь вид, показанный на рис. 58.
В последовательных цепях построение диаграмм начинается с вектора тока, так как он одинаков во всех элементах цепи.
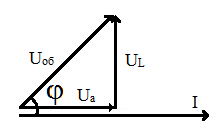
Рис. 58. Векторная диаграмма для цепи с последовательным соединением
элементов R и L
Затем проводим вектор напряжения на активном сопротивлении. Он совпадает по фазе с током в цепи.
К концу вектора Ua пристраиваем вектор напряжения UL на индуктивности. Он направлен вверх, поскольку напряжение на индуктивности опережает ток на 90 градусов. Для построения диаграммы в масштабе смотри раздел Графическое изображение синусоидальных величин.
Общее напряжение, приложенное к цепи является суммой этих двух векторов. Суммируя напряжения Ua и UL, проведём вектор суммарного напряжения Uоб из начала вектора Ua к концу вектора UL.
Из диаграммы следует, что ток в цепи отстаёт по фазе от приложенного к цепи напряжения Uоб на угол φ меньше 90 градусов.
Три напряжения на векторной диаграмме образуют треугольник напряжений. В этом прямоугольном треугольнике гипотенузой является напряжение Uоб, а катетами – напряжения Ua и UL.
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.
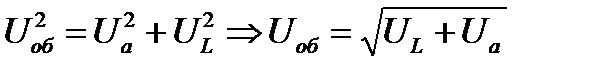
(Здесь и далее, в формулах, стрелка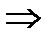 
заменяет слово "следовательно") По закону Ома, ток равен напряжению, делённому на сопротивление цепи:
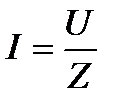, где
Z– полное сопротивление в цепи, которое учитывает совместное действие активного R и индуктивного XL сопротивлений.
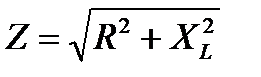
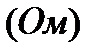
Цепь содержит активный и реактивный компоненты. В резисторе выделяется активная мощность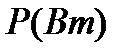 
. В катушке выделяется реактивная мощность 
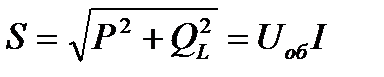. Во всей цепи выделяется полная мощность S, измеряемая в вольт-амперах (ВА).
(ВА)
Пример 13. Реальная катушка в цепи синусоидального тока.
В сеть с напряжением 50 В и частотой 50 Гц включена реальная катушка с индуктивностью L = 0,0127 Гн. и активным сопротивлением R = 3 Ом. Определить ток, напряжения на элементах цепи, активную, реактивную и полную мощности катушки.
Решение
Реальная катушка индуктивности помимо индуктивности L обладает, также, сопротивлением провода R, которым она намотана. На схеме реальная катушка изображается последовательным соединением сопротивления R и индуктивности L.
Индуктивное сопротивление катушки
XL=2πfL = 2 · 3,14 · 50 · 0,0127 = 4Ом.
Полное сопротивление цепи
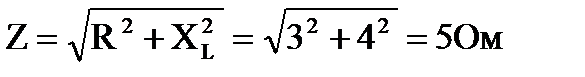
Ток определяется напряжением, приложенным к цепи, и её полным сопротивлением
I = Uоб /Z = 50/5 = 10 А.
Напряжения на активном и индуктивном сопротивлениях, входящих в цепь, определим по закону Ома:
напряжение на активном сопротивлении: Ua= I·R== 10 · 3 = 30 В;
напряжение на индуктивном сопротивлении: UL=I · XL = 10 · 4 = 40 В.
Активная, реактивная и полная мощности, выделяющиеся в элементах цепи:
Р = Uа · I = 30 · 10 = 300 Вт;
QL = UL · I= 40 · 10 = 400 вар:
S = Uоб· I = 50 · 10 = 500 BА.
