Конденсатор представляет собой две металлические пластины (обкладки), разделённые диэлектриком. Если приложить к конденсатору постоянное напряжение, на его обкладки поступит электрический заряд, как показано на рис. 53. Полученный заряд может сохраняться на обкладках долгое время. Заряды со знаком "плюс" и "минус" притягиваются друг к другу и не могут уйти с обкладок. В то же время они не могут и соединиться, нейтрализовав друг друга, т.к. этому препятствует диэлектрик (изоляция) между обкладками. Таким образом, конденсатор это устройство, предназначенное для накопления и хранения электрического заряда. (Поскольку изоляция между обкладками неидеальна, рано или поздно конденсатор разрядится – потеряет заряд)
Рис. 53. Конденсатор хранит заряд на своих обкладках
Постоянный ток не может проходить через конденсатор. Этому препятствует диэлектрик между обкладками.
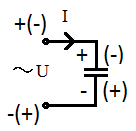
Рис. 54. В цепи переменного напряжения через конденсатор протекает ток.
Как ни странно, переменный ток может проходить в цепи с конденсатором, несмотря на наличие изоляции между обкладками.
При переменном напряжении конденсатор, при смене полупериода, вынужден постоянно перезаряжаться. При этом меняется полярность и величина заряда на обкладках конденсатора (см. рис. 54).
В положительный полупериод синусоиды на верхнюю обкладку конденсатора поступает положительный заряд, а на нижнюю – отрицательный.
В отрицательный полупериод (его полярность показана в скобках) заряд на обкладках меняется на противоположный.
При работе в цепях синусоидального тока конденсатор постоянно перезаряжается. В проводниках, подводящих напряжение к конденсатору, происходит перемещение заряда. Это означает, что в цепи протекает ток.
Вместо термина "конденсатор" часто используется термин "емкость". Это слово имеет в электротехнике два значения:
- параметр конденсатора, характеризующий его величину заряда, который он способен накапливать;
- собственно конденсатор.
Конденсатор оказывает сопротивление проходящему току. Это сопротивление называется ёмкостным, обозначается XCи определяется по формуле:
, где:
f - частота приложенного напряжения;
С - ёмкость конденсатора (Фарад).
Ёмкостное сопротивление зависит от частоты. С ее увеличением емкостное сопротивление уменьшается. Соответственно, ток в цепи с конденсатором увеличивается:
В конденсаторе ток опережает напряжение на угол 
радиан (90 градусов).
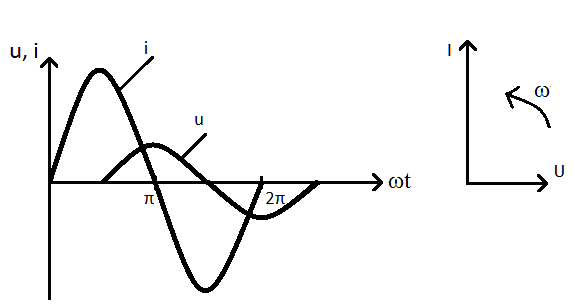
Рис. 55. В конденсаторе ток опережает по фазе приложенное напряжение
Конденсатор, как и катушка индуктивности, относится к реактивным элементам. В реактивных элементах происходит обратимое преобразование энергии. Конденсатор сначала забирает энергию от источника напряжения, накапливает энергию в своём электрическом поле, а затем отдает ее генератору. Затем процесс повторяется.
В конденсаторе выделяется реактивная мощность:
,
Пример 12. Идеальный конденсатор в цепи синусоидального тока.
К конденсатору емкостью С = 63,7 мкФ приложено напряжение u=141sin314t, В. Определить действующее значение тока и реактивную мощность конденсатора.
Решение.
Идеальный конденсатор обладает только одним параметром – ёмкостью. Влияние сопротивления изоляции между обкладками не учитывается.
В условии задачи приведено уравнение напряжения, действующего на входе цепи, имеющее вид: u = Um sinwt. Из этого уравнения можно узнать амплитуду приложенного напряжения Um =141В и угловую частоту w = 314рад/сек.
Зная амплитуду Um, приложенного напряжения, находим действующее значение напряжения U=Um/1,41=141/1,41=100B.
Зная, что угловая частота w = 2pf, находим частоту приложенного к конденсатору напряжения f = w/2p =314/6,28=50Гц.
Емкостное сопротивление конденсатора
Xc=1/2pfC=1 / 6,28·50·63,7·10-6=50 Ом.
В этой формуле ёмкость конденсатора выражена в фарадах, для чего, предварительно, был сделан перевод ёмкости конденсатора из микрофарад, приведённых в условии задачи, в фарады. Приставка "микро" обозначает одну миллионную долю, следовательно:
63,7мкФ = 63,7/1000000 Ф = 63,7·10-6 Ф.
Ток в цепи, по закону Ома
I = U /Xс = 100/50 = 2 А.
Реактивная мощность
Qc = UI = 100 • 2 = 200 вар.
